这是三种线性时间复杂度的排序算法,它们是用运算而不是比较来确定排序顺序的
一、基数排序
1.简介
它一种与其他排序算法完全不同的排序方法,其他的排序算法都是通过关键字之间的比较和移动来完成的,而它是采用一种多关键字的思想。
多关键字的思想:给定一组数据,我可以先按个位的大小对所有数进行排序,然后再按十位进行排序,一直到最高位,这样就可以使整组数据变得有效,这样从最低位开始的方法称为最低位优先
2.图解过程

经过一次放置和回收,得到的序列已经按个位有序了,接下来按照次低位再次进行放置和回收。

由此可以看出,如果一组序列中最大的数为两位数,则需要两次的分配和收集,整个分配收集的次数与最大数的位数有关
基数排序需要两个辅助空间,一个是0~9号桶,另一个是计算定位的数组,定位数组是干什么的呢?就是记录每个桶中的数据待会要放回原数组的哪个位置。

def radixSort(number: Array[Int], d: Int): Unit = { //d表示最大的数有多少位
var k = 0
var n, m = 1
//控制键值排序依据在哪一位
val temp = Array.ofDim[Int](10, number.length)
//数组的第一维表示可能的余数0-9
val order = new Array[Int](10) //数组orderp[i]用来表示该位是i的数的个数
while (m <= d) {
for (i <- number.indices) {
val lsd = (number(i) / n) % 10
temp(lsd)(order(lsd)) = number(i)
order(lsd) += 1
}
var i = 0
while (i < 10) {
if (order(i) != 0) {
var j = 0
while (j < order(i)) {
number(k) = temp(i)(j)
k += 1
j += 1
}
}
order(i) = 0
i += 1
}
n *= 10
k = 0
m += 1
}
}
基数排序的时间复杂度可以理解为O(d*n),d为序列中最大的位数,适用于n值很大,但是关键字较小的序列。
二、桶排序
1.概念
桶排序将[0,1)区间划分为n个相同的大小的子区间,这些子区间被称为桶。然后将n个输入元素分别放入各自的桶中。因为输入时均匀独立的,所以一般不会有很多数同时落在一个桶中的情况。这样,我们想对各个桶中的数据进行排序,然后遍历每个桶,按照次序把各个桶中的元素列出来即可
2.特性说明
1》. 桶排序的时间复杂度通常是O(N+N*logM),其中,N表示桶的个数,M表示桶内元素的个数(这里,M取的是一个大概的平均数,这也说明,为何桶内的元素尽量不要出现有的很多,有的很少这种分布不均的事情,分布不均的话,算法的性能优势就不能最大发挥)。
2》. 桶排序是稳定的(是可以做到平衡排序的)。
3》. 桶排序,在内存方面消耗是比较大的,可以说其时间性能优势是由牺牲空间换来的。
桶排序,在大数据量的情况下排序,比快速排序还要快。若待排序的数据元素个数比较少,桶排序的优势就不是那么明显了,因为桶排序就是基于分而治之的策略,可以将数据进行分布式排序,充分发挥并行计算的优势。
3.步骤
1》.找出待排序数组中的最大值max、最小值min
2》.我们使用 动态数组ArrayList 作为桶,桶里放的元素也用 ArrayList 存储。桶的数量为(max-min)/arr.length+1
3》.遍历数组 arr,计算每个元素 arr[i] 放的桶
4》.每个桶各自排序
5》.遍历桶数组,把排序好的元素放进输出数组
4.实现
def bucketsort(inputData: ArrayBuffer[Int], max: Int): ArrayBuffer[Int] = {
var buckets = new Array[Int](max)
for (i <- inputData.indices) //计数
buckets(inputData(i)) = buckets(inputData(i)) + 1
var j = 0
for (i <- 0 until max)
while (buckets(i) > 0) {
inputData(j) = i
j = j + 1
buckets(i) = buckets(i) - 1
}
buckets = null
inputData
}
三、计数排序
1.优势
计数排序是桶排序的一种特殊情况,可以把计数排序当成每个桶里只有一个元素的情况,它是一个非基于比较的排序算法,它的优势在于在对一定范围内的整数排序时,它的复杂度为Ο(n+k)(其中k是整数的范围),快于任何比较排序算法。
2.思想
对于一个输入数组中的一个元素x,如果这个数组中比x小的元素有n个,那么我们就可以直接把x放到(n+1)的位置上。这就是计数排序的基本思想,类似于哈希表中的直接定址法,在给定的一组序列中,先找出该序列中的最大值和最小值,从而确定需要开辟多大的辅助空间,每一个数在对应的辅助空间中都有唯一的下标。
基于这个思想,计数排序的一个主要问题就是如何统计数组中元素的个数。再加上输入数组中的元素都是0-k区间的一个整数这个条件,那么就可以通过另外一个数组的地址表示输入元素的值,数组的值表示元素个数的方法来进行统计。
下面给出统计数组元素都是0-k区间的整数的数组中各个元素个数的方法。
- 找出序列中最大值和最小值,开辟Max-Min+1的辅助空间
- 最小的数对应下标为0的位置,遇到一个数就给对应下标处的值+1,。
- 遍历一遍辅助空间,就可以得到有序的一组序列
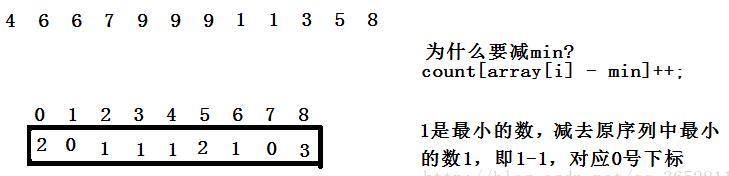
3.算法分析:
计数排序是一种以空间换时间的排序算法,并且只适用于待排序列中所有的数较为集中时,比如一组序列中的数据为0 1 2 3 4 999;就得开辟1000个辅助空间。
时间复杂度
计数排序的时间度理论为O(n+k),其中k为序列中数的范围。
不过当O(k)>O(n*log(n))的时候其效率反而不如基于比较的排序(基于比较的排序的时间复杂度在理论上的下限是O(n*log(n)), 如归并排序,堆排序)
4.代码实现
def Countingsort(inputData: ArrayBuffer[Int], k: Int): Array[Int] = {
//k表示有所输入数字都介于0到k之间
val temp = new Array[Int](k)
// 临时存储区
val outdata = new Array[Int](inputData.length)
val len = temp.length
for (i <- 0 until len) {
// 初始化
temp(i) = 0
}
for (i <- inputData.indices) {
temp(inputData(i)) = temp(inputData(i)) + 1
}
for (i <- 1 until len) {
temp(i) = temp(i) + temp(i - 1)
}
// 把输入数组中的元素放在输出数组中对应的位置上
var n = inputData.length - 1
while (n >= 0) {
// 从后往前遍历
outdata(temp(inputData(n)) - 1) = inputData(n)
temp(inputData(n)) = temp(inputData(n)) - 1
n = n - 1
}
outdata
}