一:传统神经网络存在的问题
- 权值太多,计算量太大
- 权值太多,需要大量样本进行训练
二:卷积神经网络(CNN)
CNN通过感受野和权值共享减少了神经网络需要训练的参数个数。

三:池化
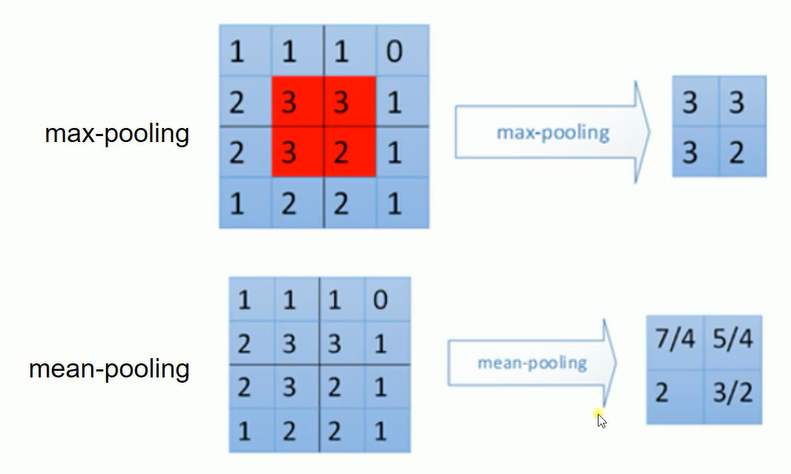
四:卷积操作


五:CNN结构
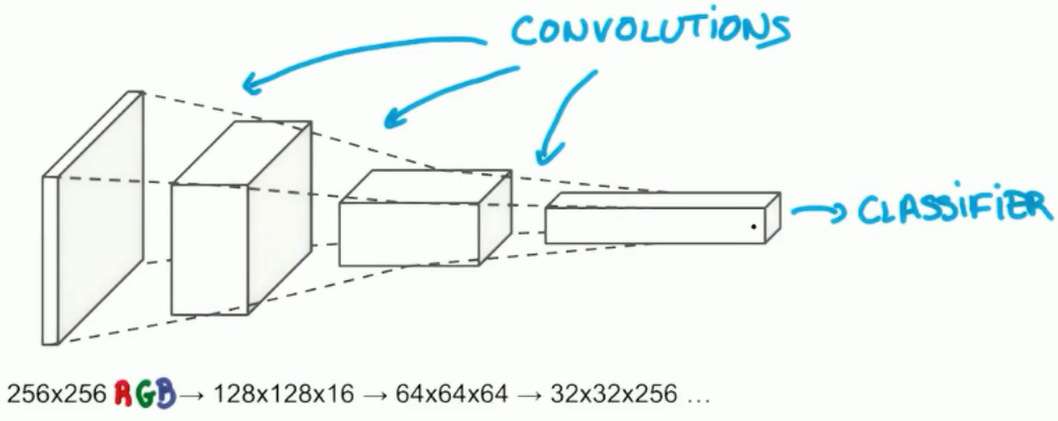
六:基于卷积神经网络的手写数字识别
import tensorflow as tf from tensorflow.examples.tutorials.mnist import input_data # 载入数据集 mnist=input_data.read_data_sets('MNIST_data',one_hot=True) # 每个批次的大小 batch_size=100 # 计算一共有多少个批次 n_batch=mnist.train.num_examples//batch_size # 初始化权值 def weight_variable(shape): initial=tf.truncated_normal(shape,stddev=0.1)# 生成一个截断的正态分布 return tf.Variable(initial) # 初始化偏置 def bias_variable(shape): initial=tf.constant(0.1,shape=shape) return tf.Variable(initial) # 卷积层 def conv2d(x,W): # x input tensor of shape (batch,in_height,in_width,in_channels) # W 相当于滤波器,卷积盒 # W filter/kernel tensot of shape [filter_height,filter_width,in_channels,out_channels] # strides[0]=strides[3]=1;strides[1]代表x方向的步长,strides[2]代表y方向的步长 # padding:A string from:'SAME','VALID' return tf.nn.conv2d(x,W,strides=[1,1,1,1],padding='SAME') # 二维的卷积操作 # 池化层 def max_pool_2x2(x): # ksize[1,x,y,1] # ksize表示窗口大小 return tf.nn.max_pool(x,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME') # 定义两个placeholder x=tf.placeholder(tf.float32,[None,784]) # 28*28 y=tf.placeholder(tf.float32,[None,10]) # 改变x的格式转为4D的向量[batch,in_height,in_width,in_channels] x_image=tf.reshape(x,[-1,28,28,1]) # 初始化第一个卷积层的权值和偏置 W_conv1=weight_variable([5,5,1,32])# 5*5的采样窗口,32个卷积核从1个平面抽取特征 b_conv1=bias_variable([32]) # 每一个卷积核一个偏置值 # 吧x_image和权值向量进行卷积,再加上偏置值,然后应用于relu激活函数 h_conv1=tf.nn.relu(conv2d(x_image,W_conv1)+b_conv1) h_pool1=max_pool_2x2(h_conv1) # 进行max-pooling # 初始化第二个卷积层的权值和偏置 W_conv2=weight_variable([5,5,32,64])# 5*5的采样窗口,64个卷积核从32个平面抽取特征 b_conv2=bias_variable([64]) # 每一个卷积核一个偏置值 # 把h_pool1和权值向量进行卷积,再加上偏置值,然后应用于relu激活函数 h_conv2=tf.nn.relu(conv2d(h_pool1,W_conv2)+b_conv2) h_pool2=max_pool_2x2(h_conv2) # 进行max-pooling # 28*28的图片第一次卷积后还是28*28,第一次池化后变为14*14 # 第二次卷积后为14*14,第二次池化后变为7*7 # 经过上面操作后得到64张7*7的平面 # 初始化第一个全连接层的权值 W_fc1=weight_variable([7*7*64,1024]) # 上一场有7*7*64个神经元,全连接层有1024个神经元 b_fc1=bias_variable([1024]) # 1024个节点 # 吧池化层2的输出扁平化为1维 h_pool2_flat=tf.reshape(h_pool2,[-1,7*7*64]) # 求第一个全连接层的输出 h_fc1=tf.nn.relu(tf.matmul(h_pool2_flat,W_fc1)+b_fc1) # keep_prob用来表示神经元的输出概率 keep_prob=tf.placeholder(tf.float32) h_fc1_drop=tf.nn.dropout(h_fc1,keep_prob) # 初始化第二个全连接层 W_fc2=weight_variable([1024,10]) b_fc2=bias_variable([10]) # 计算输出 prediction=tf.nn.softmax(tf.matmul(h_fc1_drop,W_fc2)+b_fc2) # 交叉熵代价函数 cross_entropy=tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(labels=y,logits=prediction)) # 使用AdamOptimizer进行优化 train_step=tf.train.AdamOptimizer(1e-4).minimize(cross_entropy) # 结果存放在一个布尔列表中 correct_prediction=tf.equal(tf.argmax(prediction,1),tf.argmax(y,1)) # argmax返回一维张量中最大的值所在的位置 # 求准确率 accuracy=tf.reduce_mean(tf.cast(correct_prediction,tf.float32)) with tf.Session() as sess: # 初始化所有变量 sess.run(tf.global_variables_initializer()) for epoch in range(21): for batch in range(n_batch): batch_xs,batch_ys=mnist.train.next_batch(batch_size) sess.run(train_step,feed_dict={x:batch_xs,y:batch_ys,keep_prob:0.7}) # 70%的神经元在工作 acc=sess.run(accuracy,feed_dict={x:mnist.test.images,y:mnist.test.labels,keep_prob:1.0}) print('Iter:'+str(epoch)+',Testing Sccuracy:'+str(acc))
运行结果:
Iter:0,Testing Sccuracy:0.8583 Iter:1,Testing Sccuracy:0.9681 Iter:2,Testing Sccuracy:0.9756 Iter:3,Testing Sccuracy:0.9803 Iter:4,Testing Sccuracy:0.9827 Iter:5,Testing Sccuracy:0.983 Iter:6,Testing Sccuracy:0.9861 Iter:7,Testing Sccuracy:0.9864 Iter:8,Testing Sccuracy:0.9876 Iter:9,Testing Sccuracy:0.9883 Iter:10,Testing Sccuracy:0.9884 Iter:11,Testing Sccuracy:0.9902 Iter:12,Testing Sccuracy:0.9905 Iter:13,Testing Sccuracy:0.9897 Iter:14,Testing Sccuracy:0.9905 Iter:15,Testing Sccuracy:0.9903 Iter:16,Testing Sccuracy:0.9905 Iter:17,Testing Sccuracy:0.9912 Iter:18,Testing Sccuracy:0.9912 Iter:19,Testing Sccuracy:0.9916 Iter:20,Testing Sccuracy:0.9902 从上面可以看出准确率可以达到99%