hdu 5730 Shell Necklace 分治FFT

Shell Necklace

题目连接：

http://acm.hdu.edu.cn/showproblem.php?pid=5730

Description

Perhaps the sea‘s definition of a shell is the pearl. However, in my view, a shell necklace with n beautiful shells contains the most sincere feeling for my best lover Arrietty, but even that is not enough.

Suppose the shell necklace is a sequence of shells (not a chain end to end). Considering i continuous shells in the shell necklace, I know that there exist different schemes to decorate the i shells together with one declaration of love.

I want to decorate all the shells with some declarations of love and decorate each shell just one time. As a problem, I want to know the total number of schemes.

Input

There are multiple test cases(no more than 20 cases and no more than 1 in extreme case), ended by 0.

For each test cases, the first line contains an integer n, meaning the number of shells in this shell necklace, where 1≤n≤105. Following line is a sequence with n non-negative integer a1,a2,…,an, and ai≤107 meaning the number of schemes to decorate i continuous shells together with a declaration of love.

Output

For each test case, print one line containing the total number of schemes module 313(Three hundred and thirteen implies the march 13th, a special and purposeful day).

Sample Input

3
1 3 7
4
2 2 2 2
0

Sample Output

14
54

Hint

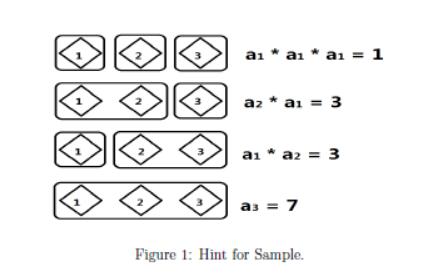
For the first test case in Sample Input, the Figure 1 provides all schemes about it. The total number of schemes is 1 + 3 + 3 + 7 = 14.

题意

题解：

推出显然的公式
(dp[i]= sum_{j=0}^{i-1}(dp[j]*a[i-j]))
也就是分治fft的经典形式

cdq(l,r)先算出前一半的真实dp值，后一半加上前一半的贡献，再递归后一半
每次操作为区间长度*log,总的复杂度nloglog

代码

//#include <bits/stdc++.h>
#include <stdio.h>
#include <iostream>
#include <string.h>
#include <math.h>
#include <stdlib.h>
#include <limits.h>
#include <algorithm>
#include <queue>
#include <vector>
#include <set>
#include <map>
#include <stack>
#include <bitset>
#include <string>
#include <time.h>
using namespace std;
long double esp=1e-11;
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#define fi first
#define se second
#define all(a) (a).begin(),(a).end()
#define cle(a) while(!a.empty())a.pop()
#define mem(p,c) memset(p,c,sizeof(p))
#define mp(A, B) make_pair(A, B)
#define pb push_back
#define lson l , m , rt << 1
#define rson m + 1 , r , rt << 1 | 1
typedef long long int LL;
const long double PI = acos((long double)-1);
const LL INF=0x3f3f3f3fll;
const int MOD = 313ll;
const int maxn=300000;
struct complex{
    double r,i;
    complex(double _r = 0.0,double _i = 0.0){r = _r; i = _i;}
    complex operator +(const complex &b){return complex(r+b.r,i+b.i);}
    complex operator -(const complex &b){return complex(r-b.r,i-b.i);}
    complex operator *(const complex &b){return complex(r*b.r-i*b.i,r*b.i+i*b.r);}
};
void change(complex y[],int len){
    int i,j,k;
    for(i = 1, j = len/2;i < len-1; i++){
        if(i < j)swap(y[i],y[j]);
        k = len/2;
        while( j >= k){
            j -= k;
            k /= 2;
        }
        if(j < k) j += k;
    }
}
void FFT(complex y[],int len,int on){  //len=2^k
    change(y,len);
    for(int h = 2; h <= len; h <<= 1){
        complex wn(cos(-on*2*PI/h),sin(-on*2*PI/h));
        for(int j = 0;j < len;j+=h){
            complex w(1,0);
            for(int k = j;k < j+h/2;k++){
                complex u = y[k];
                complex t = w*y[k+h/2];
                y[k] = u+t;
                y[k+h/2] = u-t;
                w = w*wn;
            }
        }
    }
    if(on == -1)
        for(int i = 0;i < len;i++)
            y[i].r /= len;
}
int callen(int len1,int len2){
    int len=1;
    while(len < len1*2 || len < len2*2)len<<=1;
    return len;
}
complex tf1[maxn],tf2[maxn];   //0~len1+len2-1,fftans[i] = y1[i] * y2[i]
int fftans[maxn];
void fft(int* y1,int len1,int* y2,int len2){ //0~len1-1,0~len2-1
    int len=callen(len1,len2);
    for(int i = 0;i < len1;i++)
        tf1[i] = complex(y1[i],0);
    for(int i = len1;i < len;i++)
        tf1[i] = complex(0,0);
    for(int i = 0;i < len2;i++)
        tf2[i] = complex(y2[i],0);
    for(int i = len2;i < len;i++)
        tf2[i] = complex(0,0);
    FFT(tf1,len,1);
    FFT(tf2,len,1);
    for(int i = 0;i < len;i++)
        tf1[i] = tf1[i]*tf2[i];
    FFT(tf1,len,-1);
    for(int i = 0;i < len1+len2-1;i++)
        fftans[i] = tf1[i].r+0.5;
}
int A[maxn],Ans[maxn];
void solve(int l,int r){
    int m=(l+r)>>1;
    fft(Ans+l,m-l+1,A,r-l+1);
    for(int i = m-l+1;i <=r-l;i++)
        Ans[i+l]=(Ans[i+l]+fftans[i])%MOD;
}
void CDQ(int L,int R){
    if(L==R)return;
    int m=(L+R)>>1;
    CDQ(L,m);
    solve(L,R);
    CDQ(m+1,R);
}
int main()
{
    //freopen("in.txt", "r", stdin);
    //freopen("inlay.in", "r", stdin);
    //freopen("out.txt", "w", stdout);      %I64d
    //vector<int>::iterator iter;
    //memset(m,0,sizeof(int));
    //for(int x=1;x<=n;x++)
    //for(int y=1;y<=n;y++)
    //scanf("%d",&a);
    //printf("%d
",ans);
    while(1)
    {
        int n;
        scanf("%d",&n);
        if(n==0)break;
        memset(Ans,0,(callen(n,n)+10)*sizeof(int));
        Ans[0]=1;
        memset(A,0,(callen(n,n)+10)*sizeof(int));
        for(int x=1;x<=n;x++)
        {
            scanf("%d",&A[x]);
            A[x]%=MOD;
        }
        CDQ(0,n);
        printf("%d
",(Ans[n]+MOD)%MOD);
    }
    return 0;
}