机器学习4logistic回归

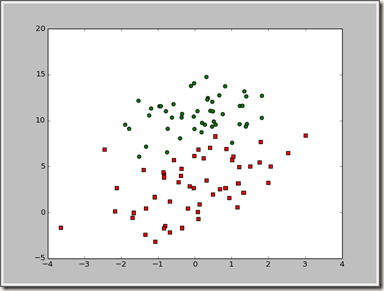
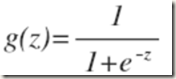对于线性回归、logistic回归，在以前准备学习深度学习的时候看过一点，当时的数学基础有点薄弱，虽然现在还是有点差，当时看到神经网络之后就看不下去了。

不过这次是通过python对logistic回归进行编码实现。

线性回归跟逻辑回归介绍就不多说了。网上有很多很好的讲解。另外我之前也写过自己学习斯坦福Andrew.Ng的课程的笔记，如下：

http://www.cnblogs.com/fengbing/archive/2013/05/15/3079033.html

http://www.cnblogs.com/fengbing/archive/2013/05/15/3079399.html

http://www.cnblogs.com/fengbing/archive/2013/05/15/3080679.html

http://www.cnblogs.com/fengbing/archive/2013/05/18/3086284.html

http://www.cnblogs.com/fengbing/archive/2013/05/18/3086324.html

http://www.cnblogs.com/fengbing/archive/2013/05/19/3086403.html

以及logistic回归的推广softmax回归http://www.cnblogs.com/fengbing/archive/2013/05/20/3088466.html

说的简单一点，逻辑回归就是线性回归做了一个逻辑映射

这个映射函数一般为

公式推导参考http://www.cnblogs.com/fengbing/p/3518684.html

具体python代码

from numpy import *

def loadDataSet():
    dataMat = []; labelMat = []
    fr = open('testSet.txt')
    for line in fr.readlines():
        lineArr = line.strip().split()
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
        labelMat.append(int(lineArr[2]))
    return dataMat,labelMat

def sigmoid(inX):
    return 1.0/(1+exp(-inX))

#参考http://www.cnblogs.com/fengbing/p/3518684.html
def gradAscent(dataMatIn, classLabels):
    dataMatrix = mat(dataMatIn)
    labelMat = mat(classLabels).transpose() 
    m,n = shape(dataMatrix)#返回矩阵行跟列数100，3
    alpha = 0.001
    maxCycles = 500#最高的迭代次数
    weights = ones((n,1))#[1,1,1]T这个权重可能随便给一个初始值
    for k in range(maxCycles):              
        h = sigmoid(dataMatrix*weights)     
        error = (labelMat - h)
        weights = weights + alpha * dataMatrix.transpose()* error 
    return weights

结果如下：

>>> import logRegres
>>> dataArr,labelMat = logRegres.loadDataSet()
>>> logRegres.gradAscent(dataArr,labelMat)
matrix([[ 4.12414349],
        [ 0.48007329],
        [-0.6168482 ]])

这样可以直接计算最后权重的值，不过如何更好的理解了，图形化，下面分析数据画出决策边界

代码如下：

  1: def plotBestFit(weights):

  2:     import matplotlib.pyplot as plt

  3:     dataMat,labelMat=loadDataSet()

  4:     dataArr = array(dataMat)

  5:     n = shape(dataArr)[0]#数组长度100

  6:     xcord1 = []; ycord1 = []

  7:     xcord2 = []; ycord2 = []

  8:     for i in range(n):

  9:         if int(labelMat[i])== 1:

 10:             xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])

 11:         else:

 12:             xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])

 13:     fig = plt.figure()

 14:     ax = fig.add_subplot(111)

 15:     ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')

 16:     ax.scatter(xcord2, ycord2, s=30, c='green')

 17:     x = arange(-3.0, 3.0, 0.1)

 18:     y = (-weights[0]-weights[1]*x)/weights[2]

 19:     ax.plot(x, y)

 20:     plt.xlabel('X1'); plt.ylabel('X2');

 21:     plt.show()

首先我们得到了最后分类函数 y=θ0+θ1x1+θ2x2

我们画出y=0这条直线 x1在-3到3直接相差为1的值

则x2=（-θ0-θ1x1）/θ2

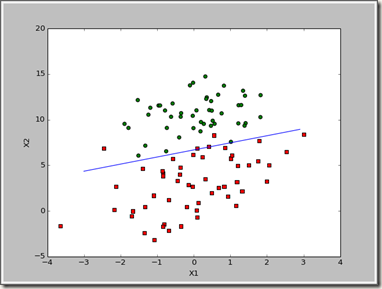
最后得出的结果如下：

>>> import logRegres

>>> dataArr,labelMat = logRegres.loadDataSet()

>>> weights = logRegres.gradAscent(dataArr,labelMat)

>>> logRegres.plotBestFit(weights.getA())

这个梯度上升算法在每次更新回归系数的时候都要遍历整个数据集，目前是处理100个左右的数据，如果有数十亿样本，那这个算法的复杂度就非常好了，一种改进的办法是一次仅用一个样本来更新回归系数，这个方法叫随机梯度上升算法。

由于可以在新的样本到来时对分类器进行增量式更新，因此这个随机梯度上升算法也是一个在线学习算法。

伪代码如下：

def stocGradAscent0(dataMatrix, classLabels):

    m,n = shape(dataMatrix)#得到数据集矩阵大小100，3

    alpha = 0.01

    weights = ones(n)

    print weights

    for i in range(m):

        h = sigmoid(sum(dataMatrix[i]*weights))

        print h

        error = classLabels[i] - h

        weights = weights + alpha * error * dataMatrix[i]

    return weights

最终结果：

>>> import logRegres
>>> dataArr,labelMat = logRegres.loadDataSet()
>>> weights = logRegres.stocGradAscent0(array(dataArr),labelMat)
>>> logRegres.plotBestFit(weights)

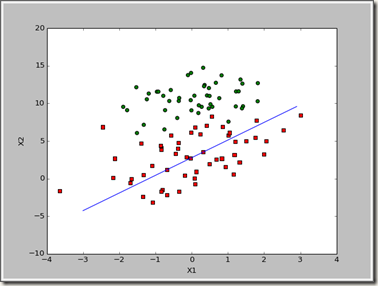
虽然这个拟合的结果没有刚刚好的，不过这个迭代的次数少，不过对于我们数据挖掘来说要优先考虑准确性，再考虑效率，于是要对该算法进行优化。

下面进行改进，添加alpha值的改变，已经用于计算的样本随机选取。

def stocGradAscent1(dataMatrix, classLabels, numIter=150):
    m,n = shape(dataMatrix)
    weights = ones(n)   
    for j in range(numIter):
        dataIndex = range(m)
        for i in range(m):
            alpha = 4/(1.0+j+i)+0.0001
            randIndex = int(random.uniform(0,len(dataIndex)))
            h = sigmoid(sum(dataMatrix[randIndex]*weights))
            error = classLabels[randIndex] - h
            weights = weights + alpha * error * dataMatrix[randIndex]
            del(dataIndex[randIndex])
    return weights

结果：

>>> import logRegres
>>> dataArr,labelMat = logRegres.loadDataSet()
>>> weights = logRegres.stocGradAscent1(array(dataArr),labelMat)
>>> logRegres.plotBestFit(weights)

最后给出一个真正预测的问题，解决病马的生死预测问题。

具体流程：

这边解决一个问题，数据预处理部分的缺失值处理。

一般我们有如下处理方法：

1、忽略元组，就是这个数据的类别不知道的时候，还有就是这个样本的很多属性都缺失

2、人工填写，该方法比较费时

3、使用一个全局常量填充缺失值如-1，这个方法不太可靠

4、使用属性的均值来替代

5、使用与给定样本属于同一类的所有样本的属性均值

6、使用最有可能的值填充缺失值,通过贝叶斯、回归等方法给出缺失值

在这个例子中，我们处理如下方法

1、所有的缺失值用一个必须用一个实数值来代替，这个是NumPy不允许包含缺失值。这边用0来代替，比较适合Logistic回归。

这样如果缺失值是0的话，这样这个特征不影响系数值。另外sigmoid（0） = 0.5 这对结果预测也不具备任何倾向性。

2、如果在测试集中发现了一条数据的类别标签已经缺失，这边做法简单，将其丢弃掉。

好，下面就是算法的使用，我们通过训练集先计算得到参数，这样我们就可以得到方程式如y=θ0+θ1x1+θ2x2再将求得的y带入到sigmoid函数中看其与0.5的比较，大就是1，不是就是0.

主要就是对这个数据中多少属性，以及数据量清楚，存入数组中处理。

最后评估了这个模型，计算了10词错误率的平均值。

def classifyVector(inX, weights):
    prob = sigmoid(sum(inX*weights))
    if prob > 0.5: return 1.0
    else: return 0.0

def colicTest():
    frTrain = open('horseColicTraining.txt'); frTest = open('horseColicTest.txt')
    trainingSet = []; trainingLabels = []
    for line in frTrain.readlines():
        currLine = line.strip().split('	')
        lineArr =[]
        for i in range(21):
            lineArr.append(float(currLine[i]))
        trainingSet.append(lineArr)
        trainingLabels.append(float(currLine[21]))
    trainWeights = stocGradAscent1(array(trainingSet), trainingLabels, 1000)
    errorCount = 0; numTestVec = 0.0
    for line in frTest.readlines():
        numTestVec += 1.0
        currLine = line.strip().split('	')
        lineArr =[]
        for i in range(21):
            lineArr.append(float(currLine[i]))
        if int(classifyVector(array(lineArr), trainWeights))!= int(currLine[21]):
            errorCount += 1
    errorRate = (float(errorCount)/numTestVec)
    print "the error rate of this test is: %f" % errorRate
    return errorRate

def multiTest():
    numTests = 10; errorSum=0.0
    for k in range(numTests):
        errorSum += colicTest()
    print "after %d iterations the average error rate is: %f" % (numTests, errorSum/float(numTests))

结果：

>>> import logRegres
>>> logRegres.multiTest()

Warning (from warnings module):
  File "E:Machine Learningexercisech05logRegres.py", line 13
    return 1.0/(1+exp(-inX))
RuntimeWarning: overflow encountered in exp
the error rate of this test is: 0.328358
the error rate of this test is: 0.343284
the error rate of this test is: 0.432836
the error rate of this test is: 0.402985
the error rate of this test is: 0.343284
the error rate of this test is: 0.343284
the error rate of this test is: 0.283582
the error rate of this test is: 0.313433
the error rate of this test is: 0.432836
the error rate of this test is: 0.283582
after 10 iterations the average error rate is: 0.350746

这边有一个警告，是可能溢出的警告，查了一下，可以使用

http://pythonhosted.org/bigfloat/#module-bigfloat

或者直接忽略警告。这边我没有处理，有好的处理方法，大家分享。

这个逻辑回归就到这边，主要采用了梯度下降算法，另外Andrew.Ng也讲了牛顿法，这本书结束会对没有写到的一些算法做一些考虑。