原题地址:
https://leetcode.com/problems/partition-equal-subset-sum/description/
题目:
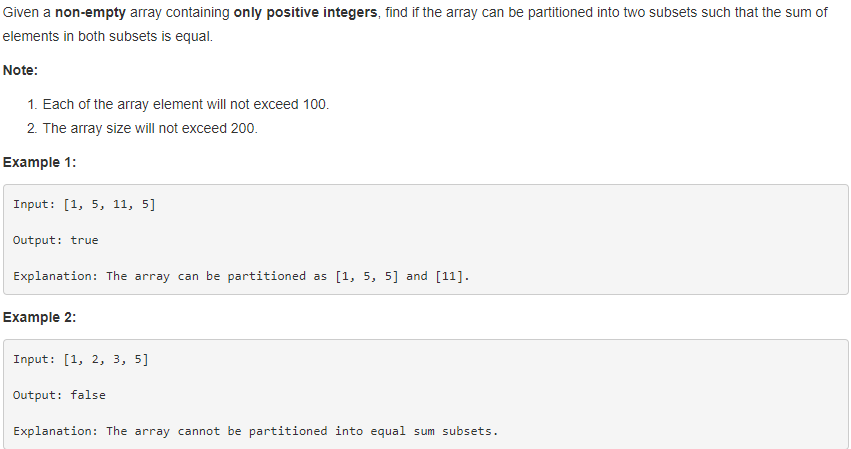
题解:
这道题给定一个数组,求这个数组是否可以分成两个数组,使这两个数组各自的元素之和相等。
首先,假如这个数组本身的元素之和是一个奇数时,是不能把这个数组分成两个和相等的数组的。因此,利用这一点我们可以排除掉很多情况,直接得出结果。
而对于数组本身元素之和为偶数的情况,我们才需要算法去解决。我们可以将问题转化为以下的形式:是否有一个子数组的元素之和,恰好等于原数组元素之和的一半呢?而对于原数组中的每一个元素,都有两种状态:在子数组里面或者不在子数组里面(先假设存在这个子数组)。这样一看,我们就能发现这个问题与0-1背包问题非常相似,因此我们可以采用0-1背包问题的解法去解决这道问题。
在这道题目中,原数组里面的每个元素都可以看作是一种物品,而这件物品的重量和价值都为元素值;原数组的和的一半可看作背包的最大承重量,而当背包能放下物品的最大价值为原数组和的一半时,就返回真,否则返回假。
采用二维数组解决的代码如下:
class Solution { public: bool canPartition(vector<int>& nums) { int sum = accumulate(nums.begin(), nums.end(), 0); if (sum % 2 == 1) return false; sum /= 2; int ** a = new int*[nums.size()]; for (int i = 0; i < nums.size(); i++) { a[i] = new int[sum + 1]; } for(int i=nums[0];i<=sum;i++){ a[0][i] = nums[0]; } for (int i = 1; i < nums.size(); i++) { for (int j = nums[i]; j <= sum; j++) { a[i][j] = a[i - 1][j] > a[i - 1][j - nums[i]] + nums[i] ? a[i - 1][j] : a[i - 1][j - nums[i]] + nums[i]; } } return a[nums.size() - 1][sum] == sum; } };
上面的代码值得注意的是下面这一句:
for(int i = nums[0]; i <= sum;i++){ a[0][i] = nums[0]; }
由于这道题目中“物品”是从第0件开始算起的,这和平时做的0-1背包问题从第1件物品算起的初始化方法不一样,值得注意。
采取一维数组解决的代码:
class Solution { public: bool canPartition(vector<int>& nums) { int sum = accumulate(nums.begin(), nums.end(), 0); if (sum % 2 == 1) return false; sum /= 2; int * dp = new int[sum + 1];for (int i = 0; i < sum + 1; i++) {
dp[i] = 0;
}for (int i = 0; i < nums.size(); i++) { for (int j = sum; j >= nums[i]; j--) { dp[j] = dp[j] > dp[j - nums[i]] + nums[i] ? dp[j] : dp[j - nums[i]] + nums[i]; } } return dp[sum] == sum; } };
用一维数组来解决这个问题,就无需考虑上面从第几件物品算起的问题,只需改一下第一层循环i的起始值即可。
这道题给了我一个启发:这类题目,即物品(数组元素)有存在与否两种状态的题目,都可以用0-1背包的思想和解法进行解决。推广一下,可以用背包问题的思想去解决。(假如允许数组元素重复岂不是可以用完全背包的方法解决?)