题面:
Description
Nick最近在玩一款很好玩的游戏,游戏规则是这样的:
有一个n*m的地图,地图上的每一个位置要么是空地,要么是炮塔,要么是一些BETA狗,Nick需
要操纵炮塔攻击BETA狗们。
攻击方法是:对于每个炮塔,游戏系统已经给出它可以瞄准的方向(上下左右其中一个),Nick需要
选择它的攻击位置,每一个炮塔只能够攻击一个位置,炮塔只能够向着它的瞄准方向上的某个位置发
动攻击,当然炮塔也可以不进行攻击。炮塔威力强大,它可以且仅可以消灭目标位置上所有的BETA狗。
出于安全考虑,游戏系统已经保证不存在一个炮塔能够瞄准另外一个炮塔,即对于任意一个炮
塔,它所有可能的攻击位置上不存在另外一个炮塔。而且,如果把炮塔的起点和终点称为炮弹的运行
轨迹,那么系统不允许两条轨迹相交(包括起点和终点)。
现在,选定目标位置以后,每一个炮塔同时开炮,你要告诉Nick,他最多可以干掉多少BETA狗。
Input
第一行两个正整数n,m,表示地图的规模。
接下来礼行,每行m个整数,0表示空地,-1,-2,一3,-4分别表示瞄准上下左右的炮塔,若为正整
数p,则表示该位置有p个BETA狗。
n,m <= 50,每个位置的BETA狗数量不超过999个,保证不存在任意一个炮塔能够瞄准另外一个炮塔
Output
一个正整数,表示Nick最多可以干掉几个BETA狗
Sample Input
3 2
0 9
-4 3
0 -1
Sample Output
9
分析:
显然,题目保证了只有横炮台与纵炮台才可能会有相交的攻击轨迹。
然后对于每对有相交攻击范围的横炮台与纵炮台,它们对答案的贡献得分不仅决定于它们自己的攻击范围内的BETA狗,还会被其它的炮台所局限。所以,每个炮台对于进攻目标的选择,正好需要最大流最小割的类似自我调整的性质。
考虑如何连边。如果从最大流的角度思考,难以表达“炮台A选了BEAT狗a,炮台B就不能选a”这种逻辑关系,所以改换最小割。若一对纵横炮台A与B存在公共轨道,可以看成A到B有一条路径,就像这样:
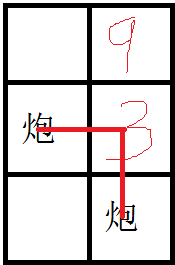
那么我们割就是让两个炮台无法相交。
如果两个炮台要攻击最大值时都要去跨过它们攻击轨道的相交点,那么我们的割就要让其中一个炮台无法越过相交点,另一个不再受那个炮台的约束。
我们可以把所有点拿出来当一个部,每个炮台的轨道上的点依次连边。
若该轨道为纵向,则轨道上的第一个点与原点连边,方向与炮台方向相同,同理连第一个点与第二个点,方向与炮台相同(因为打到一个点时,它之前的点会被轨道覆盖,所以不能分别与原点连边),以此类推。若该轨道为横向,则第一个点与汇点连边,方向与炮台方向相反,以此类推。
又因为两个炮台之间的路径只能有一次拐弯,故拆点,左边的点表示纵向轨迹,右边的点表示横向轨迹,相同的点之间从左到右连一条边。
这样就可以表示出全部的纵炮到横炮的路径(纵横可以反过来)。
接下来考虑一下割边的代价。
我们先来考虑割边的意义。割某条边就代表有一个炮台打到的点只能是那个边的一个端点,而另外一个的炮台就不再受这个炮台的限制。
所以,首先满足的是割的边必须是同一条轨道上相邻点之间的边,所以 相同点之间的边 和 点与汇点,源点的边 的代价(即容量)为inf。这样它们就不会被割了。
对于其它边的讨论,容我摘一段xmy大佬的解释:
把炮塔能够打到的beta狗中的最大值记为mx,那么炮塔路径最多只会延伸到第一个mx,再往后只会更劣。我们先把每个炮塔的mx加入ans中。
对于竖炮塔的一条边u->v,割掉它表示炮塔打到了u点,那么ans就会损失掉mx-u点的beta狗的值,于是这条边的容量为mx-u点的beta狗。
对于横炮塔的一条边u->v,割掉它表示炮塔打到了v点,那么ans就会损失掉mx-v点的beta狗的值,于是这条边的容量为mx-v点的beta狗。
所以答案就是ans-最小割。
最后附上代码
#include<cstdio>
#include<cstring>
#include<algorithm>
#define p(i,j) (i-1)*m+j
using namespace std;
const int maxp=5005,inf=0x3f3f3f3f;
int n,m,tot,map[55][55], dx[4]={-1,1,0,0},dy[4]={0,0,-1,1},d[maxp],vd[maxp];
int S,T,ans,cnt=1,sum,info[maxp];
struct flow{int u,v,nex,w;}e[30005];
int sap(int i,int augco)
{
if(i==T)return augco;
int j,tmp,ret=0,mind=T-1;
for(int o=info[i];o;o=e[o].nex)
{
j=e[o].v;
if(e[o].w>0){
if(d[i]==d[j]+1)
{
tmp=sap(j,min(e[o].w,augco));
e[o].w-=tmp;
e[o^1].w+=tmp;
ret+=tmp;
augco-=tmp;
if(d[1]>=T)return ret;
if(augco==0)break;
}
mind=min(mind,d[j]);
}
}
if(ret==0)
{
vd[d[i]]--;
if(vd[d[i]]==0)
d[1]=T;
d[i]=mind+1;
vd[d[i]]++;
}
return ret;
}
void solve()
{
memset(vd,0,sizeof vd);
memset(d,0,sizeof d);
vd[0]=T;ans=0;
while(d[S]<T)
ans+=sap(1,inf);
}
void add(int u,int v,int w)
{
//printf("%d %d %d
",u,v,w);
e[++cnt]=(flow){u,v,info[u],w};info[u]=cnt;
e[++cnt]=(flow){v,u,info[v],0};info[v]=cnt;
}
int main()
{
scanf("%d%d",&n,&m);S=1;T=1+n*m+n*m+1;
for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)scanf("%d",&map[i][j]);
for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)if(map[i][j]<0)
{
int k=-map[i][j]-1,mx=0,x,y;
map[i][j]=0;
for(x=i+dx[k],y=j+dy[k];1<=x&&x<=n&&1<=y&&y<=m;x+=dx[k],y+=dy[k])mx=max(mx,map[x][y]);
sum+=mx;
if(k==0||k==1)
{
add(S,1+p(i,j),inf);
for(x=i,y=j;map[x][y]!=mx;x+=dx[k],y+=dy[k])
add(1+p(x,y),1+p(x+dx[k],y+dy[k]),mx-map[x][y]);
}
if(k==2||k==3)
{
add(1+n*m+p(i,j),T,inf);
for(x=i,y=j;map[x][y]!=mx;x+=dx[k],y+=dy[k])
add(1+n*m+p(x+dx[k],y+dy[k]),1+n*m+p(x,y),mx-map[x][y]);
}
}
for(int i=1;i<=n*m;i++) add(1+i,1+n*m+i,inf);solve();
printf("%d
",sum-ans);
}