Q: 数组的创建?
A: Java中有两种数据类型,基本类型和对象类型,在许多编程语言中(甚至面向对象语言C++),数组也是基本类型。但在Java中把数组当做对象来看。因此在创建数组时,必须使用new操作符:
int [] objArray = null; // defines a reference to an array
objArray = new int[100]; // creates the array, and sets objArray to refer to it
或使用等价的单语句声明和定义:
int[] objArray = new int[100];
[]操作符对于编译器来说是一个标志,它说明正在命名的是数组对象而不是普通的变量。 由于数组是一个对象,所以它的名字(如本例中的objArray)是数组的一个引用,它不是数组本身。数组存储在堆空间的某一个地址中,而objArray仅仅保存着这个地址。
数组有一个length属性,通过它可以得知当前数组的大小。
正如大多数编程语言一样,一旦创建数组,数组大小不可改变。
Q: 数组的初始化列表?
A: 创建一个对象数组如下:
AutoData[] cars = new AutoData[400];
除非将特定的值赋给数组的数据项,否则它们一直是特殊的null对象。如果尝试访问一个含有null的数组数据项,程序会出现Null Pointer Assignment的运行时错误,这主要是为了保证在读取某个数据项之前要先对其赋值。
使用下面的语法可以对一个基本类型的数组初始化:
int[] nArray = {0, 3, 6, 9, 12, 15, 18, 21, 24, 27};
上面的语句可能简单得令人惊讶,它同时取代了引用声明和使用new来创建数组。在大括号中的数据被称为初始化列表。数组大小由列表数据项的个数决定。
Q: 面向过程编程的数组示例?
A: 先介绍一个老式的面向过程编程(POP)的版本,然后再介绍一个可以达到同样效果的面向对象编程(OOP)的版本。
关于POP和OOP的思想,可以参考博客《编程思想的理解(POP,OOP,SOA,AOP)》
A: 通常数据结构中存储的数据项包含有好几个字段,所以应该由对象而不是简单类型来代表它们。在本示例中,为了简化所以数组中存储的数据类型为long型。
A: 在查找过程中,用searchKey一个一个地与数组中的数据项比较,如果循环变量i变化到最后一个数据项,但是仍旧没有匹配上,这个值就不在数组中。
A: 在删除过程中,找到删除的数据项后,向前移动所有下标比它大的数据项来填补删除后留下来的“坑”,并将size减一。
Q: 面向对象编程的数组示例(一)?
A: 上面示例是一个老式的面向过程的程序,那么怎么把它改成面向对象编程的程序呢?首先要将数据存储(数组)从程序分离出来,程序的其他部分成为使用这个结构的用户;其次是改进存储结构和用户之间的通信。
A: 现在把这个数组封装在一个类中,叫做LowArray。可以将LowArray类想成是工具,LowAppTest类时工具的使用者,现在程序被划分成两个不同角色的类,这对于编写一个面向对象的程序来说是关键的第一步。
示例:LowArray.java, LowArrayTest.java
A: 用来存储数据对象的类有时被称作容器类(container class),例如LowArray类,通常容器类不仅存储数据,并且提供访问数据的方法和其他诸如排序等复杂的操作。
Q: 面向对象编程的数组示例(二)?
A: 上面的示例只是演示了如何将一个程序划分为类,但它并没有带给我们太多的实际价值,下面要做的是重新分配类之间的责任,从而可以获得更多的OOP的好处。
A: 上面的示例中数据存储结构的使用者必须知道数组的下标,setElement()和getElement()方法还是在低层次构思了,它们与普通Java数组中[]操作符没什么区别。但有些用户只需要随机访问数组数据项,不太需要知道数组的下标,因此他不会意识到数组下标是有用或有关系的。
示例:HighArray.java, HighArrayTest.java
A: HighArray程序给出了数据结构的一个改进接口,类用户(HighArrayTest)使用接口就不再考虑下标了,它取消了setElement()和getElement()方法,取而代之是insert(), find()和delete()。因为由类来负责处理下标问题,所以这些方法不再需要将下标当做参数。类用户可以集中精力于在做什么而不是怎么做:什么要被插入、删除和访问,而不是如何执行这些操作。
A: 请留意main()是多么地短小简单。在LowArray中必须由main()处理的细节现在被HighArray类中的方法解决了。比如insert()方法向数组下一个空位置上放置一个新的数据项,一个名为mSize的字段跟踪记录着数组中实际已有的数据项个数。main()方法不再需要为数组中还有多少数据项而担心了。
A: 令人惊讶的是,类用户甚至不必知道HighArray类中使用何种数据结构存储数据,结构被隐藏在接口之后。
Q: 有序数组的Java示例 ?
A: 假设一个数组内的数据项都按关键字进行排序,这种数组被称为有序数组?为什么要进行排序呢?好处之一是可以通过二分查找显著地提高查找速度。
A: 下面讨论一下有序数组的Java代码,OrderArray类的核心是find()方法,通过它可以二分查找来定位一个特定的数据项。
示例: AscOrderArray.java, OrderedArrayTest.java
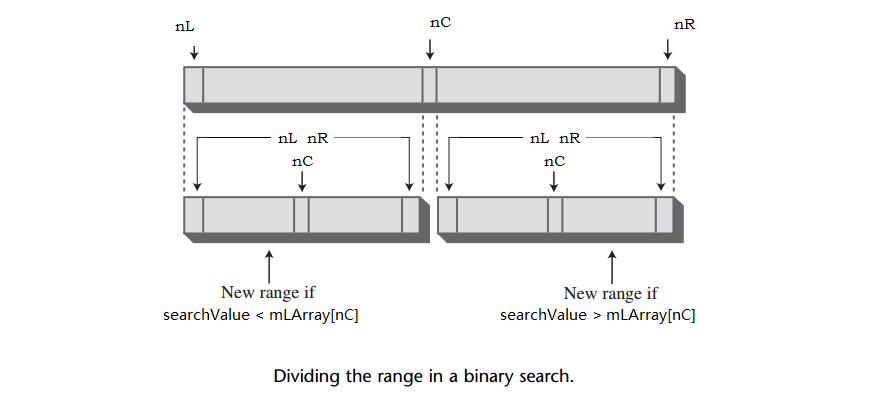
find()方法通过将数组数据项范围不断对半分割来查找特定的数据项,这个方法在一开始设变量nL和nR指向数组的最左边和最右边非空的数据项。然后在while循环中,当前的下标nC被设置为这个范围的中间值。
如果幸运的话,nC可能直接就指向所需的数据项,所以应先查看是否相等,如果是,则意味着找到该数据项,下一步就是返回它的下标nC。
循环中的每一步将范围缩小一半,最终这个范围会小到无法分割(当nL等于nR,范围是一个数据项,所以还需要再一次循环),当范围不再有效时停止查找,但没有找到所需的数据项,所以返回下标-1,表示失败。
Q: 有序数组的优缺点 ?
A: 优点:查找的速度比无序数组快多了。
缺点:插入操作中由于所有靠后的数据项都需要移动以腾开空间,所以速度慢。
有序数组和无序数组中的删除操作都很慢,这是因为数据项必须向前移动来填补已删除数据项的“坑”。
Q: 存储对象的数组示例?
A: 上面的Java示例中,数据结构中只存储long类型的简单变量,存储这些变量简化了程序,但它对如何在现实世界中使用数据存储结构来说没有代表性,通常我们存储的数据记录是许多字段的结合。例如一条职员记录需要存储姓、名、年龄、社会保险号等等。
下面的Java示例中给出对象是如何存储的,而不再是简单类型的变量了。这里使用泛型技术,能够更高复用代码。
示例: ObjectArray.java, Person.java, ObjectArrayTest.java
Q: 大O表示法?
A: 在比较算法时似乎应该说一些类似“算法A比算法B快两倍”之类的话,但实际上这类陈述并没有多大的意义。为什么呢?这是由于当数据项个数变化时,对应的比例也会发生根本改变。有可能数据项增加了50%,则A比B快了3倍;或有可能只有一半的数据项,但现在A和B的速度是相同的。
A: 我们需要的是一个可以描述算法的速度是如何与数据项的个数相关联的比较,这就用到大O表示法。
Q: 无序数组的插入时间?
A: 无论数组中的数据项个数N有多大,一次插入总是用相同的时间,新数据项总是被放在下一个有空的地方,即array[size++]。我们可以说向一个无序数组中插入一个数据项的时间T是一个常数K:
T = K
A: 在现实情况中,插入所需的实际时间(不管是纳秒、微妙好还是其他单位)与以下因素有关:微处理器,编译后可执行文件的执行效率等等。上面等式中的常数K包含了所有这些因素,在现实情况中要得到K的值,需要测量一次插入所花费的时间。K就等于这个时间。
Q: 数组线性查找的时间?
A: 在数组数据项的线性查找中,寻找特定数据项所需的比较次数平均为数据项总数的一半。即T = K * (N / 2)。K是上面所说的常数,将2并入K可以得到一个更方便的公式。新K'值等于原先K除以2。新公式为:
T = K' * N
这个方程说明平均线性查找时间与数组的大小成正比。
Q: 数组二分查找时间?
A: 二分查找的公式如下:
T = K * log2(N)
时间T与以2为底N的对数成正比。
为什么是以2为底的对数呢?
我们小时候经常玩猜数字游戏,假设这个数字的范围是1 - 100。我们习惯性地先从100的一半开始,然后不断地再以一半的范围去猜测。这个过程就是不断地除以2,直到找到我们猜对的数字。反过来逆推这个过程,就是不断乘以2,即多少次2的自乘,2x = 100。自然这个猜测次数x就是以2为底100的对数。
从底数为2转换为底数为10需乘以3.322,我们可以将这个3.322常数也并入K',由此不必指定底数:
T = K' * lg(N)
关于这个3.322怎么来的,请看下面的公式: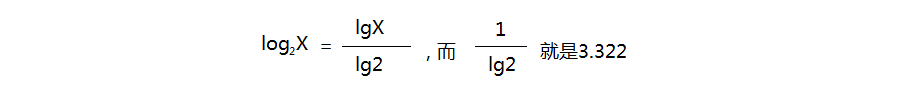
Q: 什么是幂?
A: 幂,指乘方运算的结果。nm指将n自乘m次, 把nm看作乘方的结果,叫做“n的m次幂”。
其中,n称为“底数”,m称为“指数”。
A: 掌握以下运算规则:
1) 同底数幂相乘,底数不变,指数相加;
2) 同底数幂相除,底数不变,指数相减;
3) 幂的乘方,底数不变,指数相乘
A: 零指数幂 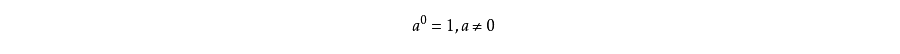
A: 负指数幂 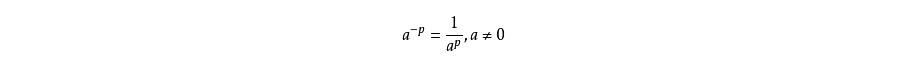
A: 分数指数幂
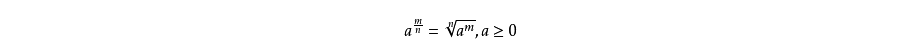
Q: 什么是指数函数?
A: 指数函数(exponential function),一般地,y=ax函数(a为常数且以a>0,a≠1)叫做指数函数,函数的定义域是R。
A: 基本性质:
1) 指数函数的定义域为R,这里的前提是a大于0且不等于1。对于a不大于0的情况,则必然使得函数的定义域不连续,因此我们不予考虑,同时a等于0函数无意义一般也不考虑;
2) 指数函数的值域为(0,+∞);
3) a > 1时,则指数函数单调递增;若0 < a < 1,则为单调递减的;
4) 函数总是通过(0,1)这点;
5) 指数函数具有反函数,其反函数是对数函数;
A: 运算法则: 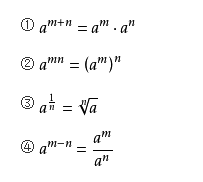
Q: 什么是对数函数?
A: 如果ax=N(a > 0,且a≠1),那么数x叫做以a为底N的对数,记作x=logaN,读作以a为底N的对数。“log”是拉丁文logarithm(对数)的缩写。
A: 一般地,函数y=logax(a>0,且a≠1)叫做对数函数,也就是说以幂为自变量,指数为因变量,底数为常量的函数,叫对数函数。
A: 通常我们将以10为底的对数叫常用对数(common logarithm),并把log10N记为lgN。
A: 在科学计数中常使用以无理数e=2.71828···为底数的对数,以e为底的对数称为自然对数(natural logarithm),并且把logeN 记为InN。
A: 基本性质:
1) 定义域是{x 丨x > 0}, 值域为实数集R;
2) 对数函数的函数图像恒过定点(1,0);
3) a>1时,在定义域上为单调增函数, 0 < a < 1时,在定义域上为单调减函数;
A: 运算法则: 
Q: 几个常用算法的大O比较?
A: 当比较算法时,并不在乎具体的微处理器芯片或编译器,真正需要比较的是对应不同的N值,因此不需要常数。
A: 大O表示法使用大写字母O,可以认为其含义是"order of"大约是的意思。
下标是总结我们目前为止讨论过的算法的运行时间。 
A: 通过它我们可以比较不同的大O值:O(1)是优秀,O(logN)是良好,O(N)是还可以,O(N2)则差一些。
大O表示法的实质并不是对运行时间给出实际值,而是表达了运行时间是如何受数据项个数所影响的。 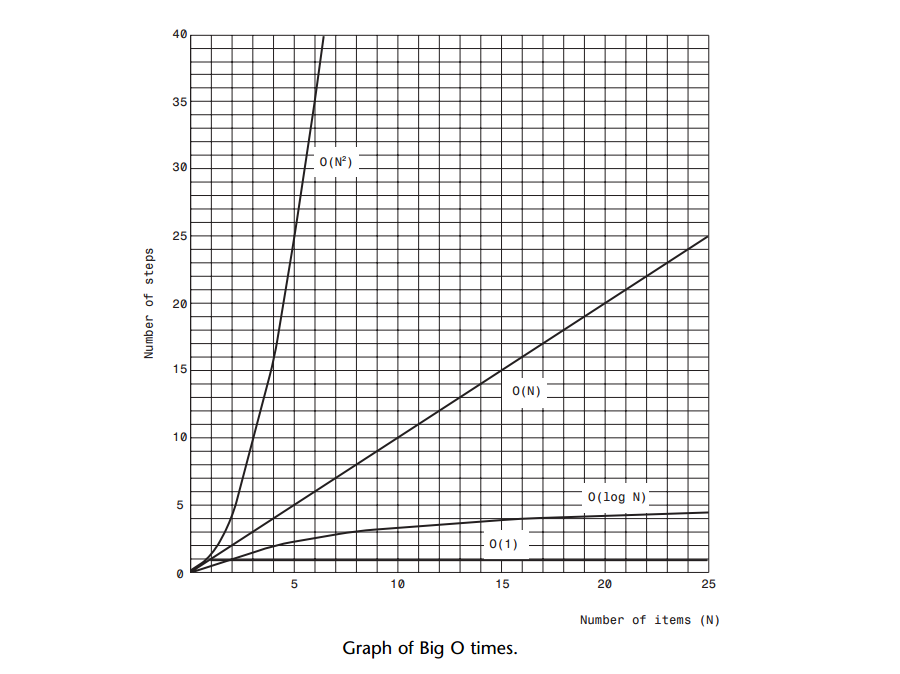
Q: 为什么不用数组表示一切?
A: 仅用数组似乎就可以完成所有工作,那为什么不用它们来进行所有数据的存储呢?
我们已经看到了许多关于数组的缺点。如在一个无序数组的插入时间很快,但是查找却要花费较慢的时间。在一个有序数组中可以查找得很快,但插入却花费很长的时间。对于这两种数组而言,删除操作时间也很慢。
如果有一种数据结构进行任何操作如插入、删除和查找都很快(理想是O(1)或者是O(logN))的时间,那就好了。
数组的另一个问题便是它们被new创建后,大小尺寸就被固定了。但通常在开始设计程序时并不知道会有多少数据项会被放入数组中,所以需要猜它的大小。如果猜的数过大,会使数组中的某些元素永远不会被填充而浪费空间。如果猜小了,会发生数组溢出。
A: Java中有一个被称为Vector类,使用起来很像数组,但是它可以扩展,这些附加的功能是以效率作为代价的。
你可能想尝试创建自己的向量(vector)类。当类用户使用类中内部数组将要溢出时,插入算法创建一个大一点的数组,把旧数组中的内容复制到新数组中,然后再插入新数据项。整个过程对于类用户来说是不可见的。