LeetCode 动态规划专题
53. 最大子序和

集合+属性:所有以i结尾的子数组 的最大值
状态计算: 1.最后一个不同点 2.子集划分
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int n = nums.size();
vector<int> f(n+1);
if(n == 0) return 0;
f[0] = max(0,nums[0]);
int ans = nums[0];
bool flag = false;
for(int i=0;i<n;i++)
if(nums[i] >= 0) flag = true;
int maxAns = nums[0];
for(int i=1;i<n;i++){
maxAns = max(nums[i],maxAns);
f[i] = max(f[i-1]+nums[i],0);
ans = max(ans,f[i]);
}
if(!flag) return maxAns;
return ans;
}
};
代码逻辑优化:滚动数组(这里一个变量),因为只用到了f[i-1]
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int ans = INT_MIN,last = 0;
for(int i=0;i<nums.size();i++){
int now = max(last,0) + nums[i];
ans = max(ans,now);
last = now;
}
return ans;
}
};
120. 三角形最小路径和
集合+属性:f(i,j) 所有坐标以i,j为终点的路径的集合 中的路径和最小值
状态计算:f(i,j) = 以正下方或斜下方为终点的路径的和的较小值 + 当前a(i,j)的值
边界判断:第0行肯定要先独立的初始化,因为要用到i-1嘛;
正下方,当j<i时才能用(比如每行最后1个j==i就不能用了)
斜下方,当j>=1时才能用(比如每行第一个j==0时就不能由左斜下方推过来了)
最后的答案:由集合属性知,应输出第n-行也就是最后一行中的各个路径终点,所对应的最小值

class Solution {
public:
int minimumTotal(vector<vector<int>>& triangle) {
if(triangle.size() == 0) return 0;
int n = triangle.size();
int m = triangle[n-1].size();
int f[n][m];
f[0][0] = triangle[0][0];
for(int i=1;i<n;i++){
for(int j=0;j<triangle[i].size();j++){
f[i][j] = INT_MAX;
if(j < i)
f[i][j] = f[i-1][j] + triangle[i][j];
if(j>=1)
f[i][j] = min(f[i][j],
f[i-1][j-1]+triangle[i][j]);
}
}
int ans = INT_MAX;
for(int i = 0; i < m;i++){
// cout<<f[n-1][i]<<" ";
ans = min(ans,f[n-1][i]);
}
return ans;
}
};
因为f[i] 只需要用到 上一层f[-1] 的结果 所以可以用滚动数组来优化空间
滚动数组的版本:只需要开2个空间f[2],用&1来滚动 比如00变成01 01 变成 00
10变成11 11变成 10 100变成 101 101 变成 100
class Solution {
public:
int minimumTotal(vector<vector<int>>& triangle) {
if(triangle.size() == 0) return 0;
int n = triangle.size();
int m = triangle[n-1].size();
int f[2][m];
f[0][0] = triangle[0][0];
for(int i=1;i<n;i++){
for(int j=0;j<triangle[i].size();j++){
f[i & 1][j] = INT_MAX;
if(j < i)
f[i & 1][j] =
f[i-1 & 1][j] + triangle[i][j];
if(j>=1)
f[i & 1][j] = min(f[i & 1][j],
f[i-1 & 1][j-1]+triangle[i][j]);
}
}
int ans = INT_MAX;
for(int i = 0; i < m;i++){
ans = min(ans,f[n-1 & 1][i]);
}
return ans;
}
};
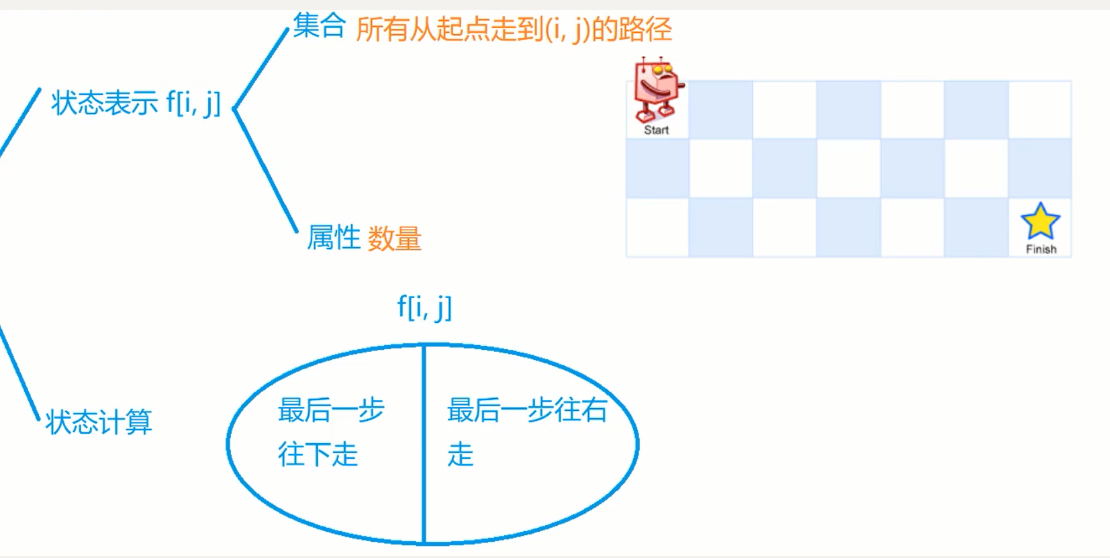
63. 不同路径 II
集合+属性:到达i,j的所有路径方案 的总个数
状态计算:不重复、不漏;
最后一步往下走:f(i,j) += f(i-1)(j) 当i>=1 并且f(i-1,j)能走到
最后一步往右走:f(I,j) += f(i,j-1) 当j>=1 并且f(i,j-1)能走到
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
int n = obstacleGrid.size();
int m = obstacleGrid[n-1].size();
vector<vector<int>> f(n,vector<int>(m,0));
if(obstacleGrid[n-1][m-1] == 1) return 0;
f[0][0] = 1;
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
if(obstacleGrid[i][j] == 1) f[i][j] = 0;
if(i>=1 && obstacleGrid[i-1][j] == 0){
f[i][j] += f[i-1][j];
}
if(j>=1 && obstacleGrid[i][j-1] == 0){
f[i][j] += f[i][j-1];
}
}
}
return f[n-1][m-1];
}
};
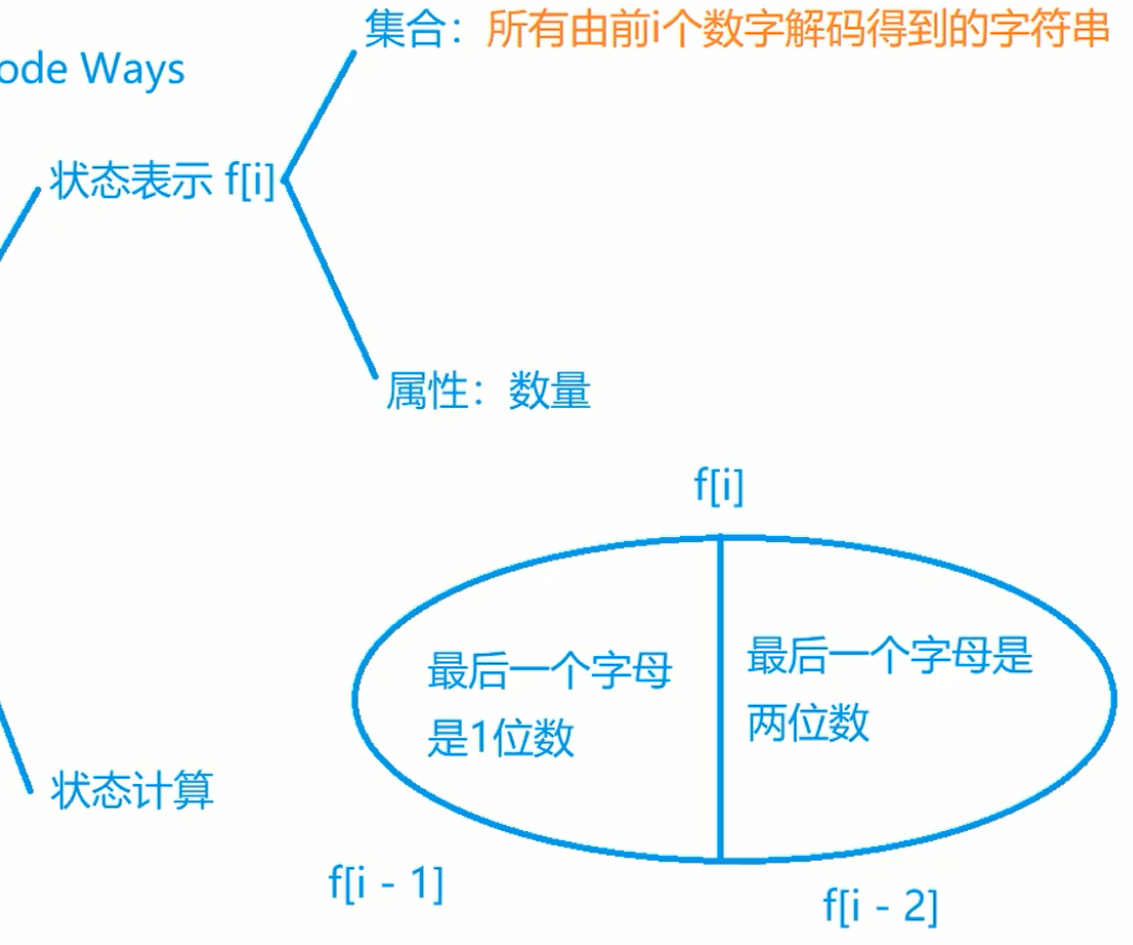
91. 解码方法
class Solution {
public:
int numDecodings(string s) {
int n = s.size();
vector<int> f(n+1);
f[0] = 1; //初始化
//注意从1开始算 因为是表示前多少个字母
for(int i=1;i<=n;i++){
if(s[i-1] != '0' ) f[i] += f[i-1];
if(i>=2){
int num = (s[i-2] - '0') * 10
+ (s[i-1]-'0');
if(num>=10 && num <= 26) f[i] += f[i-2];
}
}
return f[n];
}
};
198. 打家劫舍
假设偷盗经过了第i个房间时,那么有两种可能,偷第i个房间,或不偷第i个房间。如果偷得话,那么第i-1的房间一定是不偷的,所以经过第I个房间的最大值DP(i)=DP(I-2) +nums[i];如果经过第i房间不偷的话,那么经过第i房间时,偷取的最大值就是偷取前i-1房价的最大值。
这两种方案分别是dp[i-2]+nums[i]和 dp[i-1],取最大值就是经过第i房间的最大值
集合+属性:dp[i] 表示 到前i个房间为止所偷的方案 中的最大值
状态计算:考虑最后一个不同点,由两种子集推导过来
- 选第i个,dp[i] = dp[i-2] + nums[i];
- 不选第i个,dp[i] = dp[i-1];
class Solution {
public:
int rob(vector<int>& nums) {
int n = nums.size();
vector<int> dp(n);
int ans = 0;
if(n == 0) return 0;
if(n == 1) return nums[0];
//初始化边界
dp[0] = nums[0];
dp[1] = max(dp[0],nums[1]);
for(int i=2;i<n;i++){
//两种子集转移过来
dp[i] = max(dp[i-2] + nums[i],dp[i-1]);
}
for(int i=0;i<n;i++) ans = max(dp[i],ans);
return ans;
}
};
另一种思路:分成两个状态,选或者不选

最后结果为:max(f[n-1],g[n-1])

300. 最长上升子序列

class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int n = nums.size();
if(n == 0) return 0;
if(n == 1) return 1;
vector<int> f(n);
for(int i=0;i<n;i++) f[i] = 1;
for(int i=0;i<n;i++){
for(int j=0;j<i;j++){
if(nums[i] > nums[j]){
f[i] = max(f[i],f[j] + 1);
}
}
}
int ans = f[0];
for(int i=0;i<n;i++) ans = max(ans,f[i]);
return ans;
}
};
72. 编辑距离
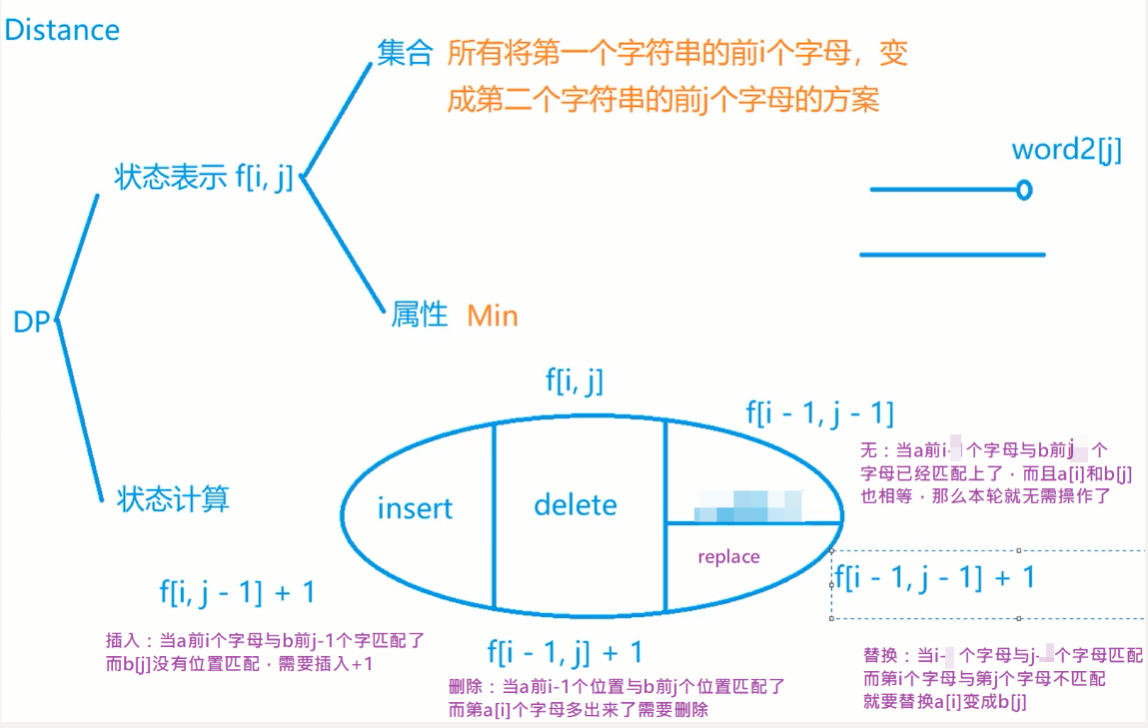
初始化:
1.把a前i个变成b前0个字母,需要删除i个;
2.把a前0个变成b前i个字母,需要插入i次;
class Solution {
public:
int minDistance(string word1, string word2) {
int n = word1.size();
int m = word2.size();
vector<vector<int>> f(n+1,vector<int>(m+1));
//初始化边界
for(int i=0;i<=n;i++) f[i][0] = i;
for(int i=0;i<=m;i++) f[0][i] = i;
//让i从1开始 表示前i个 前j个
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
//插入 和 删除
f[i][j] = min(f[i-1][j],f[i][j-1]) + 1;
//空 和 替换
if(word1[i-1] == word2[j-1]){
f[i][j] = min(f[i][j],f[i-1][j-1]);
}else f[i][j] = min(f[i][j],f[i-1][j-1] + 1);
}
}
return f[n][m];
}
};
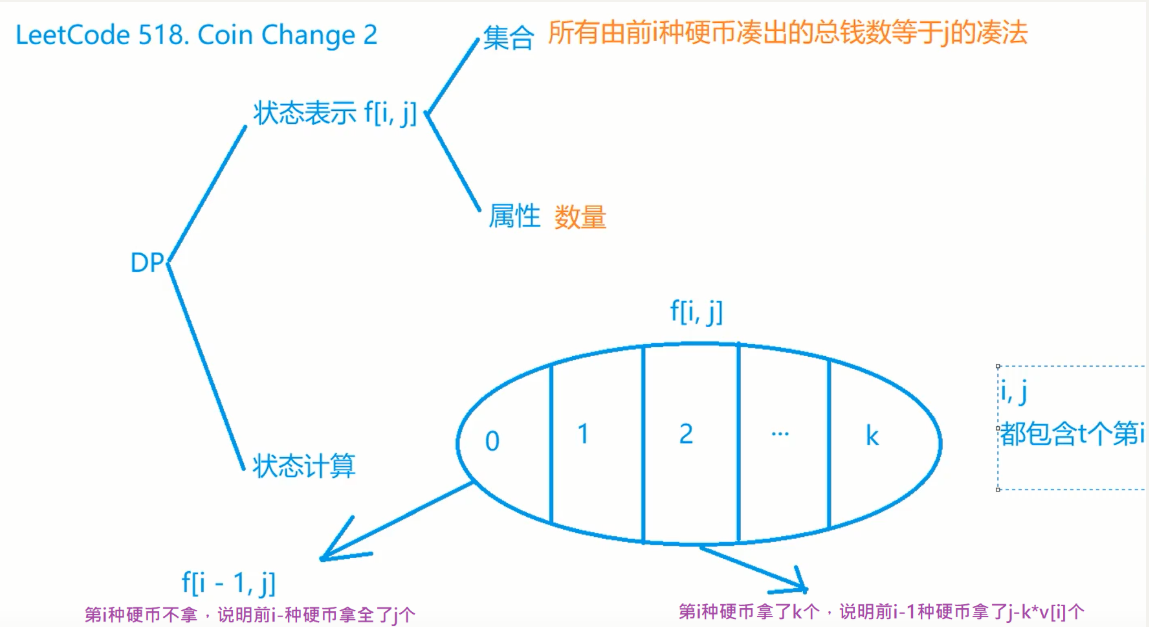
518. 零钱兑换 II
完全背包问题
三层循环

找状态之间的关系,优化到两层循环

优化成滚动数组,因为只会用到上一层和这一层前面的推导(正序从小到大推导)

边界f[0] = 1 凑0元也是一种方案
class Solution {
public:
int change(int amount, vector<int>& coins) {
int n = coins.size();
vector<int> f(amount+1);
f[0] = 1;
for(int i=0;i<n;i++){
for(int j=coins[i];j<=amount;j++){
f[j] += f[j-coins[i]];
}
}
return f[amount];
}
};
664. 奇怪的打印机
区间dp

状态计算:
- 之前只染色了左端点,
- 之前左半边染了LK个,并且能然LK个,那么S[k]必须和S[L]的颜色相同才会去染色,再加上右半边的染色最小值F[K+1,R]
class Solution {
public:
int strangePrinter(string s) {
if(s.empty()) return 0;
int n = s.size();
vector<vector<int>> f(n+1, vector<int>(n+1));
//枚举区间长度
for(int len = 1; len <= n ; len++){
//左端点
for(int l = 0;l + len - 1 < n ;l ++){
//右端点
int r = l + len - 1;
//1. 前一次只染色左端点
f[l][r] = f[l + 1][r] + 1;
//2. 前一次染色了 l~k
// 能染色的条件是因为s[k] = s[左端点]
for(int k = l + 1;k <= r; k ++){
if(s[k] == s[l]){
f[l][r] = min(f[l][r],f[l][k-1] + f[k+1][r]);
}
}
}
}
return f[0][n-1];
}
};
10. 正则表达式匹配

上面推导方案,需要枚举一遍 前面匹配的个数 O(n^3)
推导与f[i-1,j]的关系

可以看出,f[i,j]与f[i-1,j]比 多了一项判断条件:即s[i] 与 p[j-1]匹配
类似完全背包优化,寻找不同项之间的关系,相邻两项非常像,可以由前一项经过结合律来推导出



class Solution {
public:
bool isMatch(string s, string p) {
int n = s.length(), m = p.length();
vector<vector<bool>> f(n + 1, vector<bool>(m + 1, false));
s = " " + s;
p = " " + p;
f[0][0] = true;
for (int i = 0; i <= n; i++)
for (int j = 1; j <= m; j++) {
//1.当s[i]==p[j] || p[j] ==.时可从f[i-1][j-1]转移过来
if (i > 0 && (s[i] == p[j] || p[j] == '.'))
f[i][j] = f[i][j] | f[i - 1][j - 1];
//2.当P[j]时'*'
if (p[j] == '*') {
//当*表示匹配0个p[j-1]
//则可从f[i][j-2]即(p[j-2]字符)匹配过来
if (j >= 2)
f[i][j] = f[i][j] | f[i][j - 2];
//当*表示匹配了1个以上且最后1字符相等或.匹配
//则可以由f[i-1][j]匹配过来
//因为此时f[i-1][j]表示前i-1个s字符与前j个p字符能否匹配
//这个地方不太好看出来,就用推导相邻状态的方法推导处理
if (i > 0 && (s[i] == p[j - 1] || p[j - 1] == '.'))
f[i][j] = f[i][j] | f[i - 1][j];
}
}
return f[n][m];
}
};
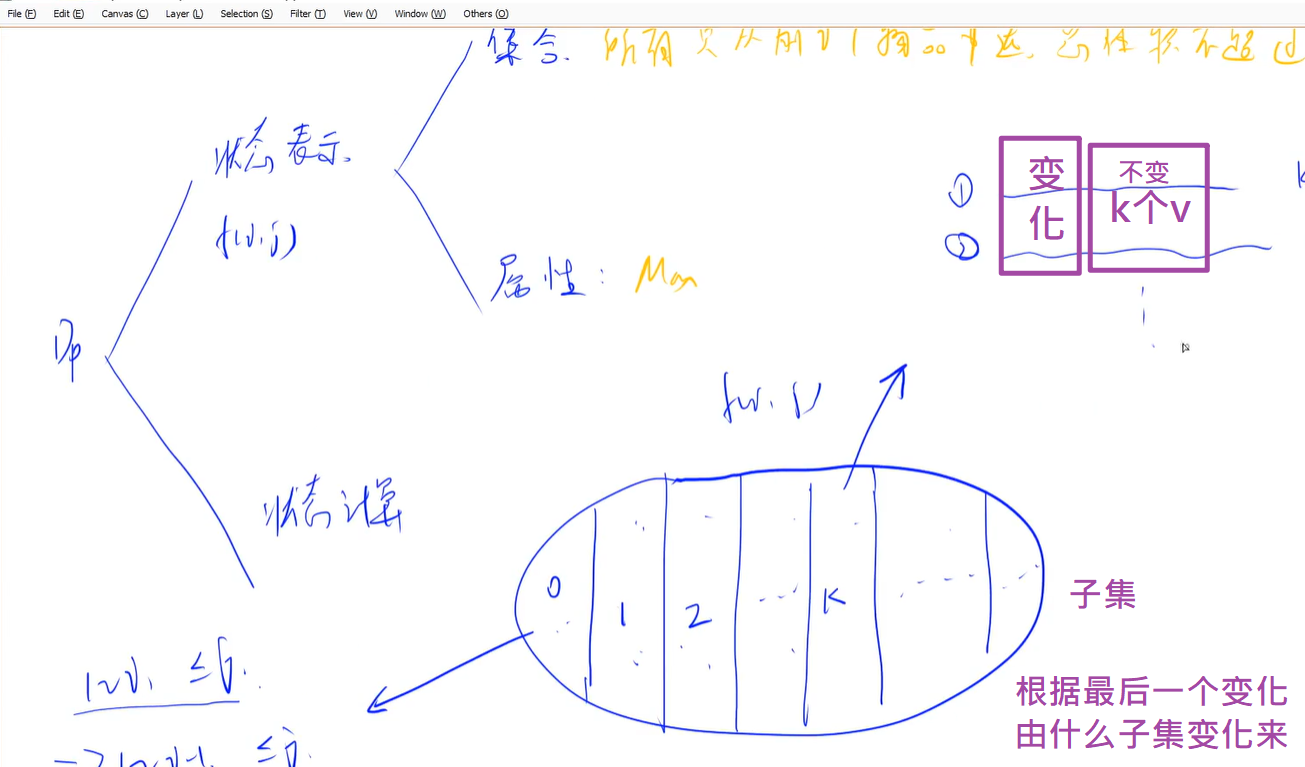
dp分析模型
01背包问题

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1010;
int w[MAXN],v[MAXN];
int n,m;
int f[MAXN];
/*
集合+属性: 所有只考虑前i个物品的选法的体积不超过j集合的最大价值
状态计算: f[i][j] = max (f[i-1][j], f[i-1][j-v[i]] + w[i] )
代码逻辑上的转移优化 一维:
f[j] = max(f[j], f[j-v[i]] + w[i] ) j从m到v[i]倒推
f[j-v[i]]就相当于 f[i-1][j-v[i]]
因为此时j>j-v[i] 此时推到了j 还没推到j-v[i]
*/
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
for(int i=1;i<=n;i++){
for(int j=m;j>=v[i];j--){
f[j] = max(f[j],f[j-v[i]] + w[i]);
}
}
cout<<f[m]<<endl;
return 0;
}
完全背包问题

根据相邻状态来优化dp转移方程

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1010;
int w[MAXN],v[MAXN];
int n,m;
int f[MAXN];
/*
集合+属性: 所有只拿前i个物品任意个数下的集合选法 的最大总价值
状态计算: f[i][j] = max(f[i-1][j] , f[i-1][j-v[i] + wi, f[i-1][j-v[i]*2]+2*w[i]...
状态优化: 因f[i][j-v[i]] = max(f[i-1][j-v[i]],f[i-1][j-v[i]*2] + w[i],f[i-1][j-v[i]*3] + w[i]*2
所以: f[i][j] = max(f[i-1][j] , f[i][j-v[i]] + w[i];
逻辑优化: 一维滚动
f[j] = max(f[j](上一轮), f[j-v[i]] + w[i] )
其中f[j-v[i]] 相当于 f[i][j-v[i]] 这一轮的j-v[i] 即j需要正序推导
*/
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
for(int i=1;i<=n;i++){
for(int j=v[i];j<=m;j++){
f[j] = max(f[j],f[j-v[i]] + w[i]);
}
}
cout<<f[m]<<endl;
return 0;
}
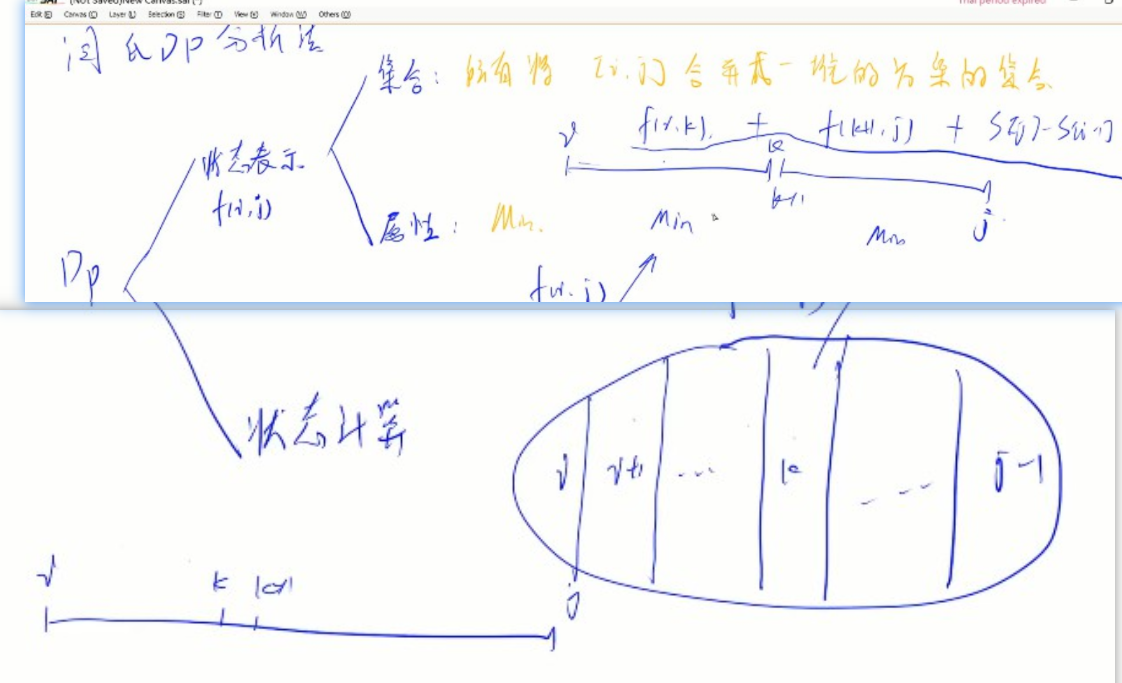
石子合并-区间dp模型
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 305;
int n;
int sum[MAXN],f[MAXN][MAXN];
/*
集合+属性: f[i][j] 所有i~j合并成一堆的方案的集合 的最小值
状态计算: 1.寻找最后一个不同点(每一堆石子都可由,左右两堆必须连续的推出)
2.找子集 f[i][j] = min(f[i][i] + f[i+1][j], f[i][i+2] + f[i+3][j])
f[i][j] = min(f[i][j], f[i][k] + f[k+1][j])
*/
int main(){
cin>>n;
for(int i=1;i<=n;i++) cin>>sum[i],sum[i] = sum[i] + sum[i-1];
for(int i=1;i<=n;i++) f[i][i] = 0;
for(int len=2;len<=n;len++){
for(int i=1;i+len-1<=n;i++){
int j = i+len-1;
f[i][j] = 1e8;
for(int k=i;k<j;k++){
f[i][j] = min(f[i][j],f[i][k] + f[k+1][j] + sum[j] - sum[i-1]);
}
}
}
cout<<f[1][n]<<endl;
return 0;
}
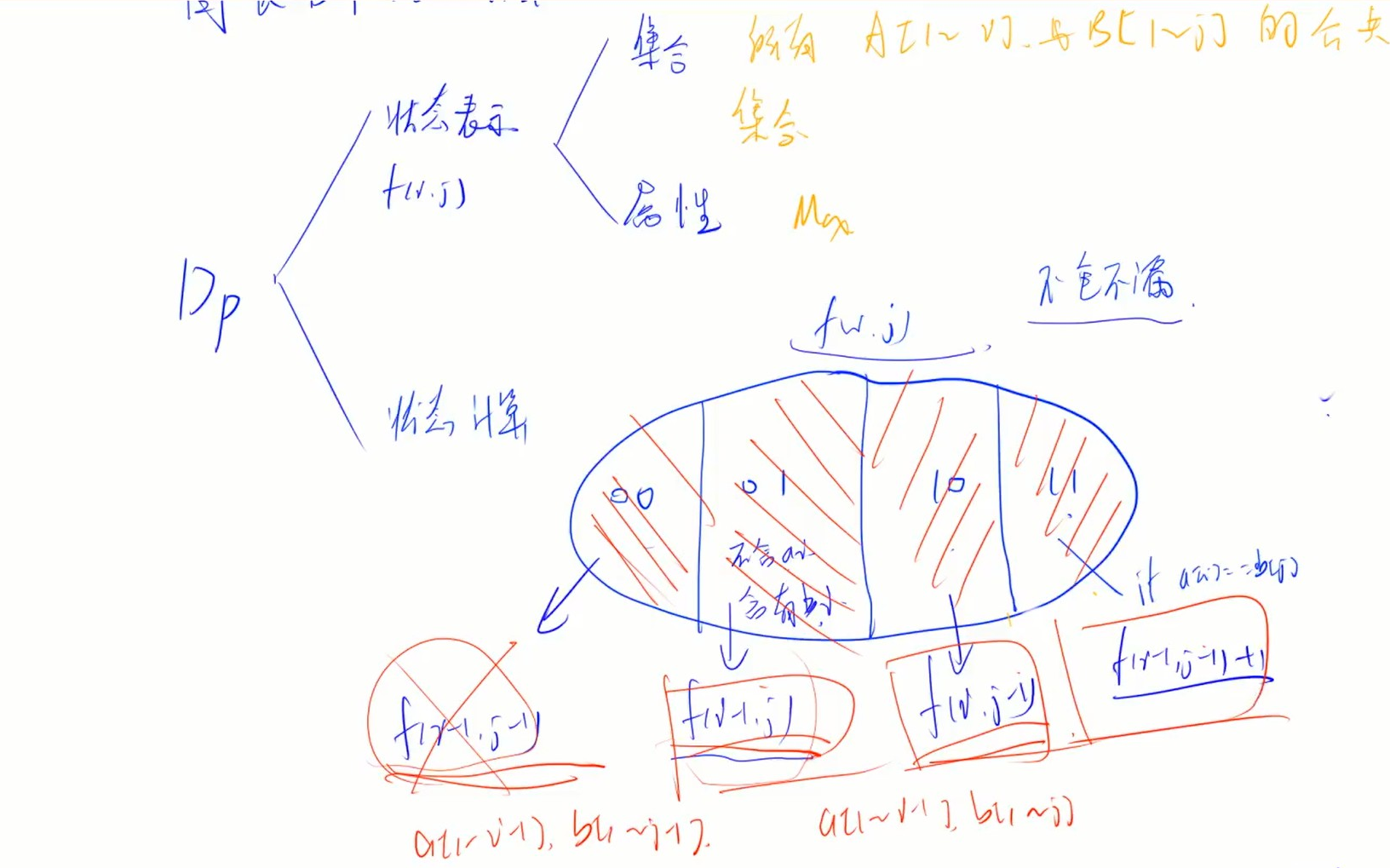
最长公共子序列-字符串序列模型
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1010;
char a[MAXN],b[MAXN];
int f[MAXN][MAXN];
int n,m;
/*
集合+属性: f[i][j] a前i个子序列与b前j个子序列的所有集合 中序列最长的长度
状态计算: 1.最后一个不同点: 2.找子集: 不重(求最值时可重) 不漏
a前i-1个 和 b前i-1个
a前i-1个 和 b前i个 -> 包含 a前i-1个 和 b前i-1个
a前i个 和 b前i-1个 -> 包含 a前i-1个 和 b前i-1个
a前i个 和 b前i个 (当a[i] = b[j] 时 = max(f[i][j],f[i-1][j-1] + 1)
f[i][j] = max(f[i][j], f[i-1][j], f[i][j-1], f[i-1][j-1] + 1)
*/
int main(){
cin>>n>>m>>a+1>>b+1;
f[0][0] = 0,f[1][0] = 0,f[0][1] = 0;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
f[i][j] = max(f[i][j-1],f[i-1][j]);
if(a[i] == b[j]) f[i][j] = max(f[i][j], f[i-1][j-1] + 1);
}
}
cout<<f[n][m]<<endl;
return 0;
}
小结
把dp问题看成 集合 变化(增大)转移的问题
集合 + 属性:最大/最小/总方案数/真假
状态计算:相当于当前集合的状态,是由几种集合状态推导而来;怎么找到由哪些推导出来的?寻找最后一个不同点,子集要求1.不重(最值可重方案不可重)、2.不漏;