PS:昨天月考,极其恶劣的成绩,结果李总在伤口上给我们撒盐,今天搞了个模拟赛~~~
1、期末考试
finaltest.cpp/c/pas
1s / 128M
[题目描述]
山山同学在期末考试前向他妈妈发誓,说自己能考到年级前10,他的妈妈不相信,但承诺道每一科他如果上了90分,她就可以奖励山山同学一些money。所以山山同学发奋复习,准备拿到最多的money去买他朝思暮想的东西。期末考试成绩下来了,山山立刻去看了成绩表,结果呢……
[输入描述]
输入文件finaltest.in一共m+3行。
第一行有1个整数m,表示了有多少个考试科目(英文小写的一个单词)。
接下来的m行中每行有三个数据:
第一个是科目。
第二个是考上90能拿的钱q(可能有最多2位的小数)。
第三个是他的这科成绩s。
接下来一行是他要买的东西的名称。
接下来还有一行,表示他买一个这样的东西需要的钱e。
[输出描述]
输出文件finaltest.out有两行。
第一行输出他一共能拿到的钱t(输出两位小数)。
第二行输出他能购买的量(整数),如果一个都没法买,就输出“ni wei he na me diao!”(输出不带引号)
[样例输入]
3
chinese 10 89
math 100.12 95
english 20 85
cassiopeia
69
[样例输出]
100.12
1
[数据范围]
数据保证有10%的数据m<=5。
数据保证有30%的数据不带小数。
数据保证100%的数据 0<m<1000 , 0<q<=10000,0<e<=1000000。
数据保证物品名全为英文小写。
Solution:
这道题,看了就呵呵~~送分(命)题,直接跑一遍模拟,对于分数大于等于90的便把钱加上,最后输出就行了。。。额,结果测出来65分,(神奇怎么会有错误呢?),一看数据,****科目名称竟然还有空格,处理一下,AC。
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cmath> 5 #include<cstring> 6 using namespace std; 7 int m;double tot,e; 8 string b; 9 int s;string k;double q; 10 inline int gi() //读入优化 11 { 12 int a=0;char x=getchar();bool f=0; 13 while((x>'9'||x<'0')&&x!='-')x=getchar(); 14 if(x=='-')f=1,x=getchar(); 15 while(x>='0'&&x<='9')a=a*10+x-48,x=getchar(); 16 return f?-a:a; 17 } 18 int main() 19 { 20 freopen("finaltest.in","r",stdin); 21 freopen("finaltest.out","w",stdout); 22 scanf("%d",&m); 23 for(int i=1;i<=m;i++){ //累加钱 24 cin>>k; 25 scanf("%lf",&q),s=gi(); 26 if(s>=90)tot+=q; 27 } 28 cin>>b>>e; 29 printf("%.2lf ",tot); 30 if(tot<e)printf("ni wei he na me diao!"); //太diao了 31 else printf("%d",(int)(tot/e)); 32 return 0; 33 }
2、买票
ticket.cpp/c/pas
1s /128M
[题目描述]
方老师在电影院卖票,有一新的电影上映,每张票的票价是5元,现在城里的支票有2种面值,5元和10元。如果一个人用5元的买票,那么方老师直接收下这5元,如果一个人用10元来买票,那么方老师会找给他一张5元。
方老师一开始有K张5元的支票,但如果某一刻时刻他没有5元的支票并且来了一个人持有10元的支票,那么方老师就会被打。
现在有N个人持有5元的支票和M个人持有10元的支票来买票,这N+M人的顺序不确定,问方老师有多大概率不会被打?
[输入描述]
输入文件ticket.in
三个数N,M,K分别表示有N个人持有5元的支票,M个人持有10元的支票,方老师一开始有K张5元的支票。
[输出描述]
输出文件ticket.out
一个数,表示概率,保留6位小数。
[样例输入]
5 3 1
[样例输出]
0.857143
[数据范围]
对于20%的数据,1 <= n, m <= 100
对于40%的数据,1 <= n, m <= 1000
对于100%的数据,1 <= n, m <= 100000, 0 <= k <= 10
Solution:
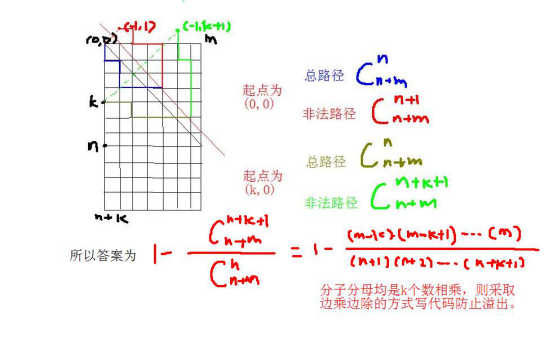
卡特兰数列的变形,本题把5元看做中有1,10元看做-1,起点在(k,0)处,要走到终点(n + k,m)处,不能超越从原点出发的对角线。
1 #include<iostream> 2 #include<cstdio> 3 using namespace std; 4 const int N = 100110; 5 const int INF = 1000000000; 6 const int Mod = 1000000007; 7 int n, m, K; 8 int main() 9 { 10 freopen("ticket.in","r",stdin); 11 freopen("ticket.out","w",stdout); 12 cin>>n>>m>>K; 13 double ans = 1; 14 if(n + K < m) 15 ans = 1; 16 else if(K >= m) 17 ans = 0; 18 else{ 19 for(int i=0; i < K + 1; i++){ 20 ans *= 1.0 * (m - i) / (n + K + 1 - i); 21 } 22 } 23 printf("%.6f ", 1 - ans); 24 return 0; 25 }
3、乘方
math.cpp/c/pas
1s / 128M
[题目描述]
求 2^x % y的值,即求2的x次幂除以y的余数。
[输入描述]
输入文件math.in
一行两个整数 x 和 y,用空格隔开
[输出描述]
输出文件math.out
一行一个整数,最后的答案
[样例输入]
3 3
[样例输出]
math.out
2
[数据范围]
对于 10%的数据: x<=2^6 – 1
对于 20%的数据: x<=2^17 – 1
对于 40%的数据: x<=2^64 – 1
对于 70%的数据: x<=2^333 – 1
对于 100%的数据: x<=2^233333 – 1 , y 为 [3,1000] 的质数
Solution:
40 分很容易,直接用 long long + 快速幂。
70分也不难,直接高精度。如果你写的高精度,但是还没得到 70 分,那就说明你没有压位(想想高精度相当于是循环
啊!)
100 分算法:费马小定理+快速幂
2^a%mod = (2^(a%(mod-1))%mod
大家可以找找规律,
令 y=3, x=0, 1, 2, 3, 4, …
令 y=5, x=0, 1, 2, 3, 4, …
令 y=7, x=0, 1, 2, 3, 4, …
令 y=11, x=0, 1, 2, 3, 4, …
……
大家可以发现余数是呈周期性变化的,周期为 y – 1
所以上面的等式就可以简单证明了(严格证明的话要用费马小定理)
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 using namespace std; 5 #define ll long long 6 ll x,y,m=2,cnt,a[100005],n; 7 inline void gi() 8 { 9 char i=getchar(); 10 while(i<'0'||i>'9')i=getchar(); 11 while(i>='0'&&i<='9'){a[++cnt]=i-'0';i=getchar();} 12 scanf("%lld",&y); 13 } 14 inline ll f(ll k) 15 { 16 ll res=1; 17 while(k) 18 { 19 if(k&1)res=res*m%y; 20 m*=m;m%=y; 21 k>>=1; 22 } 23 return res; 24 } 25 int main() 26 { 27 freopen("math.in","r",stdin); 28 freopen("math.out","w",stdout); 29 gi(); 30 for(int i=1;i<=cnt;i++) 31 n=(n*10+a[i])%(y-1); 32 printf("%lld",f(n)); 33 return 0; 34 }
4、帕秋莉•诺蕾姬
patchouli.cpp/c/pas
1s / 128M
[题目描述]
在幻想乡,帕秋莉•诺蕾姬是以宅在图书馆闻名的魔法使。这一天帕秋莉又在考虑如何加强魔法咒语的威力。帕秋莉的魔法咒语是一个仅有大写字母组成的字符串,我们考虑从’A’到’Z’分别表示0到25的数字,于是这个魔法咒语就可以看作一个26进制数。帕秋莉通过研究发现,如果一个魔法咒语所代表的数能够整除10进制数M的话,就能够发挥最大的威力。若当前的魔法咒语并不能整除M,帕秋莉只会将其中两个字符的位置交换,尽量让它能够被M整除,当然由于某些咒语比较特殊,无论怎么改变都不能达到这个目的。请你计算出她能否只交换两个字符就让当前咒语被M整除。(首位的’A’为前导0)
[输入描述]
输入文件一共2行。
第1行为1个字符串,长度不超过L。
第2行为1个正整数M。
[输出描述]
输出文件只有一行。
第1行为用空格隔开的2个整数,输出时先输位置靠前的那个。
如果存在多种交换方法,输出字典序最小的,比如1 3和1 5都可以达到目的,就输出1 3;1 3和2 4都行时也输出1 3。注意字符串下标从左到右依次为1到L开始。如果初始魔法咒语已经能够整除M,输出”0 0”;若无论如何也不能到达目的输出”-1 -1”。
[输入样例]
PATCHOULI
16
[输出样例]
4 9
[数据范围]
数据保证30%的数据:1 <= L <= 10, 1 <= M <= 100
数据保证50%的数据:除前面30%外,1 <= L <= 500, M = 5或25或26
数据保证100%的数据:1 <= L <= 2,000, 1 <= M <= 200,000
Solution:
1、乱搞出来的75分。30%的数据直接转换进制暴力码,50%的数据进行特判,去掉5或25或26的倍数什么的,就是随便弄一下就好了。先转换成一个10进制数,并且这个10进制数是小于2^63-1的。枚举每一对字母进行交换,若当前字符串所对应的10进制数能够整除M,输出即可。在算法一的基础上加上对5,25,26的特判:对于5,25只要各位数字之和能够被5或25整除,则该数能够5或25整除,否则无解;对于26,只需判断字符串内是否有’A’,无’A’则无解,否则只需把’A’换至最后一位,就能被26整除。
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cstring> 5 #define ll long long 6 using namespace std; 7 const int MAXL=2000+5; 8 char L[MAXL];int l,M; 9 int get_L() 10 { 11 int x=0; 12 for(int i=1;i<=l;i++) 13 x*=26,x+=L[i]-'A',x%=M; 14 return x%M; 15 } 16 void xfs() 17 { 18 if(!get_L()){puts("0 0");return;} 19 for(int i=1;i<l;i++) 20 { 21 for(int j=i+1;j<=l;j++) 22 { 23 swap(L[i],L[j]); 24 if(!get_L()) 25 {printf("%d %d ",i,j);return;} 26 swap(L[i],L[j]); 27 } 28 } 29 puts("-1 -1"); 30 return; 31 } 32 int main() 33 { 34 freopen("patchouli.in","r",stdin); 35 freopen("patchouli.out","w",stdout); 36 scanf("%s%d",L+1,&M); 37 l=strlen(L+1); 38 if(M==26) 39 { 40 if(L[l]=='A'){puts("0 0");return 0;} 41 for(int i=1;i<=l;i++) 42 if(L[i]=='A'){printf("%d%d ",i,l);return 0;} 43 puts("-1 -1"); 44 return 0; 45 } 46 if(M==5) 47 { 48 if(L[l]-'A'%5==0) 49 {puts("0 0");return 0;} 50 for(int i=1;i<=l;i++) 51 if(L[i]-'A'%5==0){printf("%d %d ",i,l);return 0;} 52 puts("-1 -1"); 53 return 0; 54 } 55 if(M==25) 56 { 57 int ans1=10000,ans2=10000; 58 if(L[l-1]-'A'==0||L[l-1]-'A'==2||L[l-1]-'A'==5||L[l-1]-'A'==7) 59 if(L[l]-'A'==5||L-'A'==0) 60 {puts("0 0");return 0;} 61 if(L[l]-'A'==5||L[l]-'A'==0) 62 { 63 for(int i=1;i<l;i++) 64 if(L[i]-'A'==0||L[i]-'A'==2||L[i]-'A'==5||L[i]-'A'==7) 65 {ans1 = i;break;} 66 } 67 if(L[l-1]-'A'==0||L[l-1]-'A'==2||L[l-1]-'A'==5||L[l-1]-'A'==7) 68 { 69 for(int i=1;i<l-1;i++) 70 if(L[i]-'A'==0||L[i]-'A'==5) 71 {ans2=i;break;} 72 } 73 if(ans1<ans2) 74 {printf("%d %d ",ans1,l-1);return 0;} 75 if(ans2<ans1) 76 {printf("%d %d ",ans2,l);return 0;} 77 puts("-1 -1"); 78 return 0; 79 } 80 xfs(); 81 return 0; 82 }
2、Jeff搞出来的90分。直接暴力枚举,两层循环交换第几个点。这里不多说,毕竟我没写~~
3、正解 100分。建立一个新的数组v[],v[i]=26^(i-1) mod M,将v[1..L]作为右数第1..L位的新权值,最后计算每一位的数字与它对应的新权值之积的和,即:
Sum = SUM{ num[i]*v[i] | 1 <= i <= N }
如果Sum能够整除M,则原26进制能够整除M。剩下的事就是枚举每一对字母进行交换,再进行判断。公式如下:
NewSum = Sum–num[i]*v[i]-num[j]*v[j]+num[i]*v[j]+num[j]*v[i]
1 /* 2 直接附上std代码非手打 3 */ 4 #include <iostream> 5 #include <cstdio> 6 using namespace std; 7 #define MAXL 1024 8 char str[MAXL]; 9 int fir[MAXL], rest[MAXL]; 10 int L,MOD; 11 12 void init() 13 { 14 freopen("patchouli.in","r",stdin); 15 freopen("patchouli.out","w",stdout); 16 } 17 18 void readdata() 19 { 20 scanf("%s", str); 21 scanf("%d", &MOD); 22 } 23 24 void work() 25 { 26 L=0;//对L初始化 27 for (int i=0;str[i];i++)//将咒语转换为26进制数 28 fir[++L]=str[i]-'A';//循环记录下每个字符代表的数 29 long long tp,sum=0; 30 rest[L]=1,sum=fir[L]; 31 for (int i=L-1;i>=1;i--)//取模的优化(降低难度) 32 { 33 rest[i]=(rest[i+1]*26)%MOD;//将26进制数转换为10进制 34 sum+=rest[i]*fir[i]; 35 }//计算每一位的数字与它对应的权值之积的和,最后取得能否被MOD整除 36 if (sum%MOD==0) printf("0 0 "); 37 else 38 {//不能整除就一个一个试,直到解决问题。 39 int x,y,ans_x,ans_y; 40 bool flag=false; 41 for (x=1;x<L&&!flag;x++) 42 for (y=x+1;y<=L&&!flag;y++)//将xy换位置得到新的sum 43 { 44 tp=sum-rest[x]*fir[x]-rest[y]*fir[y]; 45 tp+=rest[x]*fir[y]+rest[y]*fir[x]; 46 //公式自己推 47 //newsum = sum-num[i]*fir[i]-num[j]*fir[j]+num[i]*fir[j]+num[j]*fir[i] 48 if (tp%MOD==0)//判断新的sum能否满足条件 49 { 50 ans_x=x, ans_y=y; 51 flag=true; 52 } 53 } 54 if (!flag) ans_x=ans_y=-1;//如果还是不能解决,那就-1 -1吧。 55 printf("%d %d ",ans_x,ans_y); 56 } 57 } 58 59 int main() 60 { 61 init(); 62 readdata(); 63 work(); 64 return 0; 65 }
5、比赛
(match.pas/c/cpp)
1s / 128M
【问题描述】
山山非常喜欢看足球赛,但因为沉迷于刷集训队作业,错过了最近的一次足球联赛。此次联赛共n支球队参加,比赛规则如下:
(1) 每两支球队之间踢一场比赛。
(2) 若平局,两支球队各得1分。
(3) 否则胜利的球队得3分,败者不得分。
尽管非常遗憾没有观赏到精彩的比赛,但山山通过新闻知道了每只球队的最后总得分,然后聪明的他想计算出有多少种可能的比赛过程。
譬如有3支球队,每支球队最后均积3分,那么有两种可能的情况:
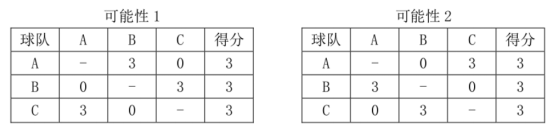
但山山发现当球队较多时,计算工作量将非常大,所以这个任务就交给你了。请你计算出可能的比赛过程的数目,由于答案可能很大,你只需要输出答案对10^9+7取模的结果。
【输入】
输入文件match.in。
第一行是一个正整数 n,表示一共有 n 支球队。
接下来一行 n 个非负整数,依次表示各队的最后总得分。
【输出】
输出文件match.out。
包含一个整数,表示答案对 10 9 +7 取模的结果。
【输入输出样例】
|
match.in |
match.out |
|
4 4 3 6 4 |
3
|
【数据说明】
20%:n≤4;
40%:n≤6;
60%:n≤8;
100%:n≤10 且至少存在一组解。
Solution:
(懒得自己写了,正解解析)
HNOI2013比赛:记忆化搜索。如果我们直接进行暴力搜索的话,会出现若干重复的情况,那么这个时候我们需要进行判重性剪枝,最直接的方式就是记录已经走过的状态。状态固然是当前每个队伍的得分,因为n<=10,但是即便这么小也不能直接存储,这里我们加一个long long的哈希来存储,开map进行判重。为什么这么暴力的办法是可行的?我们对状态数量进行一下分析就可以大胆使用了。10个队,对于每个队,最多比9场,得27分,那么放入hash函数中,最大为7.77*10^12,在long long范围内,用map存一下就行了。
搜索的过程也是有讲究的。我们将每支队伍的得分从大到小排序,将得分多的队伍优先进行搜索,每次与当前得分最低的队伍进行匹配,这样可以很快搜完。
1 #include <cstdio> 2 #include <algorithm> 3 #include <map> 4 using namespace std; 5 6 #define MAXN 15 7 #define MOD 1000000007 8 9 typedef long long ll; 10 11 struct Cmp 12 { 13 bool operator () (int a, int b) 14 { 15 return a > b; 16 } 17 }; 18 Cmp x; 19 20 ll a[MAXN]; 21 22 map <ll, ll> mp; 23 24 ll hash(int o) 25 { 26 ll res = o, tmp[MAXN]; 27 for (int i = 1; i <= o; i++) tmp[i] = a[i]; 28 sort(tmp + 1, tmp + o + 1, x); 29 for (int i = 1; i <= o; i++) res += res * 28 + tmp[i]; 30 return res; 31 } 32 33 ll DFS(int o, int n) 34 { 35 if (a[n] > 3 * (n - o)) return -1; 36 ll res = 0; 37 if (o == n) 38 { 39 if (n == 1) return 1; 40 else 41 { 42 ll h = hash(n - 1); 43 if (mp[h]) return mp[h]; 44 return mp[h] = DFS(1, n - 1); 45 } 46 } 47 if (a[n] >= 3) 48 { 49 ll tmp = 0; 50 a[n] -= 3, tmp = DFS(o + 1, n); 51 if (tmp != -1) (res += tmp) %= MOD; 52 a[n] += 3; 53 } 54 if (a[n] && a[o]) 55 { 56 ll tmp = 0; 57 a[n]--, a[o]--, tmp = DFS(o + 1, n); 58 if (tmp != -1) (res += tmp) %= MOD; 59 a[n]++, a[o]++; 60 } 61 if (a[o] >= 3) 62 { 63 ll tmp = 0; 64 a[o] -= 3, tmp = DFS(o + 1, n); 65 if (tmp != -1) (res += tmp) %= MOD; 66 a[o] += 3; 67 } 68 return res ? res : -1; 69 } 70 71 int n; 72 73 int main() 74 { 75 freopen("match.in", "r", stdin); 76 freopen("match.out", "w", stdout); 77 scanf("%d", &n); 78 for (int i = 1; i <= n; i++) scanf("%d", &a[i]); 79 sort(a + 1, a + n + 1, x); 80 printf("%d", DFS(1, n)); 81 return 0; 82 }