题目描述
栋栋有一块长方形的地,他在地上种了一种能量植物,这种植物可以采集太阳光的能量。在这些植物采集能量后,栋栋再使用一个能量汇集机器把这些植物采集到的能量汇集到一起。
栋栋的植物种得非常整齐,一共有n列,每列有m棵,植物的横竖间距都一样,因此对于每一棵植物,栋栋可以用一个坐标(x, y)来表示,其中x的范围是1至n,表示是在第x列,y的范围是1至m,表示是在第x列的第y棵。
由于能量汇集机器较大,不便移动,栋栋将它放在了一个角上,坐标正好是(0, 0)。
能量汇集机器在汇集的过程中有一定的能量损失。如果一棵植物与能量汇集机器连接而成的线段上有k棵植物,则能 量的损失为2k + 1。例如,当能量汇集机器收集坐标为(2, 4)的植物时,由于连接线段上存在一棵植物(1, 2),会产生3的能量损失。注意,如果一棵植物与能量汇集机器连接的线段上没有植物,则能量损失为1。现在要计算总的能量损失。
下面给出了一个能量采集的例子,其中n = 5,m = 4,一共有20棵植物,在每棵植物上标明了能量汇集机器收集它的能量时产生的能量损失。
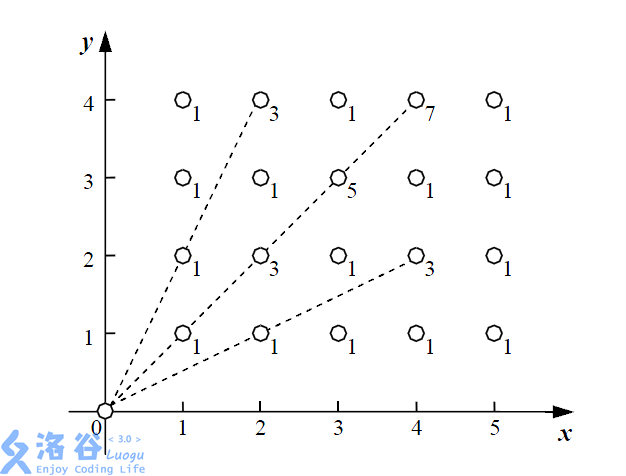
在这个例子中,总共产生了36的能量损失。
输入输出格式
输入格式:
仅包含一行,为两个整数n和m。
输出格式:
仅包含一个整数,表示总共产生的能量损失。
输入输出样例
说明
对于10%的数据:1 ≤ n, m ≤ 10;
对于50%的数据:1 ≤ n, m ≤ 100;
对于80%的数据:1 ≤ n, m ≤ 1000;
对于90%的数据:1 ≤ n, m ≤ 10,000;
对于100%的数据:1 ≤ n, m ≤ 100,000。
Solution:
本题zyys。
我们首先对图进行下分析,不难发现本题所求的是:$sumlimits_{i=1}^{n}sumlimits_{j=1}^{m}{gcd(i,j) imes 2 - 1}$。
直接暴力枚举显然行不通,但是不难发现,同一最小公约数$x$可能会出现多次,于是我们考虑求满足$ileq n,jleq m$的$gcd(i,j)=x$的个数$f[x]$,那么$x$对答案的贡献就是$f[x] imes (x imes 2 -1)$。
那么显然$1leq gcd(i,j)leq min(n,m)$,直接枚举每个最小公约数$x$,那么$n$内的是$x$的倍数的数至少有$lfloor{n/x} floor$个,同理$m$内有$lfloor{m/x} floor$个,那么$x$作为公约数的数对共$lfloor{n/x} floor imes lfloor{m/x} floor$个,由于要求的是最小公约数$x$,显然上述数对中存在最小公约数为$x$倍数的数对,所以我们由容斥原理直接从上面的数对中减去最小公约数为$2 imes x,3 imes x,…k imes x;,k imes xleq min(n,m)$的数对个数。
由于上面$x$的倍数都大于$x$,可以在枚举$x$之前处理,直接倒序循环就好了。
最后统计累加答案。显然时间复杂度为调和级数,$O(nlog n)$。
代码:
#include<bits/stdc++.h> #define il inline #define ll long long #define For(i,a,b) for(ll (i)=(a);(i)<=(b);(i)++) #define Bor(i,a,b) for(ll (i)=(b);(i)>=(a);(i)--) using namespace std; const int N=100005; ll n,m,f[N],ans; il int gi(){ int a=0;char x=getchar(); while(x<'0'||x>'9')x=getchar(); while(x>='0'&&x<='9')a=(a<<3)+(a<<1)+x-48,x=getchar(); return a; } int main(){ n=gi(),m=gi(); if(n>m)swap(n,m); Bor(i,1,n){ f[i]=(n/i)*(m/i); for(ll j=2;j*i<=n;j++)f[i]-=f[i*j]; ans+=f[i]*(i*2-1); } cout<<ans; return 0; }