题目描述
四个等长的单词可以放在一起构成一个正方形,两个单词水平放置,两个竖直放置。水平单词只能从左往右读,竖直的单词只能从上往下读。四个角共用一个字母。 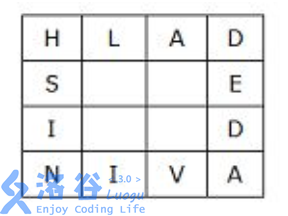
图中是由单词HLAD,NIVA,HSIN,DEDA构成的正方形。
你的任务是给你些等长的单词,请计算由这些单词能构成多少种不同的正方形。一个方案中不允许有同一个单词,两个方案不同是指它们所构成的正方形至少有一个字母不同。
输入输出格式
输入格式:第一行一个正整数 N(4≤N≤100000),表示单词的个数。
接下来 N 行,每行描述一个单词。单词由大写字母构成,且最多不超过 10个,所有单词都不相同且等长。
输出格式:一个数,表示不同的正方形的个数。答案保证不超过 64 位的正整数。
输入输出样例
输入样例#1:
4
NIVA
HLAD
HSIN
DEDA
输出样例#1:
2
输入样例#2:
6
BAKA
BARA
BALC
CALC
ARHC
BLIC
输出样例#2:
8
说明
20%的数据n≤30
50%的数据n≤10000
100%的数据n≤100000
Solution:
本题其实很水,直接暴力枚举就好了(今天一直在调昨天留下的ALADIN,只写了1题,实在没库存写博了,但又不想断更~)。
注意题目中的限制条件,保证单词均不相同,所以不用担心重复单词的情况。
那么组成正方形就只与首尾字母有关,于是我们开一个二维的桶记录每个首尾搭配出现的次数。
然后枚举3条边的情况,就能确定第4条边,累乘次数统计答案,而为了防止同一单词重复用,每次枚举一种首尾搭配后,该种搭配就-1,枚举完再补回来就好了。
时间复杂度$O(26^4)$。
代码:
/*Code by 520 -- 9.6*/ #include<bits/stdc++.h> #define ll long long #define RE register #define For(i,a,b) for(RE int (i)=(a);(i)<=(b);(i)++) using namespace std; int n,cnt[26][26]; ll ans; char s[15]; int main(){ scanf("%d",&n); For(i,1,n) scanf("%s",s),cnt[s[0]-'A'][s[strlen(s)-1]-'A']++; For(lup,0,25) For(rup,0,25) { int t1=cnt[lup][rup]--,t2,t3; For(ldo,0,25){ t2=cnt[lup][ldo]--; For(rdo,0,25){ t3=cnt[rup][rdo]--; ans+=(ll)cnt[ldo][rdo]*t1*t2*t3; cnt[rup][rdo]++; } cnt[lup][ldo]++; } cnt[lup][rup]++; } cout<<ans; return 0; }