【LeetCode-动态规划】完全平方数

题目描述

给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, ...）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。
示例：

输入: n = 12
输出: 3 
解释: 12 = 4 + 4 + 4.

输入: n = 13
输出: 2
解释: 13 = 4 + 9.

题目链接： https://leetcode-cn.com/problems/perfect-squares/

思路1

这题和零钱兑换本质是一样的，使用动态规划来做。

• 状态定义：dp[i] 表示组成和为 i 的完全平方数最小的个数，dp[i] 初始化为 i，表示由 i 个 1 的组成；
• 状态转移：dp[i] = min(dp[i], dp[i-j*j]+1), j 从 0 开始并且 i-j*j>=0；

代码如下：

class Solution {
public:
    int numSquares(int n) {
        if(n==0) return 0;

        vector<int> dp(n+1, 0);
        for(int i=0; i<dp.size(); i++) dp[i] = i;

        for(int i=1; i<=n; i++){
            for(int j=0; i-j*j>=0; j++){
                dp[i] = min(dp[i], dp[i-j*j]+1);
            }
        }
        return dp[n];
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(n)

思路2

使用 bfs。我们一层一层地添加节点，如果在添加某一层节点时，该节点为 0，说明我们已经找到了最短路径，返回该节点所在的层数即可。

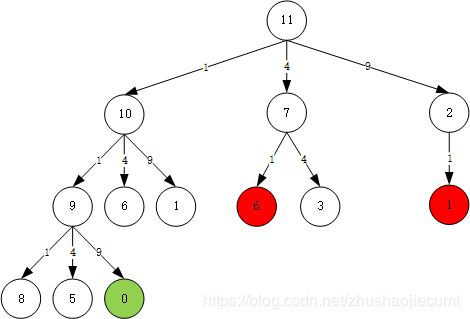
代码如下：

class Solution {
public:
    int numSquares(int n) {
        if(n==0) return 0;

        queue<int> q;
        unordered_set<int> visit;
        int level = 1;
        q.push(n);
        visit.insert(n);
        while(!q.empty()){
            int len = q.size();
            for(int i=0; i<len; i++){
                int cur = q.front(); q.pop();
                for(int j=1; j*j<=cur; j++){
                    int t = cur-j*j;
                    if(t==0) return level;
                    if(!visit.count(t)){
                        q.push(t);
                        visit.insert(t);
                    }
                }
            }
            level++;
        }
        return level;
    }
};