信息学竞赛常用函数/模板

说明：

1.模板中maxn表示最大数据规模，可以用   定义，其中数为数值

2.对于含有模板的模板，用类似于STL中的map，bitset的方法定义

数学模块

扩展欧几里得算法

说明：用于计算方程 其中 的一组解

void exgcd(int a,int b,int& d,int& x,int& y){
    if(!b){d=a,x=1,y=0;return;}
    exgcd(b,a%b,d,y,x);y-=x*(a/b);
}

　　

乘法逆元

说明：求a的模m乘法逆元（），其中a，m互质;如果返回值为-1说明无解，建议用参数类型用long long

void exgcd(int a,int b,int& d,int& x,int& y){
    if(!b){d=a,x=1,y=0;return;}
    exgcd(b,a%b,d,y,x);y-=x*(a/b);
}
int inverse(int a,int m){
	int x,y,d;
	exgcd(a,m,d,x,y);
	return d==1?(x%m+m)%m:-1;
}

　　

高精度模板

见：C ++中高精度正整数运算代码模板

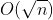计算欧拉函数

int phi(int x){
	int ans=x,m=sqrt(x+0.01);
	for(int i=2;i<=m;i++) if(x%i==0){
		ans=ans/i*(i-1);
		while(x%i==0) x/=i;
	}
	if(x>1) ans=ans/x*(x-1);//x为质数
	return ans;
}

　　

线性时间复杂度生成欧拉函数表+质数表

/* 
p|n &&  p*p|n phi(n)=phi(n/p)*p
p|n && !p*p|n phi(n)=phi(n/p)*(p-1) 
*/ 
int v[maxn],pri[maxn],phi[maxn];
void eular(int n){
	int num=0;//number of prime 
	for(int i=2;i<=n;i++) {
		if(v[i]==0){//v[i]:i 的最小质因子
			v[i]=i,pri[++num]=i;
			phi[i]=i-1;
		}
		for(int j=1;j<=num;j++){
			if(pri[j]>v[i]||pri[j]>n/i) break;
			v[i*pri[j]]=pri[j];
			phi[i*pri[j]]=phi[i]*(i%pri[j]?pri[j]-1:pri[j]);
		}
	}
	for(int i=1;i<=n;i++) printf("phi(%d)=%d
",i,phi[i]);
}

　　

BSGS算法

说明：用于计算高次同余方程   的最小非负数解，其中p为素数，时间复杂度，返回-1表示无解

int pow_mod(int a,int n,int p){
	int ret=1;
	while(n){
		if(n&1) ret=(long long)ret*a%p;
		a=(long long)a*a%p,n>>=1;
	}
	return ret;
}
map<int,int>mp;
int bsgs(int a,int b,int p){
	if(a%p==0) return b?-1:0;
	mp.clear();
	int m=ceil(sqrt(p)),T=b%p;
	mp[T]=0;
	for(int i=1;i<=m;i++)
		mp[T=(long long)T*a%p]=i;
	int t=pow_mod(a,m,p);T=1;
	for(int i=1;i<=m;i++){
		T=(long long)T*t%p;
		if(mp.count(T)) return i*m-mp[T];
	}
	return -1;
}

卢卡斯（Lucas）定理

说明：Lucas定理：若 p 为质数，对于整数有

代码中函数 C(N,M,p) 用于计算  ，inv[ i ] 表示 i 模 p 的逆元

int C(int N,int M,int p){
    if(N<M) return 0;
    if(!N) return 1;
    return (ll)fac[N]*inv[fac[M]]*inv[fac[N-M]]%p;
}
int lucas(int N,int M,int p){
    if(M==0) return 1;
    return (ll)lucas(N/p,M/p,p)*C(N%p,M%p,p)%p;
}

扩展中国剩余定理

说明：题目请参考：【模板】扩展中国剩余定理（EXCRT），算法请参考题解释：【模板】扩展中国剩余定理（EXCRT）题解

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=100005;
#define ll __int128
void exgcd(ll a,ll b,ll& d,ll& x,ll& y){
    if(!b){x=1,y=0,d=a;return;}
    exgcd(b,a%b,d,y,x),y-=x*(a/b);
}
ll gcd(ll a,ll b){
    return b?gcd(b,a%b):a;
}
ll lcm(ll a,ll b){
    return a*b/gcd(a,b);
}
ll a[maxn],b[maxn];
long long a__,b__;
int n;
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++) 
        scanf("%lld%lld",&a__,&b__),a[i]=a__,b[i]=b__;
    for(int i=1;i<n;i++){
        ll a_=a[i],b_=-a[i+1],c_=b[i+1]-b[i],d,x,y,md;
        exgcd(a_,b_,d,x,y);
        if(c_%d){break;/*No answer*/}
        x=c_/d*x,md=b_/d;
        if(md<0) md=-md;
        x=(x%md+md)%md;
        b[i+1]=a[i]*x+b[i];
        a[i+1]=lcm(a[i],a[i+1]);
    }
    printf("%lld
",(long long)b[n]);
    return 0;
}

矩阵运算

说明：T和MOD可以根据需要修改，其中unit_matrix（n）表示转化为n * n的单位矩阵

struct matrix{
	#define T int
	#define MOD 0x7fffffff
    int N,M;
	T mtx[maxn][maxn];
    matrix(){M=N=0;memset(mtx,0,sizeof(mtx));}
    void resize(int n,int m){N=n,M=m;}
    void unit_matrix(int n){
    	memset(mtx,0,sizeof(mtx));
    	N=M=n;
    	for(int i=0;i<n;i++) mtx[i][i]=1;
	}
    void input(){//just for int
        for(int i=0;i<N;i++)
          for(int j=0;j<M;j++)
            scanf("%d",&mtx[i][j]);
    }
    void output(){//just for int
        for(int i=0;i<M;i++){
        	for(int j=0;j<N;j++)
        		printf("%d ",mtx[i][j]);
        	putchar('
');
        }
    }
    friend matrix operator * (matrix x,matrix y){
        matrix ans;
    	if(x.N!=y.M) return ans; //Error
        ans.N=x.N,ans.M=y.M;
        for(int i=0;i<x.N;i++)
          for(int j=0;j<y.M;j++){
            T S=0;
            for(int k=0;k<x.N;k++)
                S=(S+x.mtx[i][k]*y.mtx[k][j])%MOD;
            ans.mtx[i][j]=S%MOD;
        }
        return ans;
    }
    friend matrix operator ^ (matrix x,int n){
    	matrix ans;
    	if(x.N!=x.M) return ans;//Error
    	ans.unit_matrix(x.N);
    	while(n){
    		if(n&1) ans=ans*x;
    		x=x*x,n>>=1;
		}
		return ans;
	}
    #undef T
    #undef MOD
};

数据结构模块

并查集

struct union_set{
	int f[maxn];
	void init(int n){for(int i=1;i<=n;i++) f[i]=i;}
	int find(int x){return x==f[x]?x:f[x]=find(f[x]);}
	bool merge(int x,int y){
		int fx=find(x),fy=find(y);
		if(fx!=fy) f[fx]=fy;
		return fx==fy;
	}
};

链表

数组版

struct node{
    int v,pre,nxt;
};
struct link_list{
    node E[maxn];
    int now,head,tail;
    link_list(){
        now=2,head=1,tail=2;
        E[head].nxt=tail,E[tail].pre=head;
    }
    int insert(int pos,int v){
        now++,E[now].v=v;
        E[E[pos].nxt].pre=now,E[now].nxt=E[pos].nxt;
        E[pos].nxt=now,E[now].pre=pos;
        return now;
    }
    int insert_to_tail(int v){
        return insert(E[tail].pre,v);
    }
    void del(int pos){
        E[E[pos].pre].nxt=E[pos].nxt;
        E[E[pos].nxt].pre=E[pos].pre;
    }
};

指针加强版

template<typename T>
struct node{
    T v;
    node *pre,*nxt;
};
template<typename T>
struct link_list{
    node<T> *head,*tail,*tmp;
	link_list(){
        head=new node<T>(),tail=new node<T>();
        head->nxt=tail,tail->pre=head;
    }
    node<T>* insert(node<T> *pos,T v){
        tmp=new node<T>();
        tmp->v=v;
        pos->nxt->pre=tmp,tmp->nxt=pos->nxt;
        pos->nxt=tmp,tmp->pre=pos;
        return tmp;
    }
    node<T>* insert_to_tail(T v){
        return insert(tail->pre,v);
    }
    node<T>* insert_to_head(T v){
        return insert(head,v);
    }
    void del(node<T>* pos){
        pos->pre->nxt=pos->nxt;
        pos->nxt->pre=pos->pre;
        delete pos;
    }
    node<T>* pre(node<T>* pos){return pos->pre;}
    node<T>* nxt(node<T>* pos){return pos->nxt;}
    T posv(node<T>* pos){return pos->v;}
    T prev(node<T>* pos){return pos->pre->v;}
    T nxtv(node<T>* pos){return pos->nxt->v;}
};

二叉堆

说明：比起优先队列，多了一个remove操作

template<typename T>
class Heap{
  private:
    T heap[maxn];
    int now;
  public:
    Heap(){now=0;}
    void up(int p){
        while(p){
          if(heap[p]<heap[p/2])
            swap(heap[p],heap[p/2]),p/=2;
          else break;
        }
    }
    void down(int p){
        int p_=p*2;
        while(p_<=now){
            if(p_<now&&heap[p_+1]<heap[p_]) p_++;
            if(heap[p_]<heap[p])
              swap(heap[p_],heap[p]),p=p_,p_*=2;
            else break;
        }
    }
    void push(T v){heap[++now]=v,up(now);}
    void pop(){heap[1]=heap[now--],down(1);}
    void remove(int p){heap[p]=heap[now--],up(p),down(p);}
    T top(){return heap[1];}
};

二维树状数组

说明：支持单点修改，区间求值

简易版

struct BIT_2{
  private:
  	#define lowbit(x) ((x)&-(x))
    int C[maxn][maxn];
  public:
  	void update(int x,int y,int d){
  		for(int i=x;i<=n;i+=lowbit(i))
  		  for(int j=y;j<=m;j+=lowbit(j))
  		    C[i][j]+=d;
    }
    int query(int x,int y){
        int ret=0;
        for(int i=x;i>0;i-=lowbit(i))
          for(int j=y;j>0;j-=lowbit(j))
            ret+=C[i][j];
        return ret;
    }
};

加强版

template<typename T,int N,int M>
class BIT_2{
  private:
  	#define lowbit(x) ((x)&-(x))
    T C[N+1][M+1],N_,M_;
  public:
  	BIT_2(){N_=N,M_=M;}
  	void reset(int n_,int m_){N_=n_,M_=m_;}
  	void update(int x,int y,int d){
  		for(int i=x;i<=N_;i+=lowbit(i))
  		  for(int j=y;j<=M_;j+=lowbit(j))
  		    C[i][j]+=d;
    }
    T query(int x,int y){
        T ret=0;
        for(int i=x;i>0;i-=lowbit(i))
          for(int j=y;j>0;j-=lowbit(j))
            ret+=C[i][j];
        return ret;
    }
    T query(int x,int y,int x_,int y_){
        return query(x_,y_)-query(x-1,y_)-query(x_,y-1)+query(x-1,y-1);
    }
};

Splay

Splay实现平衡树

模板题目见：【模板】普通平衡树，模板修改自洛谷日报，原文+详解见：Splay简易教程

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=100005;
int fa[maxn],ch[maxn][2],val[maxn],cnt[maxn],sz[maxn],rt,now;
int chk(int x){
    return ch[fa[x]][1]==x;
}
#define pushup(x) sz[x]=sz[ch[x][0]]+sz[ch[x][1]]+cnt[x]
void rotate(int x){
    int y=fa[x],z=fa[y],k=chk(x),w=ch[x][k^1];
    ch[y][k]=w,fa[w]=y;
    ch[z][chk(y)]=x,fa[x]=z;
    ch[x][k^1]=y,fa[y]=x;
    pushup(y),pushup(x);
}
void splay(int x,int goal=0){
    while(fa[x]!=goal){
        int y=fa[x],z=fa[y];
        if(z!=goal){
            if(chk(x)==chk(y)) rotate(y);
            else rotate(x);
        }
        rotate(x);
    }
    if(!goal) rt=x;
}
void rebuild(int x){//将小于等于x的最大元素重建到根
    int cur=rt;
    while(ch[cur][x>val[cur]]&&x!=val[cur])
        cur=ch[cur][x>val[cur]];
    splay(cur);
}
void insert(int x){
    int cur=rt,p=0;
    while(cur&&val[cur]!=x)
        p=cur,cur=ch[cur][x>val[cur]];
    if(cur) cnt[cur]++;
    else{
        cur=++now;
        if(p) ch[p][x>val[p]]=cur;
        ch[cur][0]=ch[cur][1]=0;
        val[cur]=x,fa[cur]=p;
        cnt[cur]=sz[cur]=1;
    }
    splay(cur);
}
int rank(int x){
    rebuild(x);
    return sz[ch[rt][0]];
}
int kth(int k){
    int cur=rt;
    while(true){
        if(ch[cur][0]&&k<=sz[ch[cur][0]])
            cur=ch[cur][0];
        else if(k>sz[ch[cur][0]]+cnt[cur])
            k-=sz[ch[cur][0]]+cnt[cur],cur=ch[cur][1];
        else return cur;
    }
}
int beside(int x,int pre){
    rebuild(x);
    if((val[rt]<x&&pre)||(val[rt]>x&&!pre)) return rt;
    int cur=ch[rt][pre^1];
    while(ch[cur][pre]) cur=ch[cur][pre];
    return cur;
}
void remove(int x){
    int pre=beside(x,1),nxt=beside(x,0);
    splay(pre),splay(nxt,pre);
    int cur=ch[nxt][0];
    if(cnt[cur]>1) cnt[cur]--,splay(cur);
    else ch[nxt][0]=0,sz[nxt]--,sz[pre]--;
}
int main(){
    int c,x,m;
    scanf("%d",&m);
    insert(0x3f3f3f3f);
    insert(-0x3f3f3f3f);
    while(m--){
    	scanf("%d%d",&c,&x);
    	switch(c){
    		case 1:insert(x);break;
    		case 2:remove(x);break;
    		case 3:printf("%d
",rank(x));break;
    		case 4:printf("%d
",val[kth(x+1)]);break;
    		case 5:printf("%d
",val[beside(x,1)]);break;
    		case 6:printf("%d
",val[beside(x,0)]);break;
        }
    }
    return 0;
}

Splay实现序列翻转

模板题目见：【模板】文艺平衡树（Splay）

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=100005;
int fa[maxn],ch[maxn][2],val[maxn],cnt[maxn],sz[maxn],rt,now;
int n,m,l,r,rev[maxn];
int chk(int x){
    return ch[fa[x]][1]==x;
}
void pushup(int x){
    sz[x]=sz[ch[x][0]]+sz[ch[x][1]]+cnt[x];
}
void pushdown(int x){
    if(!rev[x]) return;
    swap(ch[x][0],ch[x][1]);
    if(ch[x][0]) rev[ch[x][0]]^=1;
	if(ch[x][1]) rev[ch[x][1]]^=1;
    rev[x]=0;
}
void rotate(int x){
    int y=fa[x],z=fa[y],k=chk(x),w=ch[x][k^1];
    ch[y][k]=w,fa[w]=y;
    ch[z][chk(y)]=x,fa[x]=z;
    ch[x][k^1]=y,fa[y]=x;
    pushup(y),pushup(x);
}
void splay(int x,int goal=0){
    while(fa[x]!=goal){
        int y=fa[x],z=fa[y];
        pushdown(z),pushdown(y),pushdown(x);//在这道题里可以不要 
        if(z!=goal){
            if(chk(x)==chk(y)) rotate(y);
            else rotate(x);
        }
        rotate(x);
    }
    if(!goal) rt=x;
}
void insert(int x){
    int cur=rt,p=0;
    while(cur&&val[cur]!=x)
        p=cur,cur=ch[cur][x>val[cur]];
    if(cur) cnt[cur]++;
    else{
        cur=++now;
        if(p) ch[p][x>val[p]]=cur;
        ch[cur][0]=ch[cur][1]=0;
        val[cur]=x,fa[cur]=p;
        cnt[cur]=sz[cur]=1;
    }
    splay(cur);
}
int kth(int k){
    int cur=rt;
    while(true){
        pushdown(cur);
        if(ch[cur][0]&&k<=sz[ch[cur][0]])
            cur=ch[cur][0];
        else if(k>sz[ch[cur][0]]+cnt[cur])
            k-=sz[ch[cur][0]]+cnt[cur],cur=ch[cur][1];
        else return cur;
    }
}
void reverse(int l,int r){
    int x=kth(l),y=kth(r+2);
    splay(x),splay(y,x);
    rev[ch[y][0]]^=1;
}
void output(int x){
    pushdown(x);
    if(ch[x][0]) output(ch[x][0]);
    if(val[x]&&val[x]<=n) printf("%d ",val[x]);//要判断虚拟节点
    if(ch[x][1]) output(ch[x][1]);
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=0;i<=n+1;i++) insert(i);
    while(m--)
        scanf("%d%d",&l,&r),reverse(l,r);
    output(rt);
    return 0;
}

其他

对拍器

说明：写入记事本，保存为后缀名为 的文件，即可执行;其中randdata.exe为数据生成器，code1.exe code2.exe分别为测试程序与标准程序。

@echo off
for /l %%i in (1,1,100) do (
  randdata.exe > in.txt
  code1.exe < in.txt > out1.txt
  code2.exe < in.txt > out2.txt
  fc out1.txt out2.txt > result.txt
  if errorlevel 1 echo %%i:WA! && pause
  if not errorlevel 1 echo %%i:AC!
)
pause

快速输入输出（适用于非负整数）

char in_c;
template<typename T>
void scan(T &in_n){
	for(in_c=getchar();in_c<'0'||in_c>'9';in_c=getchar());
	for(in_n=0;in_c>='0'&&in_c<='9';in_c=getchar()) in_n=in_n*10+in_c-'0';
}
char out_c[25];
int sz_out_c;
template<typename T>
void print(T out_n){
	sz_out_c=0;
	if(!out_n) out_c[sz_out_c++]='0';
	while(out_n) out_c[sz_out_c++]=out_n%10+'0',out_n/=10;
	while(sz_out_c--) putchar(out_c[sz_out_c]);
}

 

---

主要参考资料：

1.《算法竞赛 - 进阶指南》 -李煜东

2.  我校信息学竞赛讲义       -Mr_He