一、术语解释
关联分析:从大规模数据集中挖掘物品之间的隐含关系
频繁项集:经常出现在一块的物品集合
关联规则:暗示两种物品之间可能存在很强的关联关系
项集支持度:数据集中包含该项集的记录比例(这里可以定义一个最小项集的支持度,筛选出那些项集出现次数不是那么多,项集支持度不是那么大的集合)
关联规则{a}->{b}置信度:{a,b}的支持度/{a}的支持度
二、目标与假设
假设商店有4中商品:0 1 2 3
而我们的目标是寻找那些商品会同时被购买,我们要做的是经常在一起购买的商品集合
如何计算频繁项集的支持度:计算有多少比例的交易记录包含该集合,那么我们就需要遍历每条交易记录,看他们是否同时包含该集合,如果包含,就count+1,最后利用count/总的交易记录数
那么4中商品,总的组合数为2的4次方-1,也就是需要遍历这么多次,那么面对商场里面那么多商品,如何简化呢
三、Apriori算法
Apriori原理:如果某个项集是频繁的,那么他的子集必定频繁,同理,如果一个项集是非频繁集,那么他的所有超集也是非频繁集
也就是说如果我们计算出的{0,1}的支持度很小很小,那么所有包含他的集合也就直接pass了
3.1找到频繁集
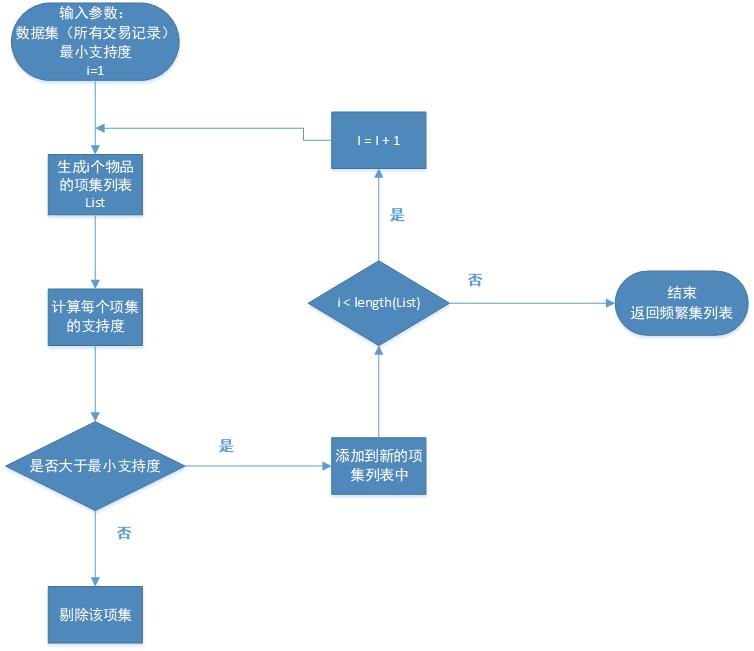
1、加载数据集
def loadDataSet():
return [[1, 3, 4], [2, 3, 5], [1, 2, 3, 5], [2, 5]][[1, 3, 4], [2, 3, 5], [1, 2, 3, 5], [2, 5]]2、遍历所有交易记录,返回单个无重复商品组成的候选项集
def createC1(dataSet):
C1 = []
for transaction in dataSet:
for item in transaction:
if not [item] in C1:
C1.append([item])
C1.sort()
#采用frozenset而不是set,是为了防止用户修改,可以作为字典的键
C1 = map(frozenset, C1)
return C1if __name__=="__main__":
dataSet = loadDataSet();
C1 = createC1(dataSet)
print(C1)
'''[frozenset({1}), frozenset({2}), frozenset({3}), frozenset({4}), frozenset({5})]'''
'''
[frozenset({1}), frozenset({2}), frozenset({3}), frozenset({4}), frozenset({5})]
'''3、筛选出支持度大于最小支持度的候选项集
#minSupport感兴趣项集的最小支持度
def scanD(D, Ck, minSupport):
ssCnt = {}
#遍历候选集和的列表
#遍历每条交易记录
#D=map(set,data)
for tid in D:
#遍历数据集
#遍历顾客购买的所有物品种类map(frozenset, C1)
for can in Ck:
#测试can的每个元素是否都在tid中
if can.issubset(tid):
if not can in ssCnt:
# if not ssCnt.has_key(can):
ssCnt[can]=1
else: ssCnt[can] += 1
#统计候选列表的长度
#交易次数
numItems = float(len(D))
retList = []
supportData = {}
#ssCnt记录每种物品的次数
for key in ssCnt:
#得到每种物品的支持度a
support = ssCnt[key]/numItems
#统计出所有物品的支持度大于最小支持度的物品放入列表retlist
if support >= minSupport:
#插入到头部
retList.insert(0,key)
supportData[key] = support
return retList, supportDataif __name__=="__main__":
data = loadDataSet()
C1 = [frozenset({1}), frozenset({2}), frozenset({3}), frozenset({4}), frozenset({5})]
retList, supportData = scanD(data, C1, 0.5)
print("retList:",retList)
print("supportData:",supportData)
'''retList: [frozenset({5}), frozenset({2}), frozenset({3}), frozenset({1})]
supportData: {frozenset({1}): 0.5, frozenset({3}): 0.75, frozenset({4}): 0.25, frozenset({2}): 0.75, frozenset({5}): 0.75}'''
4、两两组合,将单个集合组成含有两个元素的候选集
'''
Lk频繁项集列表
k项集元素个数
'''
def aprioriGen(Lk, k): #creates Ck
retList = []
lenLk = len(Lk)
for i in range(lenLk):
for j in range(i+1, lenLk):
print("循环")
#[:k-2]=[0:0] 为空
L1 = list(Lk[i])[:k-2];
print("Lk[i]:",Lk[i])
print("list(Lk[i]):",list(Lk[i]))
print( "list(Lk[i])[:k-2]:", L1)
L2 = list(Lk[j])[:k-2]
print("Lk[j]:",Lk[j])
print("list(Lk[j]):",list(Lk[j]))
print("list(Lk[j])[:k-2]:",L2)
L1.sort();
L2.sort()
if L1==L2: #if first k-2 elements are equal
retList.append(Lk[i] | Lk[j]) #set union
print("retList1:",retList)
return retList
if __name__ == '__main__':
Lk = [frozenset({5}), frozenset({2}), frozenset({3}), frozenset({1})]
retList = aprioriGen(Lk,2)
print("retList:",retList)
循环
Lk[i]: frozenset({5})
list(Lk[i]): [5]
list(Lk[i])[:k-2]: []
Lk[j]: frozenset({2})
list(Lk[j]): [2]
list(Lk[j])[:k-2]: []
retList1: [frozenset({2, 5})]
循环
Lk[i]: frozenset({5})
list(Lk[i]): [5]
list(Lk[i])[:k-2]: []
Lk[j]: frozenset({3})
list(Lk[j]): [3]
list(Lk[j])[:k-2]: []
retList1: [frozenset({2, 5}), frozenset({3, 5})]
循环
Lk[i]: frozenset({5})
list(Lk[i]): [5]
list(Lk[i])[:k-2]: []
Lk[j]: frozenset({1})
list(Lk[j]): [1]
list(Lk[j])[:k-2]: []
retList1: [frozenset({2, 5}), frozenset({3, 5}), frozenset({1, 5})]
循环
Lk[i]: frozenset({2})
list(Lk[i]): [2]
list(Lk[i])[:k-2]: []
Lk[j]: frozenset({3})
list(Lk[j]): [3]
list(Lk[j])[:k-2]: []
retList1: [frozenset({2, 5}), frozenset({3, 5}), frozenset({1, 5}), frozenset({2, 3})]
循环
Lk[i]: frozenset({2})
list(Lk[i]): [2]
list(Lk[i])[:k-2]: []
Lk[j]: frozenset({1})
list(Lk[j]): [1]
list(Lk[j])[:k-2]: []
retList1: [frozenset({2, 5}), frozenset({3, 5}), frozenset({1, 5}), frozenset({2, 3}), frozenset({1, 2})]
循环
Lk[i]: frozenset({3})
list(Lk[i]): [3]
list(Lk[i])[:k-2]: []
Lk[j]: frozenset({1})
list(Lk[j]): [1]
list(Lk[j])[:k-2]: []
retList1: [frozenset({2, 5}), frozenset({3, 5}), frozenset({1, 5}), frozenset({2, 3}), frozenset({1, 2}), frozenset({1, 3})]
retList: [frozenset({2, 5}), frozenset({3, 5}), frozenset({1, 5}), frozenset({2, 3}), frozenset({1, 2}), frozenset({1, 3})]
5、筛选出大于最小支持度的候选项
if __name__=="__main__":
data = loadDataSet()
C1 = [frozenset({2, 5}), frozenset({3, 5}), frozenset({1, 5}), frozenset({2, 3}), frozenset({1, 2}), frozenset({1, 3})]
retList, supportData = scanD(data, C1, 0.5)
print("retList:",retList)
print("supportData:",supportData)
'''retList: [frozenset({2, 3}), frozenset({3, 5}), frozenset({2, 5}), frozenset({1, 3})]
supportData: {frozenset({1, 3}): 0.5, frozenset({2, 5}): 0.75, frozenset({3, 5}): 0.5, frozenset({2, 3}): 0.5, frozenset({1, 5}): 0.25, frozenset({1, 2}): 0.25}
'''
下面就是将两个元素的集合组合成三个,那么我们通过一个函数来将这些步骤串起来
def apriori(dataSet, minSupport = 0.5):
#物品种类列表C1
#单个元素的候选项集
C1 = createC1(dataSet)
#交易记录集合
# D = map(set, dataSet)
#大于最小支持度的物品列表L1,以及物品对应的支持度supportData
#筛选出大于最小支持度的候选项集
L1, supportData = scanD(dataSet, C1, minSupport)
#候选项集列表
L = [L1]
k = 2
#大于最小支持度的物品列表L1的长度大于0
#L[k-2]=L[0]=L1
while (len(L[k-2]) > 0):
Lk_1 = L[k-2]
#得到物品列表L1之间的两两组合
#将候选项集组成2个元素的集合
Ck = aprioriGen(Lk_1, k)
print("Ck",Ck)
#得到大于最小支持度的集合Lk,以及对应支持度
Lk, supK = scanD(dataSet, Ck, minSupport)#scan DB to get Lk
#更新物品组合的支持度,直接添加在后面
supportData.update(supK)
print("Lk",Lk)
L.append(Lk)
#增加组合的元素个数
k += 1
return L, supportDataif __name__=="__main__":
data = loadDataSet()
L, supportData = apriori(data)
print("L-->",L)
print("supportData--->",supportData)L--> [[frozenset({5}), frozenset({2}), frozenset({3}), frozenset({1})], [frozenset({2, 3}), frozenset({3, 5}), frozenset({2, 5}), frozenset({1, 3})], [frozenset({2, 3, 5})], []]
supportData---> {frozenset({1}): 0.5, frozenset({3}): 0.75, frozenset({4}): 0.25, frozenset({2}): 0.75, frozenset({5}): 0.75, frozenset({1, 3}): 0.5, frozenset({2, 5}): 0.75,
frozenset({3, 5}): 0.5, frozenset({2, 3}): 0.5, frozenset({1, 5}): 0.25, frozenset({1, 2}): 0.25, frozenset({2, 3, 5}): 0.5}3.2从频繁项集中挖掘关联规则
对于只有一个元素的项集我们就不用考虑关联规则了,所以我们从二元项集开始挖掘每个项集中的元素之间的关联规则
1、先将每个二元项集转换为列表形式,然后每个元素为frozenset集合
def generateRules(L, supportData, minConf=0.7): #supportData is a dict coming from scanD
#包含置信度的规则列表
bigRuleList = []
#从频繁二项集开始遍历(一个元素的项集没有关联规则)
for i in range(1, len(L)):#only get the sets with two or more items
#遍历所有的二项集
for freqSet in L[i]:
#遍历每个二项集的元素,设置为frozenset集合
H1 = [frozenset([item]) for item in freqSet]
print(H1)if __name__ == '__main__':
L = [[frozenset({5}), frozenset({2}), frozenset({3}), frozenset({1})], [frozenset({2, 3}), frozenset({3, 5}), frozenset({2, 5}), frozenset({1, 3})], [frozenset({2, 3, 5})], []]
supportData = {frozenset({1}): 0.5, frozenset({3}): 0.75, frozenset({4}): 0.25, frozenset({2}): 0.75, frozenset({5}): 0.75, frozenset({1, 3}): 0.5, frozenset({2, 5}): 0.75,
frozenset({3, 5}): 0.5, frozenset({2, 3}): 0.5, frozenset({1, 5}): 0.25, frozenset({1, 2}): 0.25, frozenset({2, 3, 5}): 0.5}
generateRules(L,supportData)
'''
[frozenset({2}), frozenset({3})]
[frozenset({3}), frozenset({5})]
[frozenset({2}), frozenset({5})]
[frozenset({1}), frozenset({3})]
[frozenset({2}), frozenset({3}), frozenset({5})]
'''2、筛选出置信度符合要求的二项集
#计算是否满足最小置信度
'''
freqSet:每一个项集
H:项集的每个元素组成的集合
supportData:包含频繁项集支持度的字典
brl:包含置信度的规则列表
minConf=0.7:最小置信度
'''
def calcConf(freqSet, H, supportData, brl, minConf=0.7):
prunedH = [] #create new list to return
#遍历项集中的每个元素集合
for conseq in H:
# supportData[freqSet]计算该项集的支持度
# supportData[freqSet-conseq]计算该项集中每个元素的支持度
# conf得到由该项集推出该项集两两之间的关联规则的置信度
# freqSet-conseq因为都是frozenset集合,可以做减法
conf = supportData[freqSet]/supportData[freqSet-conseq] #calc confidence
#筛选出符合条件的关联规则
if conf >= minConf:
print (freqSet-conseq,'-->',conseq,'conf:',conf)
brl.append((freqSet-conseq, conseq, conf))
prunedH.append(conseq)
return brl,prunedH
if __name__ == '__main__':
freqSet = frozenset({2,5})
H =[frozenset({2}), frozenset({5})]
supportData = {frozenset({1}): 0.5, frozenset({3}): 0.75, frozenset({4}): 0.25, frozenset({2}): 0.75, frozenset({5}): 0.75, frozenset({1, 3}): 0.5, frozenset({2, 5}): 0.75,
frozenset({3, 5}): 0.5, frozenset({2, 3}): 0.5, frozenset({1, 5}): 0.25, frozenset({1, 2}): 0.25, frozenset({2, 3, 5}): 0.5}
brl=[]
brl,prunedH= calcConf(freqSet, H, supportData, brl, minConf=0.7)
print("br1",brl);
print("prunedH",prunedH)
'''frozenset({5}) --> frozenset({2}) conf: 1.0
frozenset({2}) --> frozenset({5}) conf: 1.0
br1 [(frozenset({5}), frozenset({2}), 1.0), (frozenset({2}), frozenset({5}), 1.0)]
prunedH [frozenset({2}), frozenset({5})]'''if __name__ == '__main__':
freqSet = frozenset({1,3})
H =[frozenset({1}), frozenset({3})]
supportData = {frozenset({1}): 0.5, frozenset({3}): 0.75, frozenset({4}): 0.25, frozenset({2}): 0.75, frozenset({5}): 0.75, frozenset({1, 3}): 0.5, frozenset({2, 5}): 0.75,
frozenset({3, 5}): 0.5, frozenset({2, 3}): 0.5, frozenset({1, 5}): 0.25, frozenset({1, 2}): 0.25, frozenset({2, 3, 5}): 0.5}
brl=[]
brl,prunedH= calcConf(freqSet, H, supportData, brl, minConf=0.7)
print("br1",brl);
print("prunedH",prunedH)
'''frozenset({1}) --> frozenset({3}) conf: 1.0
br1 [(frozenset({1}), frozenset({3}), 1.0)]
prunedH [frozenset({3})]''''''
freqSet:每一个项集
H:项集的每个元素组成的集合
supportData:包含频繁项集支持度的字典
brl:包含置信度的规则列表
minConf=0.7:最小置信度
'''
def rulesFromConseq(freqSet, H, supportData, brl, minConf=0.7):
#该项集的元素个数
m = len(H[0])
if (len(freqSet) > (m + 1)): #try further merging
#对三元项集列表的元素进行合并成二元项集
Hmp1 = aprioriGen(H, m+1)#create Hm+1 new candidates
print("合并后:",Hmp1)
#对合并后的二元项集筛选出符合条件的关联规则
Hmp1 = calcConf(freqSet, Hmp1, supportData, brl, minConf)
print("筛选后::",Hmp1)
#如果后件元素大于1,继续递归
# if (len(Hmp1) > 1): #need at least two sets to merge
# rulesFromConseq(freqSet, Hmp1, supportData, brl, minConf)
if __name__ == '__main__':
freqSet = frozenset({2,3,5})
H =[frozenset({2}), frozenset({3}), frozenset({5})]
supportData = {frozenset({1}): 0.5, frozenset({3}): 0.75, frozenset({4}): 0.25, frozenset({2}): 0.75, frozenset({5}): 0.75, frozenset({1, 3}): 0.5, frozenset({2, 5}): 0.75,
frozenset({3, 5}): 0.5, frozenset({2, 3}): 0.5, frozenset({1, 5}): 0.25, frozenset({1, 2}): 0.25, frozenset({2, 3, 5}): 0.5}
brl=[]
rulesFromConseq(freqSet, H, supportData, brl, minConf=0.7)
'''合并后: [frozenset({2, 3}), frozenset({2, 5}), frozenset({3, 5})]
筛选后:: ([], [])'''3、总结上面的步骤
#生成关联规则
'''
L:频繁项集列表
supportData:包含频繁项集支持度的字典
minConf=0.7:最小置信度(关联规则用置信度进行量化)
'''
def generateRules(L, supportData, minConf=0.7): #supportData is a dict coming from scanD
#包含置信度的规则列表
bigRuleList = []
#从频繁二项集开始遍历(一个元素的项集没有关联规则)
for i in range(1, len(L)):#only get the sets with two or more items
#遍历所有的二项集
for freqSet in L[i]:
#遍历每个二项集的元素,设置为frozenset集合
H1 = [frozenset([item]) for item in freqSet]
print(H1)
#i>1 三项集
if (i > 1):
rulesFromConseq(freqSet, H1, supportData, bigRuleList, minConf)
else:
#i=1二项集
calcConf(freqSet, H1, supportData, bigRuleList, minConf)
return bigRuleList
if __name__ == '__main__':
L = [[frozenset({5}), frozenset({2}), frozenset({3}), frozenset({1})], [frozenset({2, 3}), frozenset({3, 5}), frozenset({2, 5}), frozenset({1, 3})], [frozenset({2, 3, 5})], []]
supportData = {frozenset({1}): 0.5, frozenset({3}): 0.75, frozenset({4}): 0.25, frozenset({2}): 0.75, frozenset({5}): 0.75, frozenset({1, 3}): 0.5, frozenset({2, 5}): 0.75,
frozenset({3, 5}): 0.5, frozenset({2, 3}): 0.5, frozenset({1, 5}): 0.25, frozenset({1, 2}): 0.25, frozenset({2, 3, 5}): 0.5}
bigRuleList = generateRules(L,supportData)
print("大于最小置信度的关联规则:",bigRuleList)
'''
大于最小置信度的关联规则: [(frozenset({5}), frozenset({2}), 1.0), (frozenset({2}), frozenset({5}), 1.0), (frozenset({1}), frozenset({3}), 1.0)]
'''当然如果要没有顺序就可以改变一下我们的组合候选项集的代码点击打开链接