1 框架解读
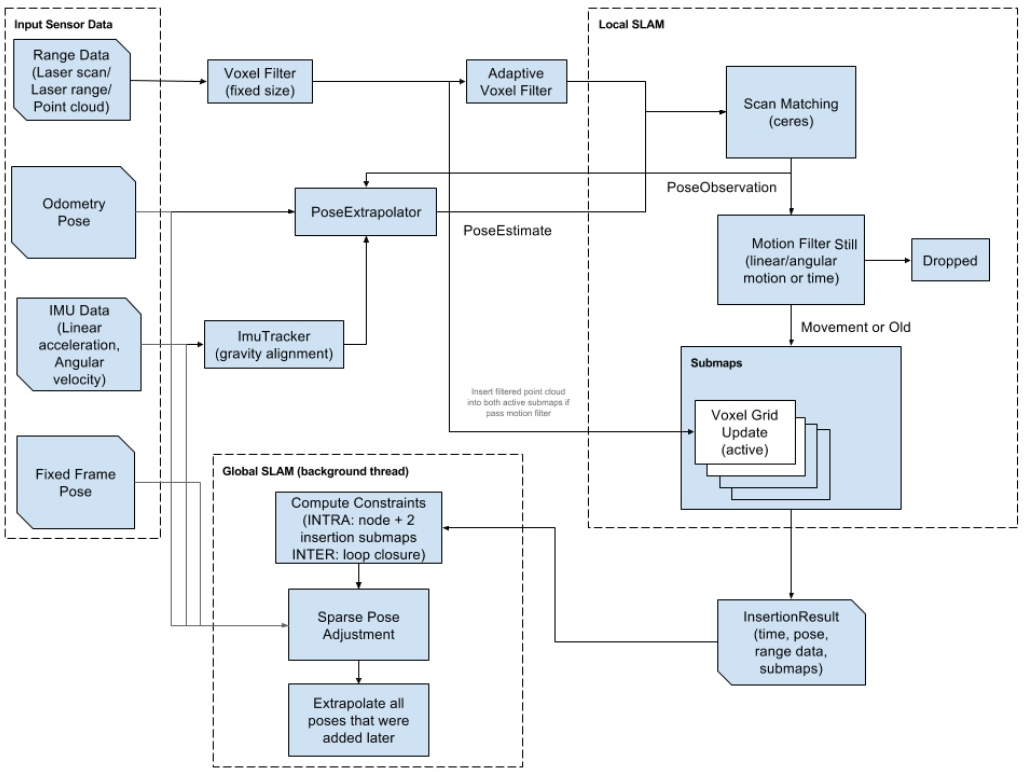
1.1 左侧数据源:
- 激光雷达:两次滤波会根据配置文件选择不同的options,对传感器数据进行两次滤波的作用是减少了一定的数据量
- 里程计、IMU等:为了计算出重力的方向
1.2 Local SLAM(前端):
通过Ceres非线性优化库来求解。Scan Matching通过匹配雷达数据得到的位姿之后,将当前帧的激光(Laser Scan)插入到子图(Submap)中,如果当前帧是没有运动的或者运动缓慢的甚至处于静止状态的,那么可以将这种数据去除(Dropped)。这样一帧一帧的数据处理之后,我们不断更新,就得到了很多的子图。后续当激光数据再次来到时,通过CSM的方法将当前帧的数据插入到子图中。
1.3 Global SLAM(后端):
主要就是回环检测方法。采用分支-定界加速的方法,构建回环,消除子图之间的匹配误差。
2 论文相关工作
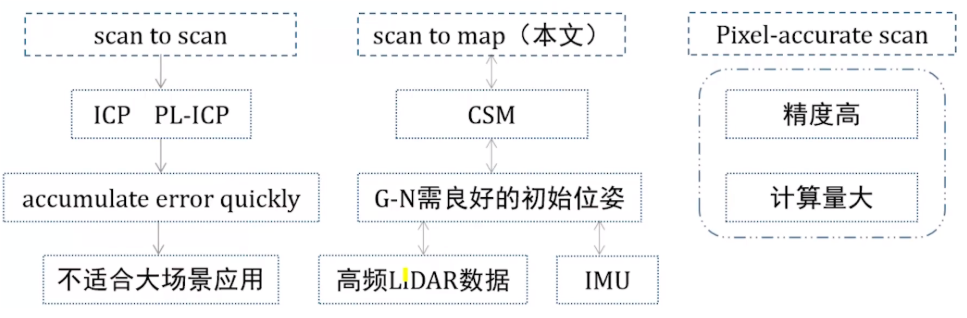
2.1 几种常用的激光数据扫描匹配方法的对比
- scan to scan帧间匹配:ICP或者PL-ICP,这种方法会陷入局部极值的问题,针对大场景计算相对位姿,误差累积会非常明显
- scan to map帧与地图的匹配:这种方法可以限制误差的累积。CSM的相关匹配,其实就是暴力搜索,构建的是势然场模型,不会陷入局部极值。CSM可以理解为在较粗糙的层面下开始的,之后再加一个梯度优化,再进行更精细的搜索,比如使用G-N方法,该方法需要良好的初值,我们可以使用高频的LiDAR数据,或者3D情况下使用IMU来提供。
- pixel-accurate scan精确像素匹配:精度高,但是计算量很庞大
2.1 处理剩余的局部误差累计的方法
-
粒子滤波
基于网格的SLAM来说,随着地图的增大,它很快就变成资源密集型的。
-
图优化
通过节点与边的约束,找到一个最优的配置
3 系统概述
之前的一系列介绍,都旨在引出cartographer算法。主要说明下面的第二点,论文提到的软实时约束。可以理解为并非真正的实时约束,因为它的效率是跟不上的,我们在线跑cartographer的时候会发现它的约束格网是跟不上我们的机器人的行驶速度的。同时,我们更关注的是后端处理的轨迹优化,所以我们会把一些参数设置得更大,实时只是给出了一个初始值位姿。
然而我们在离线跑bag包的时候,我们会发现后端优化也需要一定的过程,比如截图的.lua文件中,表示每90个节点进行一个优化。
第三部分提到了一个分支-定界加速的方法,还有一个预计算的网格。

4 Local 2D SLAM
-
scans:子图的构成其实就是一帧一帧激光数据扫描匹配对齐的迭代过程,每一帧的激光数据转换到子图当中,其实就是一个旋转量R加一个平移t,也就说说T就是通过旋转加平移将激光的框架转换到子图的框架下。
-
submaps:几个连续的激光scan构成了一个子图。这些子图是栅格地图M。其中离散的栅格地图可以理解分辨率,本文采用的是5cm的分辨率。针对2D的格子大小就是5*5大小的格子,然后每一个格子有一个自己对应的概率值,位于最小值Pmin和最大值Pmax的空间中:
- 当栅格的概率值小于Pmin时,表示这个点没有障碍物
- 当栅格的概率值位于Pmin和Pmax之间时,表示一种不确定性
- 当栅格的概率值大于Pmax时,表示这个点是有障碍物的
clamp函数就是一个区间限定函数。这里也提出了预计算网格(precomputed grids)计算原理。当激光点从原点打在一个栅格上时,被击中的栅格,我们进行该格子hit+1的操作,然后激光点和原点进行连线,连线穿过的格子,我们进行该格子miss+1的操作。对于之间没有hit或者miss的格子,我们再为其分配一个概率值。后续再有激光打在栅格上时,我们再重新计算一组hit和miss的值。
-
CSM(最右边部分):在每一帧激光数据插入子图submap前,会使用基于ceres的scan matching对位姿进行优化。这个scan matching负责找到一个扫描位姿,使子图中扫描点scan的概率最大化。这个问题可以转换为一个最小二乘的问题。该公式中的M函数是一个局部构图中概率值的一个平滑版本。这是一个局部的更优化,需要提供一个良好的初值(前文提到,使用高频LiDAR数据,或者3D情况下使用IMU提供)

5 Closing loops
这部分是本文的重点,其中的分支-定界加速和优化问题是cartographer为什么能够达到实时优化的效果。
回环检测的目的:在大场景中通过创建小的子图,来抑制误差的累积。虽然短时间内连续激光数据组成的子图误差累积可以达到很小,但是不同的子图之间仍然可能会有很大的误差,所以仍然需要回环检测来优化我们的位姿。
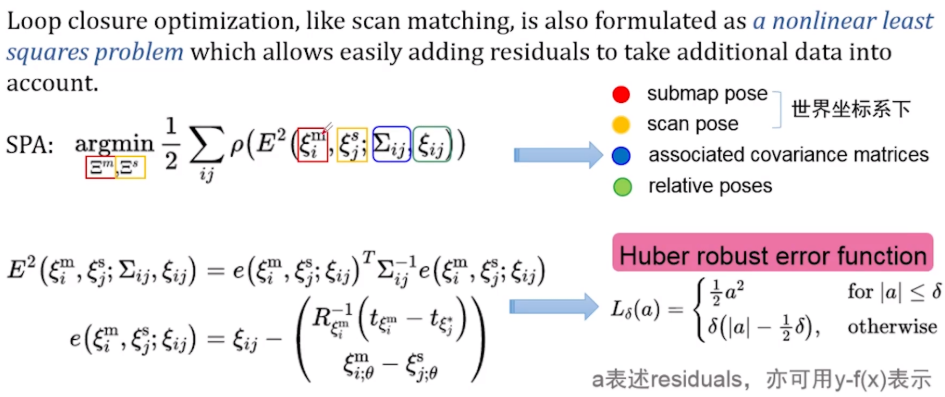
这个优化位姿本质上可以理解为将位姿之间的差值转化为最小二乘问题,这里面提到了一个稀疏姿态调整(Sparse Pose Adjustment, SPA)公式。其中m上角标是子图位姿,s上角标是激光扫描的位姿,第三个是两者之间的协方差,第四个是两者之间的相对位置关系(变换)。
E表示的是他们之间的残差,在这个部分有一个鲁棒性回归的损失函数(Huber robust error function),它相对于均方误差来说,对异常值并不敏感。其中的a可表示观测值和预测值之间的差值(残差),当残差值很小的时候,可以进行平方的操作,当残差值很大的时候,直接加入到系统中会将系统引导到一个错误的方向,所以进行一个线性化的操作,这样避免位系统引入较大的残差项,这在实际应用中主要应用在对称的环境中,减小误差匹配带来的问题。
下面公式中的W是搜索窗口,Mnearest表示的是M将其参数舍入到最近的网格点得到的,其实就是从这个个scan点集周围开始搜索,然后将网格点扩展成为了像素。这个像素的意思就是说,在前端CSM的基础上进行了后端回环检测的进一步匹配。所以将精确度达到一个像素的级别。
左边的符号理解为信度和,是将当前帧插入到子图中,遍历所有位姿得到的最高分。这个值越高,表示越匹配。

我们的目标就是找到这个最高分,但是这样会导致计算量很大,所以本文采用分支-上界法。下面说一下要是想在这个scan点集周围选定一个搜索窗口W寻找最佳的位姿。需要对以下几个参数进行设置:
- 搜索中的角度(angular step)
- 搜索的最远距离(points at the maximum range)
- 搜索的步长(search window)
- 分辨率(width of one pixel)
这部分可以结合算法1来看。从算法1来看,最上面有3层的暴力for循环,这样的话要是想在大场景下实时地应用肯定是不行的。所以加入分支-定界进行加速,右边是给出的一个例子。搜索中间x和y都是7m,角度是30°。W上面加一横线表示搜索空间的集合。
主要思想是将可能性子集表示为树中的节点,其中根节点表示所有可能的解决方案。每个节点的子节点构成其父节点的一个分区,因此它们一起表示相同的可能性集合。通过得分进行判断,为了得到一个具体的算法,我们必须确定选择节点、分支和上界计算的方法。

5.1 节点选择
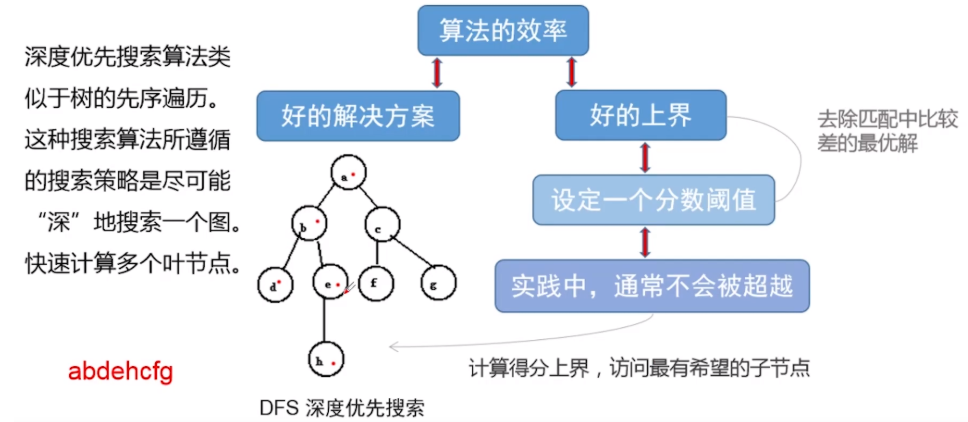
算法的效率取决于两个东西:
-
好的解决方案:
采用深度优先搜索算法。类似于树的先序遍历,这种搜索算法所遵循的搜索策略是尽可能“深”地搜索一个图。快速计算多个叶节点的分值。这一算法在算法3中体现。
-
好的上界:
由于不想把差的匹配添加到回环检测中,所以引入了一个分数阈值,低于这个阈值就对这个部分的最优解不感兴趣,但是在实际过程中这个阈值往往是不会被超越的,所以我们把希望寄托在好的解决方案上。
5.2 分支规则
下面来看一下它是如何进行分支与上界(best_score)的计算。树中的每一个节点都用一个整数的元组c来表示,其中每一个父节点可以分为4个子节点。其中的角度是不变的,x和y都分别加入了新的偏移量。
结合右边的图来看,先假设从最顶层C0开始,计算所有C0层的得分,从大到小依次进行排序。然后再看C1层,计算C1层所有节点得分,再依次从大到小排序。然后重复到底层,计算叶子节点得分,然后将叶子节点中的最高得分记为最高得分(best_score)。将这个最高得到和上一层的非父节点进行相比,如果这个分值比这些非父节点都大,那么就进行剪枝,就这样不断地返回,就得到最高得分(best_score)。

下图中左边是常规的分支定界算法,右边是本文提到的基于DFS的分支定界算法。

6 实验部分
这部分主要是通过跑一些离线数据集,来进行实验的。
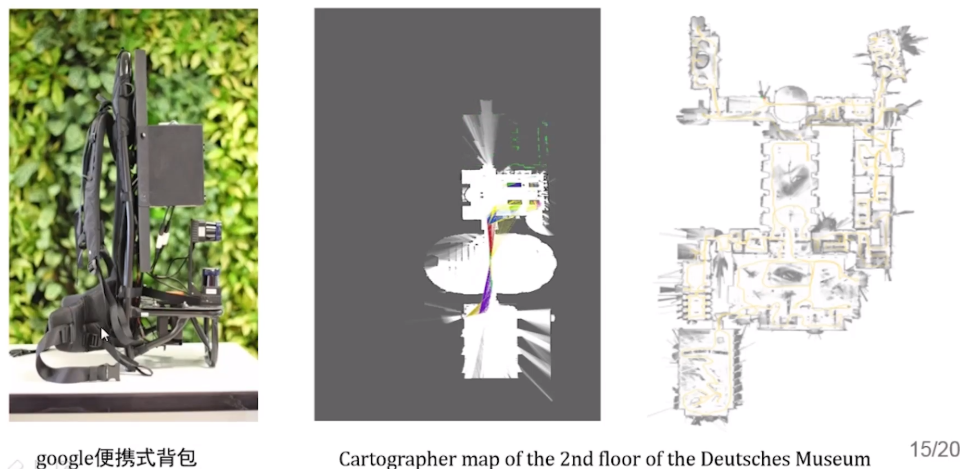
7 结论
- 针对二维的SLAM算法,cartographer除了前端的scan match匹配算法,重点在后端的一个回环检测优化。采用分支定界的方法进行加速,对整个构图进行了优化,证明了高精度实时构图的可能性。