强连通分量是对有向图才有的概念。
联通分量:对于分量中任意两点u,v,必然可以从u走到v,且从v走到u。
强连通分量:极大联通分量(不能再找到更多的点加入联通分量点集)。
联通分量可以将有向图缩点(将所有联通分量缩成一点)变为有向无环图(拓扑图),从而在新的拓扑图上递推(可以线性求最短路,最长路等)。
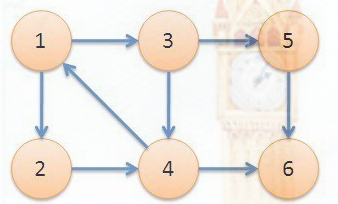
图中,子图{1,2,3,4}为一个强连通分量,因为顶点1,2,3,4两两可达。{5},{6}也分别是两个强连通分量。
tarjin算法求强连通分量
树枝边:DFS时经过的边,即DFS搜索树上的边。
前向边:与DFS方向一致,从某个结点指向其某个子孙的边。
后向边:与DFS方向相反,从某个结点指向其某个祖先的边。(返祖边)
横叉边:从某个结点指向搜索树中的另一子树中的某结点的边。
判断遍历当前点在某个强连通分量中:
1.存在后向边,指向祖先节点。
2.存在横叉边,从横叉边走到祖先节点。
Tarjan算法是基于对图深度优先搜索的算法,每个强连通分量为搜索树中的一棵子树。搜索时,把当前搜索树中未处理的节点加入一个堆栈,回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。 定义DFN(u)为节点u搜索的次序编号(时间戳),Low(u)为u或u的子树能够追溯到的最早的栈中节点的次序号。 由定义可以得出,Low(u)=Min {Low(u), Low(v) } (u,v)为树枝边,u为v的父节点 . Low(u)=Min {Low(u), DFN(v) }DFN(v),(u,v)为指向栈中节点的后向边(指向栈中结点的横叉边) } 当结点u搜索结束后,若DFN(u)=Low(u)时,则以u为根的搜索子树上所有还在栈中的节点是一个强连通分量。
注意求完tarjin之后,建立新图 过程:
for(int i=1;i<=n;i++) for(i 的所有邻点j) if(i和j不在同一联通分量中) 加一条 id[i]到id[j]的新边
建立的新图按for(int i=scc_cnt;i>=1;i--)的顺序即为拓扑序。
简单说明:在tarjin算法中对于找到每一个强联通分量,当处理他们的时候,此时已经遍历完了子树的所有边,意味着此时强联通分量最高点已经没有出边。所有倒叙即为新图的拓扑序。
注意这点很重要(可以简化求拓扑序的过程)。
代码:
1 void tarjin(int u) 2 { 3 stk.push(u);//加入栈中 4 low[u]=dfn[u]=++times;//时间戳 5 is_stk[u]=true;//该元素已经进栈 6 for(int i=h[u];i!=-1;i=ne[i]) 7 { 8 int j=e[i]; 9 if(!dfn[j])//子树未遍历就遍历 10 { 11 tarjin(j); 12 low[u]=min(low[u],low[j]); 13 } 14 else if(is_stk[j]) low[u]=min(low[u],low[j]);//遍历到更早的点 15 } 16 if(low[u]==dfn[u])//此时u是一个强联通分量高度最高的点 17 { 18 int y; 19 ++scc_cnt;//强联通分量标记 20 while(y!=u) 21 { 22 y=stk.top(); 23 stk.pop(); 24 is_stk[y]=false;//标记元素出栈 25 siz[scc_cnt]++;//记录每个强连通分量大小 26 id[y]=scc_cnt;//标记原图每个点属于哪个强连通分量 27 } 28 } 29 }
建新图代码:
1 unordered_set<ll>S; 2 for(int i=1;i<=n;i++) 3 for(int j=h[i];j!=-1;j=ne[j]) 4 { 5 int k=e[j]; 6 int a=id[i],b=id[k]; 7 ll Hash=a*1000000ll+b;//如果题目要求不能建重边需要对边判重。 8 if(a!=b&&S.count(Hash)) 9 { 10 add(hs,a,b); 11 S.insert(Hash); 12 } 13 }