影评推荐系统

1、创建django

创建文件夹保存文件：

mkdir 文件夹

cd 文件夹

django-admin startproject  项目名称

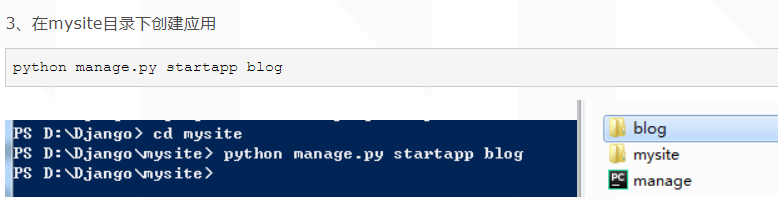
在项目下创建应用

影评数据采用爬虫知识，使用scrapy库从bing搜索引擎采取和抽取

1、爬取数据

必应（英语：Bing，台港称Bing）是一款由微软公司推出的网络搜索引擎。

简短几十行代码之后你已经能够开始抓取一部电影的全部短评和评分了。在这之前，记得在settings里加一个DOWNLOAD_DELAY = 2，不然的话爬不到一半就会被豆瓣给禁了。

 我们的应用(spider文件夹)使用两个蜘蛛：

一只从影评URL抽取数据(movice_link_results.py)

另外一只生成所有链接到初始影评URL的网页连接图(recursive_link_results.py)

将爬取到的数据保存到Django model PageItem中

线性回归

线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。其表达形式为y = w'x+e，e为误差服从均值为0的正态分布。
回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。
其实，说白了，就是用一条直线去拟合一大堆数据，最后把系数w和截距b算出来，直线也就算出来了， 就可以拿去做预测了。
sklearn中线性回归使用最小二乘法实现，使用起来非常简单。
线性回归是回归问题，score使用R2系数做为评价标准。

import sklearn.linear_model as sk_linear
model = sk_linear.LinearRegression(fit_intercept=True,normalize=False,copy_X=True,n_jobs=1)
model.fit(X_train,y_train)
acc=model.score(X_test,y_test) #返回预测的确定系数R2
print('线性回归:')
print('截距:',model.intercept_) #输出截距
print('系数:',model.coef_) #输出系数
print('线性回归模型评价:',acc)

参数说明：
fit_intercept：是否计算截距。False-模型没有截距
normalize： 当fit_intercept设置为False时，该参数将被忽略。 如果为真，则回归前的回归系数X将通过减去平均值并除以l2-范数而归一化。
copy_X：是否对X数组进行复制,默认为True
n_jobs：指定线程数

打印结果：

线性回归:
截距: -0.379953866745
系数: [-0.02744885  0.01662843  0.17780211  0.65838886]
线性回归模型评价: 0.913431360638

https://www.jianshu.com/p/731610dca805

决定系数R^2
决定系数（coefficient ofdetermination），有的教材上翻译为判定系数，也称为拟合优度。

决定系数反应了y的波动有多少百分比能被x的波动所描述，即表征依变数Y的变异中有多少百分比,可由控制的自变数X来解释。

意义：拟合优度越大，说明x对y的解释程度越高。自变量对因变量的解释程度越高，自变量引起的变动占总变动的百分比高。观察点在回归直线附近越密集。
所以我们用到了一种方法叫 coefficient of determination (决定系数) 来判断 回归方程 拟合的程度
-------------------------------------------------------------------------------------
表达式：R2=SSR/SST=1-SSE/SST

其中：SST=SSR+SSE，SST(total sum of squares)为总平方和，SSR(regression sum of squares)为回归平方和，SSE(error sum of squares) 为残差平方和。
--------------------- 

统计学——线性回归决定系数R2

作为博客里面的模型图

Python统计分析库statsmodels的OLS

多元线性回归分析

基于Python的博客设计与开发毕业设计