Largest Rectangle in a Histogram

题：

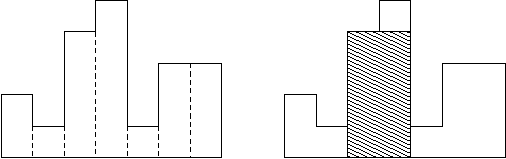
如图所示，在一条水平线上有n个宽为1的矩形，求包含于这些矩形的最大子矩形面积（图中的阴影部分的面积即所求答案）。

输入格式： 有多组测试数据，每组数据占一行。输入零时读入结束。

每行开头为一个数字n（1<=n<=100000）,接下来在同一行给出n个数字h1h2...hn（0<=hi<=1000000000）表示每个矩形的高度。

输出格式： 对于每组数据，输出最大子矩阵面积，一组数据输出一行。





思路：维护一个单调递增的栈 栈里存的是矩形的高和宽 维护子矩形的高单调递增

　　　若现在的矩形（宽度为一） 的高度大于栈顶矩形的高直接压栈

           否则就要把前面比它大的都弹出 同时计算出从这个矩形开始向左可以扩展的每个矩形的面积 更新答案

          觉得这道题很好qwq

code

#include<iostream>
#include<cstdio>
#include<cstring>
#define ll long long
#define go(i,a,b) for(register int i=a;i<=b;i++)
using namespace std;
ll read()
{
  ll x=0,y=1; char c; c=getchar();
  while(c<'0'||c>'9') {if(c=='-') y=-1;c=getchar();}
  while(c>='0'&&c<='9') {x=(x<<3)+(x<<1)+c-'0';c=getchar();}
  return x*y;
}
struct node
{
  ll h,w;
}rec[100010];
ll ans,h,top,n;
int main()
{
  while(1)
    {
      n=read();if(!n) break ;
      n+=1;ans=0;top=0;
      go(k,1,n)
    　　{
     　　 if(k!=n) h=read(); else h=0;
     　　 if(h>=rec[top].h) rec[++top]=(node){h,1};
      　　else
      　　  {
      　　    ll w=0;
      　　    while(h<rec[top].h)
       　　 　　{
        　　 　　 w+=rec[top].w;
        　　 　　 ans=max(ans,(ll)w*rec[top].h);
        　　 　　 top--;
     　　  　　 }
      　　    rec[++top]=(node){h,w+1};
       　　 }
 　　   }
   　　   printf("%lld
",ans);
  }
  return 0;
}