图 基础

基本概念

连通：如果图中结点U、V之间存在一条从U通过若干条边、点到达V的通路，则称U、V是连通的

完全图：每对顶点之间有唯一的一条边相连或想通。无向图共有：n*(n-1)/2条边，有向图共有：n*(n-1)条边

子图: 边的子集和相关联的点集

强联通分量：有向图中任意两点都连通的最大子图

补图：对于(u,v), 若邻接则改为非邻接, 若非邻接则改为邻接, 得到的图为原图的补图

团：完全子图

割点：如果从图中删去某点和与该点相关联的边后，图不再连通，那么这个点叫做割点，也称顶点或关节点

割边：如果从图中删去某条边后，图不再连通，那么这条边叫做割边或桥

---

割点与割边

• 若生成树的根有两棵或两棵以上的子树，则此根顶点必为割点。
• 若生成树中某个非叶子顶点v，它的子树中的任一结点均没有指向v的祖先的回边，则v为割点。

(ps:我们定义dfn[i]为节点i搜索的次序编号(时间戳)，low[i]为i或i的子树能够追溯到的最早的栈中节点的次序号。)

实现：当low[j]<dfn[i](j是i的儿子)时，说明j或者j的子孙中存在指向i祖先的回边。反之，若对于某个顶点v，存在孩子结点w，且low[w]>=dfn[v],表明w及其子孙均无指向v的祖先的回边，则该顶点v必为割点。

• 在任何DFS树中，当且仅当不存在回边连通w的子孙与w的祖先时，树边v-w是一座桥。

实现：与割点类似的，我们定义low[]和dfn[]。父子边e=u→v ，当且仅当low[v] > dfn[u]的时候，e是割边。

强连通分量Tarjan算法

Tarjan算法是基于对图深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树。dfs时，把当前搜索树中未处理的节点加入一个堆栈，回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。

当dfn(u)=low(u)时，以u为根的搜索子树上的所有节点构成一个强连通分量。

例题：洛谷2341受欢迎的牛

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int M=60000,N=20000;
struct node
{
    int to;         //这条边到达的点 
    int next;       //下一条边的编号 
}a[M];              //链式前向星 
int b[N];           //链式前向星 
int n,m;            //n:奶牛数;m:喜欢关系数
int bnum=0;         //边数 
int dfn[N],low[N];  //dfn[i]:表示结点i是第dfn[i]个被访问到的结点
                    //low[i]用来记录i及i的子孙相连的辈分最高的祖先的访问时间戳
int top,st[N];      //top:栈的指针;st:栈 
int tot;            //遍历序数 
bool f[N];          //是否考虑过 
int cnum;           //标记不同的强连通分量 
int be[N];          //被标记到不同强连通分量 
int size[N];        //size[i] 被标记为i的强连通分量的个数 
bool w[N];          //w[i]:被标记为i的强连通分量是否有出度 1:有;0:没有; 
int read()          //读入优化 
{
    int sum=0;
    char ch;
    ch=getchar();
    while(ch>'9'||ch<'0') ch=getchar();
    while(ch>='0'&&ch<='9') sum=sum*10+ch-'0',ch=getchar();
//    cout<<"read: "<<sum<<endl;
    return sum;
}
void lian(int to,int from)    //链式前向星   to,from!!!!!!! 
{
    a[++bnum].next=b[from];  //cout<<from<<" "<<to<<"  !"<<endl;
    a[bnum].to=to;
    b[from]=bnum;
}
void dfs(int x)
{
    dfn[x]=low[x]=++tot;             //初始 dfn low 值 
    st[++top]=x;                     //入栈 
    f[x]=1;                         
    for(int i=b[x];i;i=a[i].next)
    {
        if(!dfn[a[i].to])
        {
            dfs(a[i].to);
            low[x]=min(low[x],low[a[i].to]);     //更新 low 值 
        }
        else if(f[a[i].to])          //如果走过   是回边 
        {
            low[x]=min(low[x],low[a[i].to]);
        }
    }
    if(low[x]==dfn[x])
    {
        cnum++;         //标记强连通分量 
        int now;      
        while(now!=x)
        {
            now=st[top--];
            be[now]=cnum;
            size[cnum]++; 
        } 
        /*for(int i=top+1;i<=top+size[cnum];i++)         //是否有出度 
        {
            if(!w[cnum]) 
            for(int j=b[i];j;j=a[j].next)
            {
                if(be[a[j].to]!=cnum) 
                {w[cnum]=1;break;}           //有出度 不是强连通分量 
            }
        }*/
    }
}
int main()
{
    n=read();m=read();             //read:读入优化 
    for(int i=1;i<=m;i++)
    {
        lian(read(),read());
    }
    for(int i=1;i<=n;i++)        //dfs：寻找强连通分量 
    {
        if(!dfn[i]) dfs(i);
    }
    for(int i=1;i<=n;i++)
    {
        if(w[be[i]]) continue;
        for(int j=b[i];j;j=a[j].next)
        {
            if(be[i]!=be[a[j].to])
            {
                w[be[i]]=1;
                break;
            }
        }
    } 
    int ans=0;   //最终答案 
    for(int i=1;i<=cnum;i++)
    {
        if(!w[i])
        {
            if(ans)
            {
                putchar('0');
                return 0;
            }
        else ans=size[i];
        }
    }
    printf("%d",ans);
    return 0;
} 

最短路问题

• Dijkstra：单源最短路，不含负权
• bellman-ford：单源最短路，可含负权，但不能有负权回路：
• SPFA：Bellman-ford的队列优化
• floyd-warshall：每两对点的最短路，可含负权

#include<iostream>
#include<queue>
#include<cstdio>
using namespace std;
int ans[10010];
bool f[10010];
struct node
{
    int to;
    int data;
    int next;
}a[1000010];
struct cmp
{
    bool operator()(int a,int b)
    {
        return ans[a]<ans[b];
    }
};
int b[10010];
int tot;
priority_queue<int,vector<int>,cmp>h;
void lian(int from,int to,int sum)
{
    a[++tot].next=b[from];
    a[tot].to=to;
    a[tot].data=sum;
    b[from]=tot;
}
int main()
{
    int n,m,s;
    cin>>n>>m>>s;
    for(int i=1;i<=n;i++) ans[i]=2147483647;
    for(int i=1;i<=m;i++)
    {
        int a,b,c;
        cin>>a>>b>>c;
        lian(a,b,c);
    }
    ans[s]=0;
    h.push(s);
    f[s]=1;
    int num=0;
    for(int k=1;k<=n;k++)
    {
        int num;
        num=h.top();
        f[num]=0;
        h.pop();
        if(num)
        {
            f[num]=1;
            for(int i=b[num];i;i=a[i].next)
            {
                ans[a[i].to]=min(ans[a[i].to],ans[num]+a[i].data);
                h.push(a[i].to); 
            }
        }
    }
    for(int i=1;i<=n;i++) cout<<ans[i]<<" ";
    return 0;
} 

#include<iostream>
#include<cstdio>
using namespace std;
const int M=21000;
struct node
{
    int to;
    int data;
    int next;
    int from;
}a[1000010];
int b[1010];
int ans[1010];
int tot=0;
void lian(int from,int to,int sum)
{
    a[++tot].next=b[from];
    a[tot].to=to;
    a[tot].data=sum;
    a[tot].from=from;
    b[from]=tot;
 } 
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++) ans[i]=M;
    for(int i=1;i<=m;i++)
    {
        int a,b,c;
        cin>>a>>b>>c;
        lian(a,b,c);
        if(a==1) ans[b]=c;
    }
    for(int k=1;k<=n-1;k++)
    {
        for(int i=1;i<=m;i++)
        {
            if(ans[a[i].from]*a[i].data<ans[a[i].to])
            {
                ans[a[i].to]=ans[a[i].from]*a[i].data;
            }
        }
    }
    cout<<ans[n];
    return 0;
} 

#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;
const int M=21000000;
struct node
{
    int to;
    int data;
    int next;
    int from;
}a[1000010];
int b[1010];
int ans[10010];
bool f[10010];
int tot=0;
queue<int>h;
void lian(int from,int to,int sum)
{
    a[++tot].next=b[from];
    a[tot].to=to;
    a[tot].data=sum;
    a[tot].from=from;
    b[from]=tot;
 } 
int main()
{
    int n,m,s;
    cin>>n>>m>>s;
    for(int i=1;i<=n;i++) ans[i]=M;
    for(int i=1;i<=m;i++)
    {
        int a,b,c;
        cin>>a>>b>>c;
        lian(a,b,c);
    }
    h.push(s);f[s]=1;
    ans[s]=0;
    while(!h.empty())
    {
        int q=h.front();h.pop();
        f[q]=0;
        for(int i=b[q];i;i=a[i].next)
        {
            if(ans[q]+a[i].data<ans[a[i].to])
            {
                if(!f[a[i].to])  
                {
                    h.push(a[i].to);
                    f[a[i].to]=1;
                }
                ans[a[i].to]=ans[a[i].from]+a[i].data;
               }
        }
    }
    for(int i=1;i<=n;i++) cout<<ans[i]<<" ";
    return 0;
} 

最小生成树

• Prim算法（加点法）
• Kruskal算法（加边法）

//https://www.luogu.org/problemnew/show/P3366 
#include<iostream>
#include<cstdio>
using namespace std;
int n,m;
int data[5010][5010];    //data[i][j]:i到j的路长度
int dis[5100]; 
bool f[5100];         //是否为生成树中的点 
int read()           
{
    int sum=0;
    char ch;
    ch=getchar();
    while(ch>'9'||ch<'0') ch=getchar();
    while(ch>='0'&&ch<='9') sum=sum*10+ch-'0',ch=getchar();
    return sum;
}
int main()
{
    n=read();m=read();
    for(int i=1;i<=n;i++) dis[i]=210000;
    for(int i=1;i<=m;i++)
    {
        int a,b,c;
        a=read();b=read();c=read();
        if(c<data[a][b]||!data[a][b]) data[a][b]=data[b][a]=c;
        //if(a==1) dis[b]=c;
    }
    dis[1]=0;
    int ans=0; 
    for(int k=1;k<=n;k++)
    {
        int num1=210000,num2=0;
        for(int i=1;i<=n;i++)
        {
            if(dis[i]<num1&&!f[i])
            {
                num1=dis[i];
                num2=i;
            }
        }
        if(num2)
        {
            ans+=dis[num2];
            f[num2]=1;
            for(int i=1;i<=n;i++)
            {
                if(data[num2][i]!=0&&data[num2][i]<dis[i]&&!f[i])
                {
                    dis[i]=data[num2][i];
                  }
            }
        }
    }
    for(int i=1;i<=n;i++)
    if(!f[i]) {cout<<"orz";return 0;}
    cout<<ans;
    return 0; 
} 

//太简单了我不写了qwq

差分约束系统

 

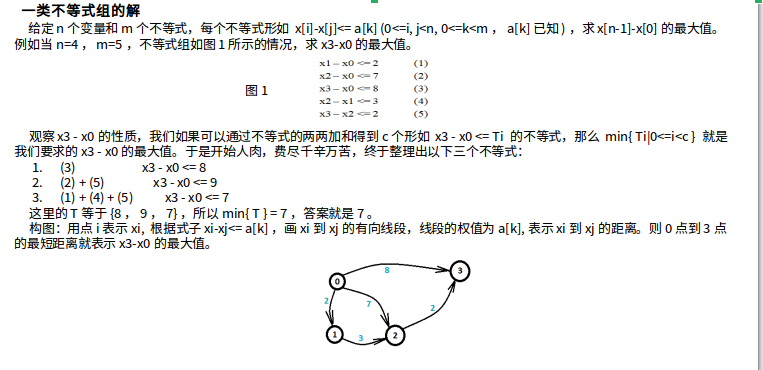
只想补充讲一点啦（第一张图片中的图中）：0-3的每一条路的权值其实都是由经过路径所代表的不等式综合起来的最大值 由于要满足每个不等式，所以求这些最大值的最小值

例题：[SCOI2011]糖果

#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;
inline int read()
{
    char ch;int sum=0;
    ch=getchar();
    while(ch<'0'||ch>'9') ch=getchar();
    while(ch>='0'&&ch<='9') {sum=sum*10+ch-'0';ch=getchar();};
    return sum;
}
int n,m;
int a[100010],num;
struct node
{
    int to,data,next;
}b[200010];
void lian(int from,int to,int sum)
{
    b[++num].next=a[from];
    b[num].to=to;
    b[num].data=sum;
    a[from]=num;
}
queue<int> h;
int dis[100010];
bool f[100010];         //是否在队列中 
int nn[100010];
bool SPFA()
{
    dis[0]=0;        
    f[0]=1;
    h.push(0); 
    while(!h.empty())
    {
        int x=h.front();
        h.pop();
        f[x]=0;
        for(int i=a[x];i;i=b[i].next)
        {
            //cout<<"!";
            if(b[i].data+dis[x]>dis[b[i].to])
            {
                dis[b[i].to]=b[i].data+dis[x];
                if(!f[b[i].to]) 
                {
                    if(++nn[b[i].to]>n) {cout<<b[i].to<<endl;return 0;}
                    h.push(b[i].to);
                    f[b[i].to]=1; 
                }
            }
        }
    }
    return 1;
}
int main()
{
    n=read();m=read();
    for(int i=1;i<=m;i++) 
    {
        int x,a,b;
        x=read();a=read();b=read();
        if(x==1) 
        {
            lian(a,b,0);
            lian(b,a,0);
        }
        if(x==2)
        {
            if(a==b) {cout<<"-1";return 0;}
            lian(a,b,1);
        }
        if(x==3) lian(b,a,0);
        if(x==4)
        {
            if(a==b) {cout<<"-1";return 0;}
            lian(b,a,1);
        }
        if(x==5) lian(a,b,0);
    }
    for(int i=1;i<=n;i++)
    lian(0,i,1);                    ////每个小朋友都至少有一个糖果!!!!
    if(!SPFA()) {cout<<"-1";return 0;};
long long ans=0;
    for(int i=1;i<=n;i++) ans+=dis[i];
    cout<<ans;
    return 0;
}

LCA

在这里qwq

负环

// luogu-judger-enable-o2
#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
using namespace std;
int read()
{
    int ans=0,x=1;char c;
    c=getchar();
    while(c<'0'||c>'9') {if(c=='-') x=-1;c=getchar();}
    while(c>='0'&&c<='9') {ans=ans*10+c-'0';c=getchar();}
    return ans*x;
}
const int N=100010;

struct node         //链式前向星 
{
    int to,data,next;
}a[N]; 
int b[N],num;
void lian(int u,int v,int w)
{
    a[++num].next=b[u];
    a[num].to=v;
    a[num].data=w;
    b[u]=num;
}

int n,m;
bool vis[N];
int dis[N],times[N];

bool spfa()
{
    for(int i=1;i<=n;i++) {vis[i]=0;dis[i]=2100000000;times[i]=0;}
    queue<int>h;
    h.push(1);
    vis[1]=1;
    dis[1]=0;
    while(!h.empty())
    {
        int u=h.front();h.pop();vis[u]=0;
        //cout<<u<<"  !"<<endl;
        if(times[u]>=n) return 1;
        for(int i=b[u];i;i=a[i].next)
        {
            int v=a[i].to;
            if(dis[v]>dis[u]+a[i].data)
            {
                dis[v]=dis[u]+a[i].data;
                if(!vis[v])
                {
                    h.push(v);
                    vis[v]=1;
                    times[v]++;
                    if(times[v]>=n) return 1;
                }
            }
        }
    }
    return 0;
}
int main()
{
    int t=read();
    while(t--) 
    {
        n=read(),m=read();
        num=0;
        memset(b,0,sizeof(b));
        for(int i=1;i<=m;i++)
        {
            int x=read(),y=read(),z=read();
            lian(x,y,z);
            if(z>=0) lian(y,x,z);
        }
        puts(spfa()?"YE5":"N0");
    }
    return 0;
}