论文阅读笔记五十四：Gradient Harmonized Single-stage Detector（CVPR2019）

论文原址：https://arxiv.org/pdf/1811.05181.pdf

github:https://github.com/libuyu/GHM_Detection

摘要

       尽管单阶段的检测器速度较快，但在训练时存在以下几点不足，正负样本之间的巨大差距，同样，easy,hard样本的巨大差距。本文从梯度角度出发，指出了上面两个不足带来的影响。然后，作者进一步提出了梯度协调机制(GHM)用于避开上面的不足。GHM的思想可以嵌入到用于分类的交叉熵损失或者用于回归的Smooth-L1损失中，最后，本文修改过的损失函数GHM-C与GHM-R用于平衡anchor分类及回归二者的梯度。

介绍

      单阶段检测网络十分高效，但是与二阶段检测在准确率上仍存在一定的差距。单阶段检测训练过程最具挑战的难点在于easy 与hard 样本之间的不平衡以及正负样本的不平衡问题。大量的简单背景样本会占据训练的主导地位。而在两阶段网络中不存在样本不平衡的问题，这是因为在两阶段网络中存在这proposal-driven的机制。后来，出现了基于OHEM的样本挖掘技术，但这种方法舍弃了大部分样本，训练也不是很高效，后来Focal Loss通过修改损失函数来调整不平衡问题。但是Focal loss引入了两个超参数，需要进行大量的实验进行调试，同时，Focal loss是一种静态损失，对数据集的分布不敏感，而在训练过程中，数据集的分布是会发生变化的。

      本文指出类别不平衡主要难点在于不平衡，而不平衡可以归结为，梯度正则分布的不平衡。如果一个负样本很容易被分类，则该样本为easy example同时模型从中得到的信息量较少，比如，通过这个样本，只产生了一点梯度信息。模型应该关注这个被分错的样本。从整体上来看，负样本易于被分类多为easy examples，而hard examples多为正样本。因此，两种不平衡可以归结为属性上的不平衡。

      上面两种类型的不平衡(hard/easy , positive/negative)可以由gradient norm的分布表示。带有梯度正则的样本密度，被称为梯度密度，如下图左侧所示，由于存在大量的简单负样本，小梯度正则的样本的密度很大。虽然一个简单样本对整体的梯度贡献很小，但大量的简单样本作用后会占据训练的主导，使训练过程并不是很高效。

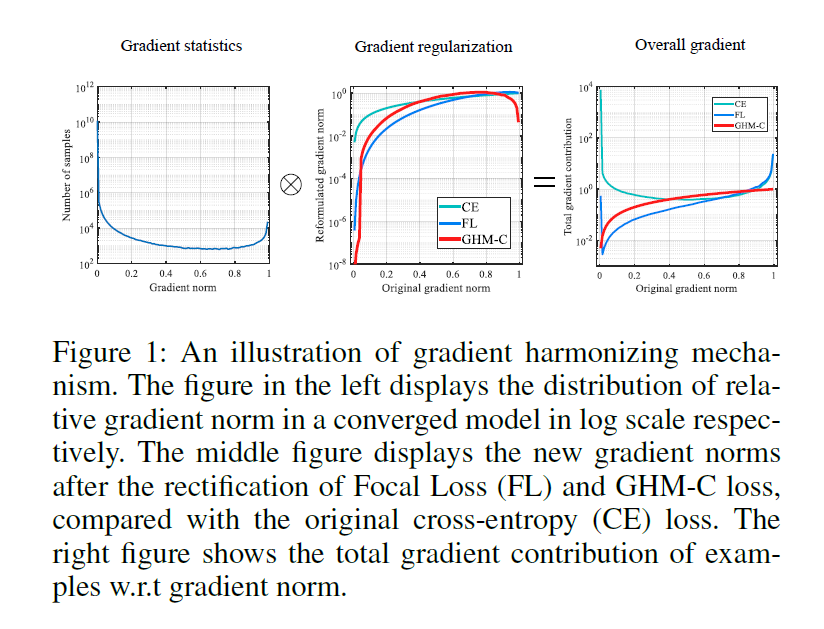
      本文发现，带有较大梯度正则(very hard examples)的样本密度比medium examples略多一点。本文将这些very hard examples看作为异常点，因为即使模型收敛，但这些点仍稳定存在。同时，异常点的梯度与其他正常点的差异较大，进而会影响模型的稳定性。

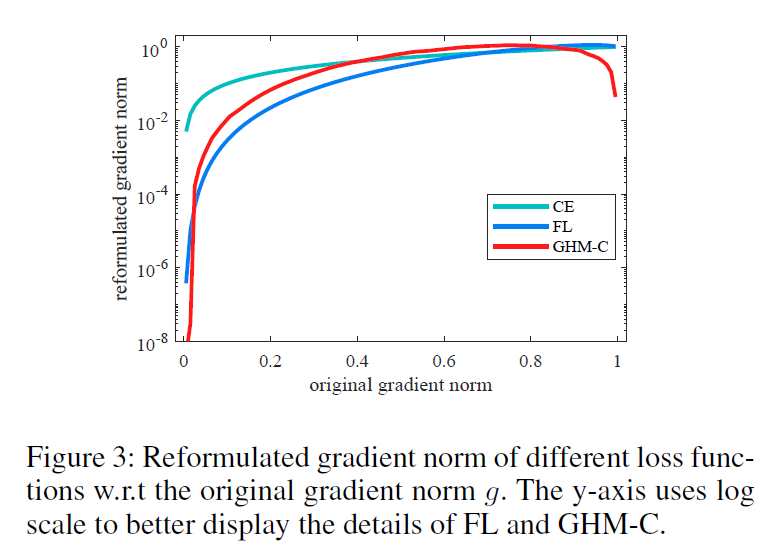
      本文分析了梯度正则分布后就提出了gradient harmonizing mechanism(GHM)算法用于对单阶段检测进行高效的训练，用于协调不同样本之间的梯度分布。GHM首先对具有相似属性（如梯度密度）样本的数量进行统计，然后根据密度在每个样本的梯度上附加一个调节参数。相比CE，FL，GHM的效果如上图右侧所示，带GHM的训练过程，由大量简单样本计算得到的梯度的权重被大幅度减少，同时异常点的权重也被相应的削弱。

      通过修改损失函数可以对梯度进行修正，本文将GHM嵌入到分类损失中，得到GHM-C损失，该损失不需要参数调节。由于梯度密度是由minibatch中样本分布决定的统计变量，在每一轮batch中，GHM-C是可以更具数据分布变化进行调整进而更新模型的动态损失。为了表明GHM的一般性，在边界框的回归分支中应用GHM，代表GHM-R损失。

Gradient Harmonizing Mechanism

      问题描述：本文的关注点在于单阶段检测中样本类别的极度不平衡问题。对于一个候选框，模型预测出的概率为p [0,1],P*代表对于特定类别的ground truth 标签取值0或1，其二分类的交叉熵损失如下所示

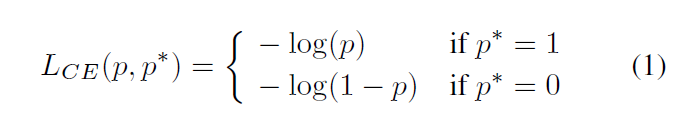
      而后，令x作为模型的输出因此，p=sigmoid(x)，对其求导如下，

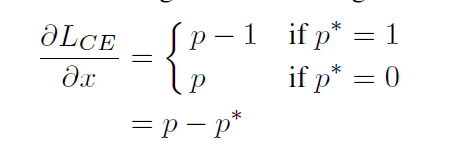
      定义了g等式如下所示，g与Lce对x的偏导值的正则相等，g代表一个样本的属性以及该样本对整体梯度的作用，本文将g称为梯度正则。

      下图展示了一个收敛的单阶段检测模型的g的分布。由于简单负样本的体量较大，使用log坐标来表示样本的比例，进而展示不同属性样本变化细节。从图中可以看出简单样本的数量非常大，对整体的梯度造成了一定的影响。另外，稳定的模型仍然无法处理very hard examples，其数量要比medium的样本的数量还要多一些。这些样本可以被看作是异常点，其梯度方向与大部分其他样本的梯度方向差异很大。如果模型对这些异常点的学习较好，则其他大部分样本的准确率相对就会低一些。

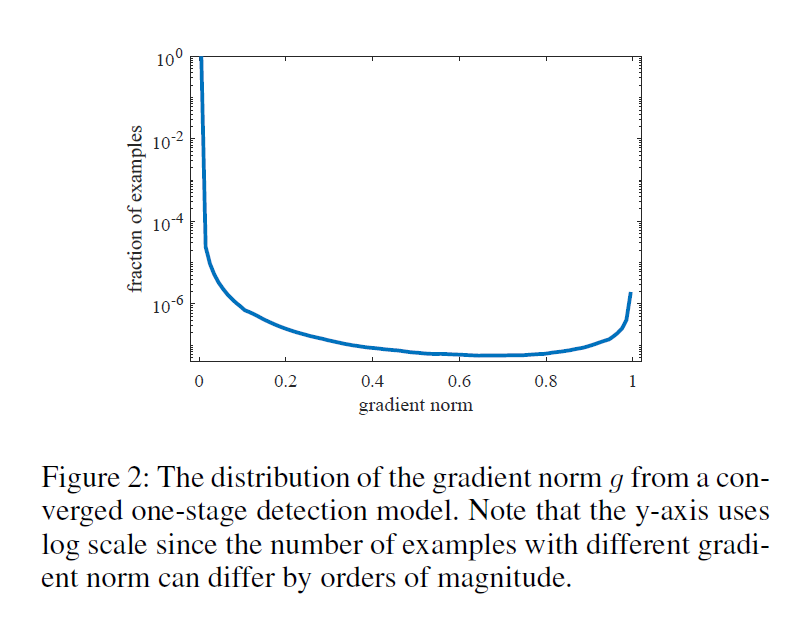
      梯度密度：为了解决梯度正则分布中的不平衡问题，引入了一个针对梯度密度的协调方法，训练样本的梯度密度函数如下所示

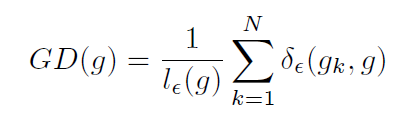
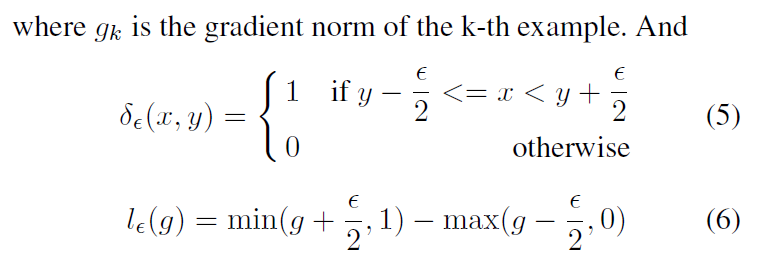
       g的梯度密度表示位于以g为长度为的样本的数量，同时，基于区域的有效长度来对其进行正则化处理。梯度协调参数的定义如下所示，N表示样本数量的总数，

      对上式进行变换，得到，为一个正则项，代表与第i个样本其相邻梯度值的样本数所占的比例。如果样本服从均匀分布，则GD(gi)=N，对于任意gi及每个样本，其参数值都为1，表示不需要进行改变，否则，通过这个正则项，可以相对降低大密度样本的权重。

      GHM-C Loss:损失函数如下，

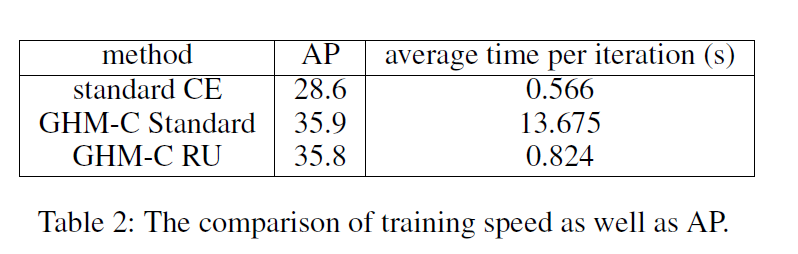
      如下图所示，大量的简单样本的权重被衰减，同时异常值的权重也被降低。同时，其梯度密度在每一轮迭代中会发生变化，样本的权重并不是固定的，因此GHM-C损失的动态属性可以使训练更加高效鲁棒。

      Unit Region Approximation：复杂度分析：常规计算所有样本梯度值的算法复杂度为O(N^2)，即使使用并行计算，每个计算节点仍有N的计算量。比较好的算法首先会以O(NlogN)的复杂度通过梯度正则对样本进行排序，然后使用一个队列来扫描样本，以O(N)的方式得到密度。由于单阶段检测中的N为1e5或者1e6，其梯度计算量仍很大，基于排序的算法比并行计算提升的幅度有限。本文提出了近似的获得样本梯度密度的方法。

      Unit Region：将g的空间划以间隔分为独立的单元区域  ，因此有个单元区域。rj代表索引为j的区域，，

令Rj代表落入rj区域的样本数量。定义用于获得g所在单元区域的索引。

     定义近似梯度密度函数，

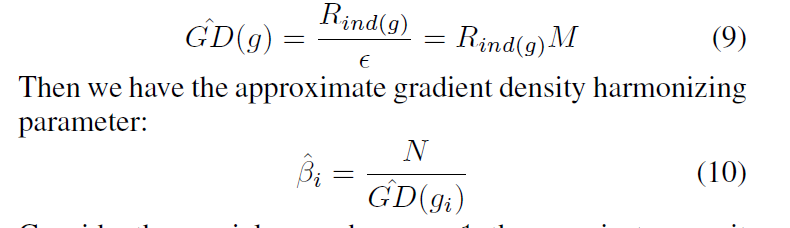
     假设参数为1，只有一个单元，所有的样本都在此区域，其梯度不会发生变化。其损失函数如下所示。

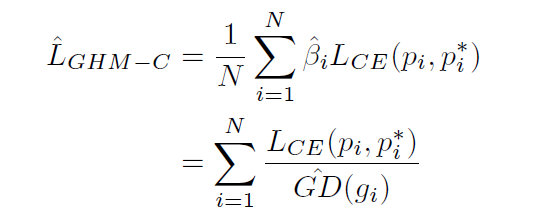
     根据等式9，可以返现，落在相同区域的样本的梯度密度值是相同的，可以利用直方图统计，所有样本梯度密度的计算的时间复杂度为O(MN)，同时，可以应用并行计算，因此每个计算单元复杂度为M,e而M的值相对较小，因此损失的计算比较高效。

      EMA：基于Mini-batch统计的方法存在一个问题：当一个mini-batch中存在大量的异常点时，统计结果为噪声，而且使训练变得不稳定。Exponential moving average(EMA)是解决此问题的常用方法，比如带动量的SGD及BN处理。由于梯度密度的近似计算中的样本来自于单元区域，因此可以在每个单元区域应用EMA，进而得到更多稳定的梯度密度。等式如下

      GHM-R Loss:观察偏移参数量,由模型预测出的及目标偏移如下所示，

      回归损失通常基于smooth L1损失函数，

      当所有|d|>的样本，具有相同的梯度正则，，如果依赖于梯度密度，则无法区分不同属性的样本，相比直接使用|d|作为区分不同属性的评价标准，而|d|的理论值可以达到无限，单元区域近似无法应用到上面，为了简化GHM在回归损失上的应用，首先更改SL1的损失如下，

      当d很小时，近似为一个方差函数(L2 loss)，当d很大时近似一个线性损失（L1 loss），称该损失为Authentic Smooth L1损失，就有很好的平滑性，其偏导存在且连续。ASL1的偏导如下，梯度值的范围[0,1)，单元区域中梯度的计算和CE损失的计算一样较为方便。令u=0.02

         定义ASL1的梯度正则如下所示，

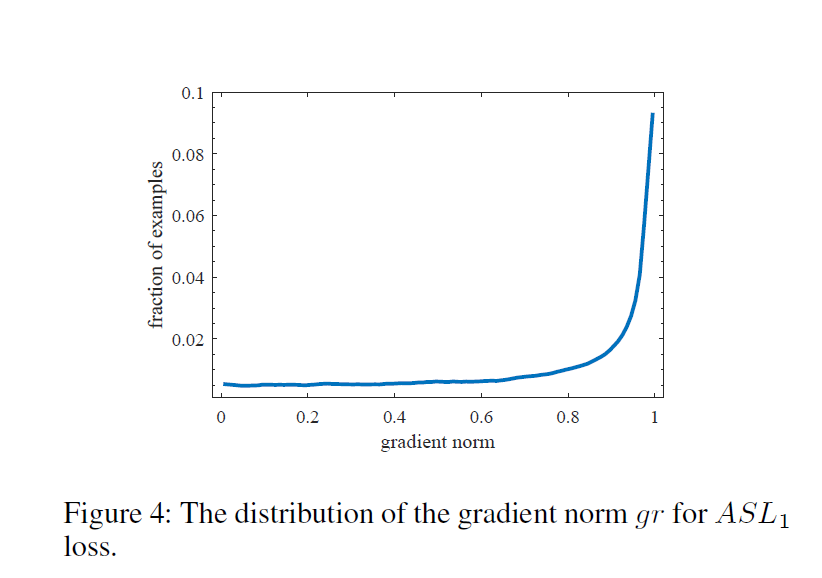
          其梯度分布如下图所示，从图中可以看出存在大量的异常点。而回归损失只作用在正样本中，因此，分类与回归的分布是不同的。

          应用GHM后的回归损失如下，

          SL1损失，ASL1损失及GHM的ASL1损失的梯度贡献图如下所示

 

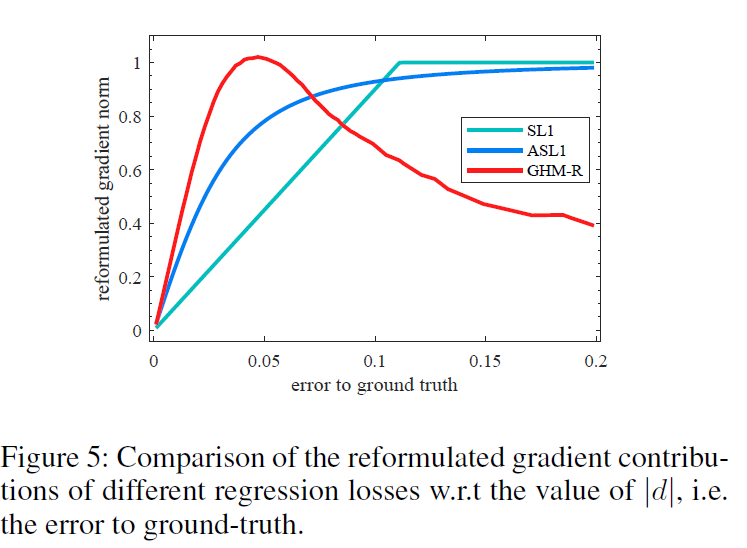
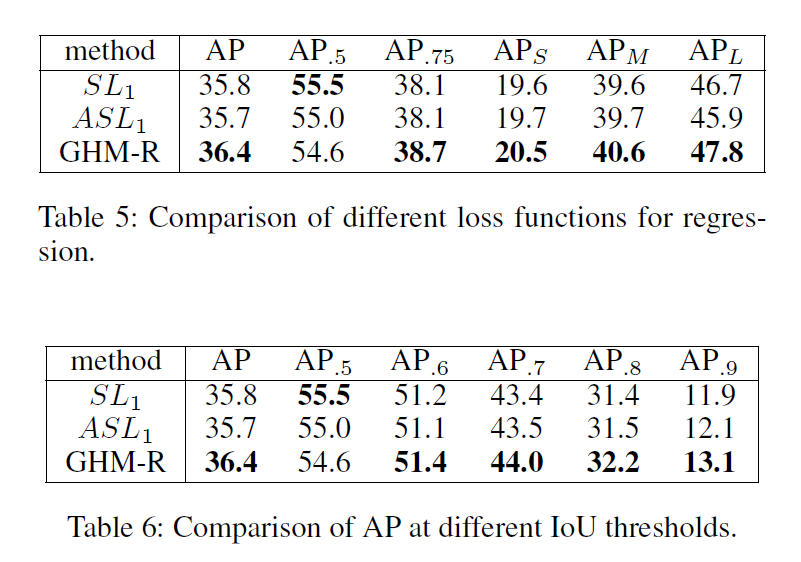
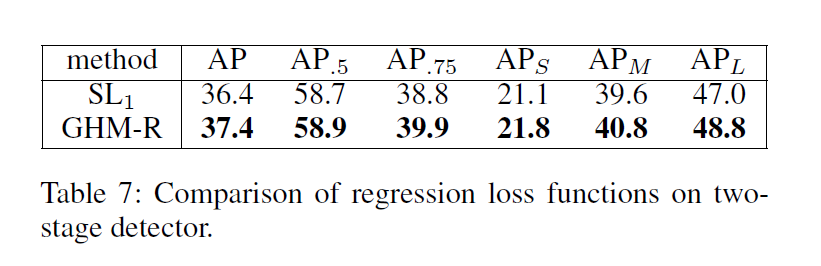
          在边界回归损失中，不是所有的简单样本都是不重要的，在分类中，一个简单样本通常是一个概率很低的背景区域，而且最终会被排除在候选之外。这类样本的改进对于精度毫无作用，但是在边界框的回归过程中，一个简单样本仍然偏离ground truth位置。任何样本的更好的预测将会直接提高最终候选框的质量。另外，高级的数据集更多关注的是定位的准确率。GHM-R损失可以通过提升easy样本的重要部分的权重同时降低异常点的权重来协调边界框回归中easy及hard 样本。

 实验

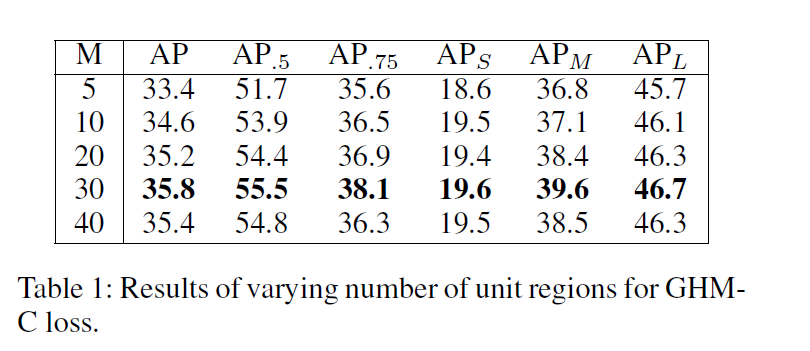
Reference

          [1][Chen et al. 2017] Chen, Z.; Badrinarayanan, V.; Lee, C.-Y.;and Rabinovich, A. 2017. Gradnorm: Gradient normalization for adaptive loss balancing in deep multitask networks.arXiv preprint arXiv:1711.02257.

          [2][Dai et al. 2016] Dai, J.; Li, Y.; He, K.; and Sun, J. 2016.R-fcn: Object detection via region-based fully convolutional
networks. In Advances in neural information processing systems,379–387.

          [3][Felzenszwalb, Girshick, and McAllester 2010]Felzenszwalb, P. F.; Girshick, R. B.; and McAllester,D. 2010. Cascade object detection with deformable part models. In Computer vision and pattern recognition (CVPR), 2010 IEEE conference on, 2241–2248. IEEE.
          [4][Fu et al. 2017] Fu, C.-Y.; Liu,W.; Ranga, A.; Tyagi, A.; and Berg, A. C. 2017. Dssd: Deconvolutional single shot detector.arXiv preprint arXiv:1701.06659.