神经网络是模拟人脑思维方式的数学模型。神经网络是智能控制的一个重要分支,人们针对控制过程提供了各种实现方式,在本节我们主要讨论一下采用单神经元实现PID控制器的方式。
1、单神经元的基本原理
单神经元作为构成神经网络的基本单位,具有自学习和自适应能力,且结构简单而易于计算。接下来我们讨论一下单神经元模型的基本原理。
(1)、单神经元模型
所谓单神经元模型,是对人脑神经元进行抽象简化后得到一种称为McCulloch-Pitts模型的人工神经元,如下图所示。
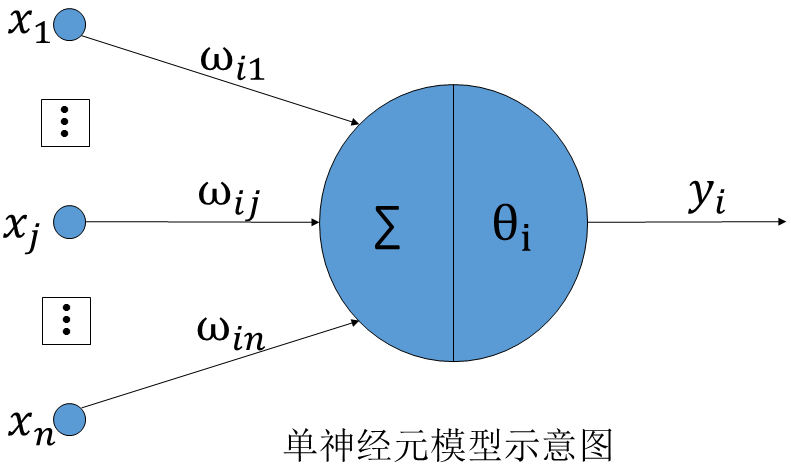
根据上图所示,对于第i个神经元,x1、x2、……、xN是神经元接收到的信息,ω1、ω2、……、ωN为连接强度,又称之为权。采用某种运算方式把输入信号的作用结合起来,得到他们总的结果,称之为“净输入”通常用neti表示。根据所采用的运算方式的不同,净输入有不同的表示形式,比较常用的是线性加权求和,其表达式如下:

其中,θi是神经元i的阈值。
而神经元i的输出yi可以表示为其当前状态的函数,这个函数我们称之为激活函数。一般表示如下:
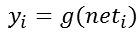
(2)、采用的学习规则
学习是神经网络的基本特征,而学习规则是实现学习过程的基本手段。学习规则主要实现对神经元之间连接强度的修正,即修改加权值。而学习过程可分为有监督学习和无监督学习两类。它们的区别简单的说,就是是否引入期望输出参与学习过程,引入了则称之为有督导学习。较为常用的学习规则有三种:
a、无监督Hebb学习规则
Hebb学习是一类相关学习,它的基本思想是:如果神经元同时兴奋,则它们之间的连接强度的增强与它们的激励的乘积成正比。以Oi表示单元i的激活值,以Oj表示单元j的激活值,以ωij表示单元j到单元i的连接强度,则Hebb学习规则可用下式表示:
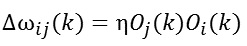
b、有监督Delta学习规则
在Hebb学习规则中,引入教师信号,将式Oj换成网络期望目标输出dj和网络实际输出Oj之差,即为有监督Delta学习规则,即:
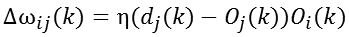
c、有监督Hebb学习规则
将无监督Hebb学习规则和有监督Delta学习规则两者结合起来,就组成有监督Hebb学习规则,即:
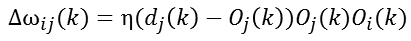
在以上各式中,η称之为学习速度。
2、单神经元PID的基本原理
在前面我们说明了单神经元的基本原理,接下来我们讨论如何将其应用的PID控制中。前面我们已经知道了神经元的输入输出关系,在这里我们考虑PID算法的增量型表达式:
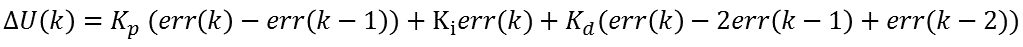
若是我们记:x1(k)=err(k),x2(k)=err(k)- err(k-1),x3(k)=err(k)- 2err(k-1)+err(k-2),同时将比例、积分、微分系数看作是它们对应的加权,并记为ωi(k)。同时我们引进一个比例系数K,则可将PID算法的增量型公式改为:
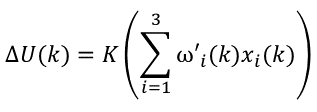
其中,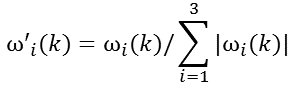
我们将PID的增量公式已经改为单神经元的输入输出表达形式,还需要引进相应的学习规则就可以得到单神经元PID控制器了。在这里我们采用有监督Hebb学习规则于是可以得到学习过程:
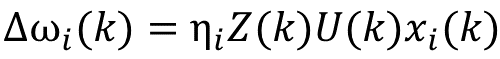
从学习规则的定义,我们知道在上式中,Z(k)= err(k)。而U(k)= U(k-1)+∆U(k),ω(k)= ω(k-1)+∆ω(k)。到这里实际上已经得到了单神经元PID的算法描述。
3、单神经元PID的软件实现
有了前面的准备,我们就可以开始编写基于单神经元的PID控制程序了。首先依然是定义一个单神经元的PID结构体:
1 /*定义结构体和公用体*/ 2 3 typedef struct 4 5 { 6 7 float setpoint; /*设定值*/ 8 9 float kcoef; /*神经元输出比例*/ 10 11 float kp; /*比例学习速度*/ 12 13 float ki; /*积分学习速度*/ 14 15 float kd; /*微分学习速度*/ 16 17 float lasterror; /*前一拍偏差*/ 18 19 float preerror; /*前两拍偏差*/ 20 21 float deadband; /*死区*/ 22 23 float result; /*输出值*/ 24 25 float output; /*百分比输出值*/ 26 27 float maximum; /*输出值的上限*/ 28 29 float minimum; /*输出值的下限*/ 30 31 float wp; /*比例加权系数*/ 32 33 float wi; /*积分加权系数*/ 34 35 float wd; /*微分加权系数*/ 36 37 }NEURALPID;
接下来在使用PID对象之前依然需要对它进行初始化操作,以保证在未修改参数的值之前,PID对象也是可用的。这部分初始化比较简单,与前面的各类PID对象的初始化类似。
1 /* 单神经元PID初始化操作,需在对vPID对象的值进行修改前完成 */ 2 3 /* NEURALPID vPID,单神经元PID对象变量,实现数据交换与保存 */ 4 5 /* float vMax,float vMin,过程变量的最大最小值(量程范围) */ 6 7 void NeuralPIDInitialization(NEURALPID *vPID,float vMax,float vMin) 8 9 { 10 11 vPID->setpoint=vMin; /*设定值*/ 12 13 14 15 vPID->kcoef=0.12; /*神经元输出比例*/ 16 17 vPID->kp=0.4; /*比例学习速度*/ 18 19 vPID->ki=0.35; /*积分学习速度*/ 20 21 vPID->kd=0.4; /*微分学习速度*/ 22 23 24 25 vPID->lasterror=0.0; /*前一拍偏差*/ 26 27 vPID->preerror=0.0; /*前两拍偏差*/ 28 29 vPID->result=vMin; /*PID控制器结果*/ 30 31 vPID->output=0.0; /*输出值,百分比*/ 32 33 34 35 vPID->maximum=vMax; /*输出值上限*/ 36 37 vPID->minimum=vMin; /*输出值下限*/ 38 39 vPID->deadband=(vMax-vMin)*0.0005; /*死区*/ 40 41 42 43 vPID->wp=0.10; /*比例加权系数*/ 44 45 vPID->wi=0.10; /*积分加权系数*/ 46 47 vPID->wd=0.10; /*微分加权系数*/ 48 49 }
初始化之后,我们就可以调用该对象进行单神经元PID调节了。前面我们已经描述过算法,下面我们来实现它:
1 /* 神经网络参数自整定PID控制器,以增量型方式实现 */ 2 3 /* NEURALPID vPID,神经网络PID对象变量,实现数据交换与保存 */ 4 5 /* float pv,过程测量值,对象响应的测量数据,用于控制反馈 */ 6 7 void NeuralPID(NEURALPID *vPID,float pv) 8 9 { 10 11 float x[3]; 12 13 float w[3]; 14 15 float sabs 16 17 float error; 18 19 float result; 20 21 float deltaResult; 22 23 24 25 error=vPID->setpoint-pv; 26 27 result=vPID->result; 28 29 if(fabs(error)>vPID->deadband) 30 31 { 32 33 x[0]=error; 34 35 x[1]=error-vPID->lasterror; 36 37 x[2]=error-vPID->lasterror*2+vPID->preerror; 38 39 40 41 sabs=fabs(vPID->wi)+fabs(vPID->wp)+fabs(vPID->wd); 42 43 w[0]=vPID->wi/sabs; 44 45 w[1]=vPID->wp/sabs; 46 47 w[2]=vPID->wd/sabs; 48 49 50 51 deltaResult=(w[0]*x[0]+w[1]*x[1]+w[2]*x[2])*vPID->kcoef; 52 53 } 54 55 else 56 57 { 58 59 deltaResult=0; 60 61 } 62 63 64 65 result=result+deltaResult; 66 67 if(result>vPID->maximum) 68 69 { 70 71 result=vPID->maximum; 72 73 } 74 75 if(result<vPID->minimum) 76 77 { 78 79 result=vPID->minimum; 80 81 } 82 83 vPID->result=result; 84 85 vPID->output=(vPID->result-vPID->minimum)*100/(vPID->maximum-vPID->minimum); 86 87 88 89 //单神经元学习 90 91 NeureLearningRules(vPID,error,result,x); 92 93 94 95 vPID->preerror=vPID->lasterror; 96 97 vPID->lasterror=error; 98 99 }
前面的算法分析中,我们就是将增量型PID算法的表达式转化为单神经元PID公式的。二者最根本的区别在于单神经元的学习规则算法,我们采用了有监督Hebb学习规则来实现。
1 /*单神经元学习规则函数*/ 2 3 static void NeureLearningRules(NEURALPID *vPID,float zk,float uk,float *xi) 4 5 { 6 7 vPID->wi=vPID->wi+vPID->ki*zk*uk*xi[0]; 8 9 vPID->wp=vPID->wp+vPID->kp*zk*uk*xi[1]; 10 11 vPID->wd=vPID->wd+vPID->kd*zk*uk*xi[2]; 12 13 }
至此,单神经元PID算法就实现了,当然有很多进一步优化的方式,都是对学习规则算法的改进,因为改进了学习规则,自然就改进了单神经元PID算法。
4、单神经元PID总结
前面我们已经分析并实现了单神经元PID控制器,在本节我们来对它做一个简单的总结。
与普通的PID控制器一样,参数的选择对调节的效果有很大影响。对单神经元PID控制器来说,主要是4个参数:K、ηp、ηi、ηd,我们总结一下相关参数选取的一般规律。
(1)对连接强度(权重ω)初始值的选择并无特殊要求。
(2)对阶跃输入,若输出有大的超调,且多次出现正弦衰减现象,应减少增益系数K,维持学习速率ηp、ηi、ηd不变。若上升时间长,而且无超调,应增大增益系数K以及学习速率ηp、ηi、ηd。
(3)对阶跃输入,若被控对象产生多次正弦衰减现象,应减少比例学习速率ηp,而其它参数保持不变。
(4)若被控对象响应特性出现上升时间短,有过大超调,应减少积分学习速率ηi,而其它参数保持不变。
(5)若被控对象上升时间长,增大积分学习速率ηi又会导致超调过大,可适当增加比例学习速率ηp,而其它参数保持不变。
(6)在开始调整时,微分学习速率ηd应选择较小值,在调整比例学习速率ηp、积分学习速率ηi和增益系数K使被控对象达到较好特性后,再逐渐增加微分学习速率ηd,而其它参数保持不变。
(7)K是系统最敏感的参数,K值的变化相当于P、I、D三项同时变化。应在开始时首先调整K,然后再根据需要调整学习速率。
在单神经元PID控制器中,上述这些参数对调节效果的影响如何呢?一般情况下具有如下规律。
(1)在积分学习率、微分学习率不变的情况下,比例系数学习率越大则超调量越小,但是响应速度也会越慢;
(2)在比例学习率、微分学习率不变的情况下,积分系数学习率越大则响应会越快,但是超调量也会越大。
(3)在比例学习率、积分学习率不变的情况下,微分学习率对单神经元PID控制器的控制效果影响不大。
最后我们需要明白,单神经元PID算法是利用单神经元的学习特性,来智能的调整PID控制过程。单神经元可以实现自学习,这正好可以弥补传统PID算法的不足。正如前面所说,学习是它的最大特点,那么不同的学习算法对其性能的影响会很大,所以改进学习规则算法对提高性能有很大帮助。
欢迎关注:
