pca:principal component analysis,常见的降维技术
生成一组多元正态分布的数据,两个随机分布的协方差矩阵:cov(x,x)=5 cov(x,y)=5 cov(y,y)=5 cov(y,x)=25
import numpy as np
import matplotlib.pyplot as plt
mean = [20, 20]
cov = [[5, 5], [5, 25]]
x, y = np.random.multivariate_normal(mean, cov, 500).T
plt.plot(x, y, '.')
plt.axis([0, 40, 0, 40])
plt.xlabel('feature 1')
plt.ylabel('feature 2')
plt.show()
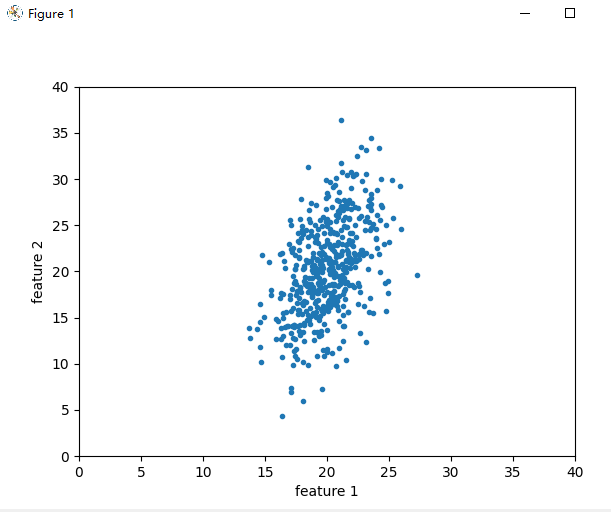
展示出两个特征向量,一个是数据分布最大方向,也称第一主成分,另一个是方差方向,第二主成分。
import numpy as np
import matplotlib.pyplot as plt
import cv2
mean = [20, 20]
cov = [[5, 5], [5, 25]]
X = np.random.multivariate_normal(mean, cov, 500)
x, y = X.T
mu, eig = cv2.PCACompute(X, np.array([]))
plt.plot(x, y, '.', zorder=1)
plt.quiver(mean[0], mean[1], eig[0, 0], eig[0, 1],zorder=3, scale=0.2, units='xy')
plt.quiver(mean[0], mean[1], eig[1, 0], eig[1, 1],zorder=3, scale=0.2, units='xy')
plt.axis([0, 40, 0, 40])
plt.xlabel('feature 1')
plt.ylabel('feature 2')
plt.show()

利用opencv的PCAProject来旋转数据
import numpy as np
import matplotlib.pyplot as plt
import cv2
mean = [20, 20]
cov = [[5, 5], [5, 25]]
X = np.random.multivariate_normal(mean, cov, 500)
x, y = X.T
mu, eig = cv2.PCACompute(X, np.array([]))
X2 = cv2.PCAProject(X,mu,eig)
# plt.plot(x, y, '.', zorder=1)
# plt.quiver(mean[0], mean[1], eig[0, 0], eig[0, 1],zorder=3, scale=0.2, units='xy')
# plt.quiver(mean[0], mean[1], eig[1, 0], eig[1, 1],zorder=3, scale=0.2, units='xy')
plt.plot(X2[:,0],X2[:,1],'.')
plt.axis([-20, 20, -20, 20])
plt.xlabel('feature 1')
plt.ylabel('feature 2')
plt.show()
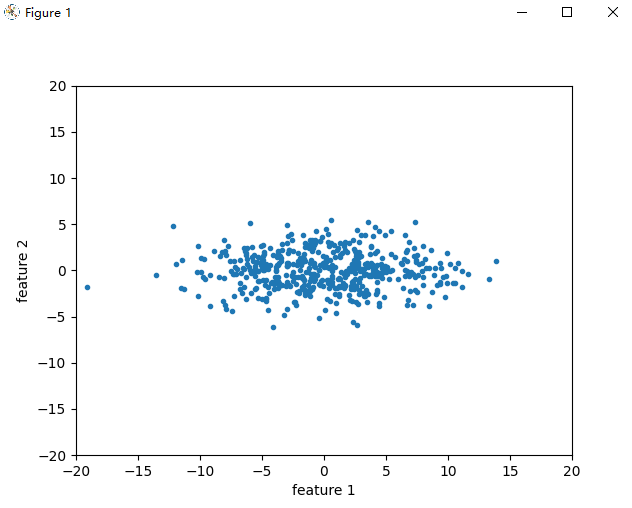
当人,箭头方向是还是原来的(⊙ˍ⊙)
