迭代器 Iterator 是什么?
Java容器的顶部接口就是Iterator。是一个可以遍历集合的对象,为各种容器提供了公共的操作接口,隔离对容器的遍历操作和底层实现,从而解耦。
- java迭代器查找的唯一操作就是依靠调用next,而在执行查找任务的同时,迭代器的位置也在改变.
- Iterator迭代器remove方法会删除上次调用next方法返回的元素.这也意味之remove方法和next有着很强的依赖性.如果在 调用remove之前没有调用next是不合法的 .这个接口衍生出了,java集合的迭代器.java集合的迭代器使用
{
boolean hasNext() //如果仍有元素可以迭代,则返回 true。
E next() //返回迭代的下一个元素。
void remove() //删除
default void forEach //实现了迭代器接口的类才可以使用forEach
}
查看最新图片,请点击:https://www.processon.com/apps/58bd73cfe4b0f944a6660f38

迭代器 Iterator 怎么使用?
易错点:Iterator调用remove之前没有调用next是不合法的
class test {
public static void run() {
List<Integer> list = new LinkedList<>();
list.add(1);
list.add(2);
list.add(3);
list.add(3);
//依靠这个方法生成一个java集合迭代器<--在Colletion接口中的方法,被所有集合实现.
Iterator<Integer> iterator = list.iterator();
// iterator.remove();报错java.lang.IllegalStateException
iterator.next();
iterator.remove();//不报错,删掉了1
System.out.println(list);//AbstractCollection类中实现的toString让list可以直接被打印出来
while (iterator.hasNext()) {//迭代器,hasNext()集合是否为空
Integer a = iterator.next();//可以用next访问每一个元素
System.out.println(a);//2,3,3
}
for (int a : list) {//也可以使用foreach
System.out.println(a);//2,3,3
}
}
public static void main(String[] args) {
run();
}
}
当然你也会有点好奇,为什么 remove 方法前面必须跟着一个next方法.其实这个只能这么解释.
迭代器的next方法的运行方式并不是类似于数组的运行方式.
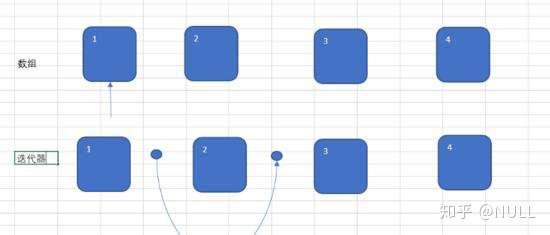
当然,这张图主要是让你理解一下.
数组的指针指向要操作的元素上面,而迭代器却是将要操作的元素放在运动轨迹中间.
本质来讲,迭代器的指针并不是指在元素上,而是指在元素和元素中间.
假设现在调用remove().被删除的就是2号元素.(被迭代器那个圆弧笼盖在其中的那个元素).如果再次调用,就会报错,因为圆弧之中的2号元素已经消失,那里是空的,无法删除.
参考
不眠不休不写bug:java集合详解