原题链接:
我的来源:2012.11.11CSUST Warm Up(Preparing for the 2013 )(personal):http://acm.hust.edu.cn:8080/judge/contest/view.action?cid=16690#problem/I
Description
In the picture below you can see a triangle ABC. Point D, E and F divides the sides BC, CA and AB into ratio 1:2 respectively. That is CD=2BD, AE=2CE and BF=2AF. A, D; B, E and C, F are connected. AD and BE intersects at P, BE and CF intersects at Q and CF and AD intersects at R.

So now a new triangle PQR is formed. Given triangle ABC your job is to find the area of triangle PQR.
Input
First line of the input file contains an integer N (0<N<1001) which denotes how many sets of inputs are there. Input for each set contains six floating-point number Ax, Ay, Bx, By, Cx, Cy. (0≤Ax, Ay, Bx, By, Cx,Cy ≤10000) in one line line. These six numbers denote that the coordinate of points A, B and C are (Ax, Ay), (Bx, By) and (Cx, Cy) respectively. A, B and C will never be collinear.
Output
For each set of input produce one line of output. This one line contains an integer AREA. Here AREA is the area of triangle PQR, rounded to the nearest integer.
Sample Input
2
3994.707 9251.677 4152.916 7157.810 5156.835 2551.972
6903.233 3540.932 5171.382 3708.015 213.959 2519.852
Sample Output
98099
206144
题目大意:任意△ABC中F、D、E分别为三边的三等分点中点,将其分别与对应的顶点相连,得到一个新的△RPQ。
现在给出△ABC的坐标,求△RPQ的面积
解题思路:用叉积求出△ABC的面积三角形 ABC 的面积= |AxBy - AyBx + BxCy - ByCx + CxAy - CyAx| / 2
叉积: Ax Ay 1
Bx By 1 = AxBy - AyBx + BxCy - ByCx + CxAy - CyAx
Cx Cy 1
可以证明:S△BPQ :S△ABC = 1 : 7
PS:只会证明正三角形的,so这道题目也算是水过的了ORz。。。
第一个证明是正三角形的,第二个证明是普通三角形的(感谢江,全能的数学啊!)
下面给出正三角形的证明: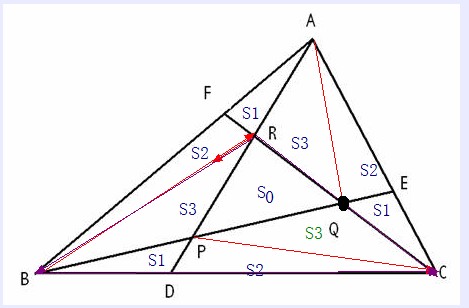
如图所示:1、由正三角形的对称性知道S△AFR=S△BDP=S△CQE=S1
S△BFR=S△CDP=S△AQE=S2
S△BPR=S△AQR=S△CPQ=S3
2、△ABC中D为边BC的三等分点,BD :BC = 1 : 3 所以S△ABD :S△ABC = 1 : 3
3*S△ABD=S△ABD+S△BCE+S△CAF=S△ABC易得3*S1=S0
3、△BPC中BD : DC =1 : 2,所以S1:S2=1 :2,所以S1+S2=S0
4、在△BRC中S△BRQ=S0+S3
S△BCQ=(S1+S2)+S3=S0+S3
所以:S△BRQ=S△BCQ,即Q为RC的中点,那么在△PRC中可知S0=S3
综上所述:S0=S3=S1+S2,所以S0 :S△ABC=1 :7
普通三角形证明方法:

如图所示作AG∥BC交BE延长线于点G,作DH∥AB交CF于点H,
则得:AG:BC=AE:EC=1:2,AP:PD=AG:BD=3:4 *****************(1)
又由于DH:BF=1:3,DH:AF=1:6,
所以DR:AR=1:6,DR:DA=1:7, ********************************(2)
/****************************************************************************************************
PS:到了此处如果,不追究严格的论证方法,应该可以直接看出:
S△CDR=1/7S△BFC=1/21S△ABC,
因此S△PQR:S△ABC=1:7 即:S△PQR=1/7S△ABC=1/7
/*****************************************************************************************************
下面还是给出严格的证明过程:
由(1)(2)有AP:PR = 3 :3 即 P为AR的中点。
同理可得Q为BP中点,R为CQ中点。
连接AQ、CP、BR。
在△AQR中,P为AR中点,所以由同底等高得S△AQP=S△RQP
同理有S△PQR=S△BQR=S△CPR=S△AQR **************************(3)
因为F、D、E分别为三角形三条边的三等分点
所以S△ABE=S△CBF=S△ADC=1/3*S△ABC (底在同一条线上,高相等)
所以S△ABE+S△CBF+S△ADC=S△ABC ****************************(4)
而(4)中三个小三角形△BFQ、△AEP、△CDR加了两次,但是△PQR没有加
所以△BFQ + △AEP + △CDR = △PQR ******************************(5)
而在△BRC中DC : BC = 1 :3
得到S△CDR :S△BCR= 1 :3
同理S△BFQ :S△BAQ=1 :3
S△AEP :S△ACP= 1 :3
所以由(5)有S△BAQ + S△ACP + S△BCR = 3*(△BFQ + △AEP + △CDR)
=3*S △PQR ***********************(6)
由(3)(6)得到S△PQR=1/7S△ABC
#include<stdio.h>
int main()
{
int n;
double Ax,Ay,Bx,By,Cx,Cy;
double are;
while(scanf("%d",&n)!=EOF)
{
while(n--)
{
scanf("%lf%lf%lf%lf%lf%lf",&Ax,&Ay,&Bx,&By,&Cx,&Cy);
are=(Ax*By+Bx*Cy+Cx*Ay-Ay*Bx-By*Cx-Cy*Ax)/(2*7);
are>=0?are:-are;
printf("%.0lf\n",are);
}
}
return 0;
}