LeetCode77. 组合

题目

给定两个整数 n 和 k，返回 1 ... n 中所有可能的 k 个数的组合。

分析

本题属于回溯中的组合问题

首先回溯问题的整体模板，如下（参考代码随想的Carl）

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

递归函数的参数不仅要有题目中的 N 和 K，还要记录本层递归中每次递归搜索的位置。每次从集合中选取元素，可选择的范围随着选择的进行而收缩，调整可选择的范围，就是要靠startIndex

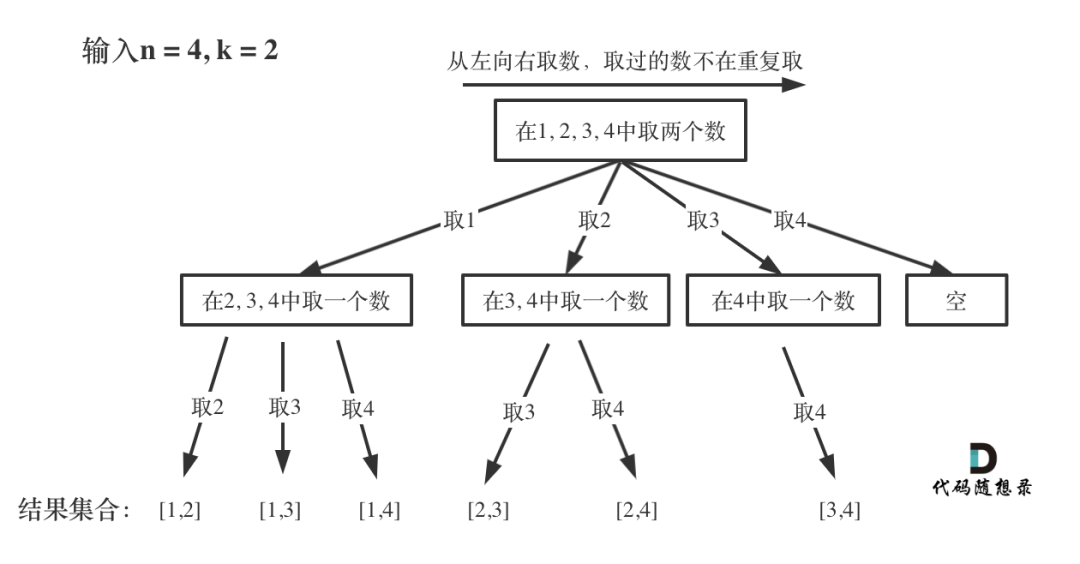
 相当于对原本的搜索树修剪，越搜索树宽度越窄，因为有些结果在之前就搜索过了。

代码

class Solution {
public:
    vector<int>path;//存放单条路径的结果
    vector<vector<int>>res; //存放路径结果的集合

    void backtracking(int n,int k,int startIndex){
        //终止条件
        if(path.size() == k){
            res.push_back(path);//存放结果
            return;
        }
        //for循环对搜索树横向遍历，递归对搜索树纵向遍历
        //for循环的开始搜索位置是strartIndex
        for(int i = startIndex;i <= n;i++){
            path.push_back(i);//对节点进行处理
            backtracking(n,k,i+1);//递归
            path.pop_back();//回溯，撤销对节点的处理
        }
    }
    vector<vector<int>> combine(int n, int k) {
        backtracking(n,k,1);
        return res;
    }
};

其实这样并不算最优，因为还可以将搜索树进行剪枝

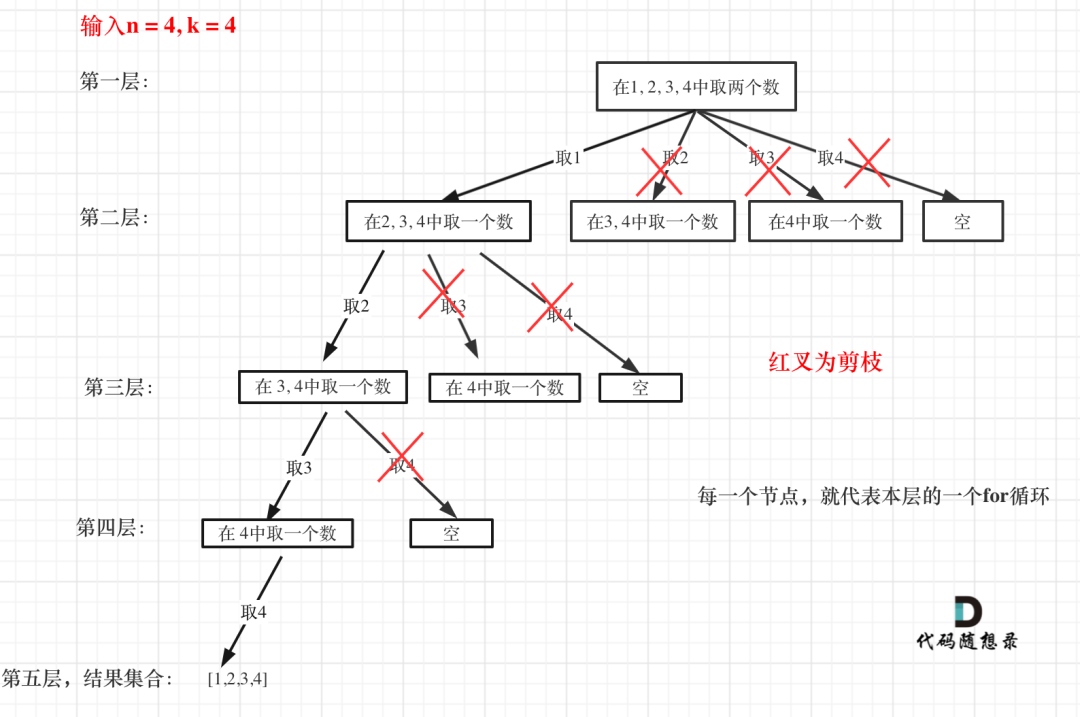
 for 循环选择的起始位置之后的元素个数 已经不足我们需要的元素个数，就没有必要搜索，直接剪掉。

所以优化后的代码如下：

class Solution {
private:
    vector<vector<int>> result; 
    vector<int> path;
    void backtracking(int n, int k, int startIndex) {
        if (path.size() == k) {
            result.push_back(path);
            return;
        }
        for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) { // 优化的地方
            path.push_back(i); // 处理节点 
            backtracking(n, k, i + 1);
            path.pop_back(); // 回溯，撤销处理的节点
        }
    }
public:

    vector<vector<int>> combine(int n, int k) {
        backtracking(n, k, 1);
        return result;
    }
};