LeetCode491. 递增子序列

题目

给定一个整型数组, 你的任务是找到所有该数组的递增子序列，递增子序列的长度至少是2。

1. 给定数组的长度不会超过15。
2. 数组中的整数范围是 [-100,100]。
3. 给定数组中可能包含重复数字，相等的数字应该被视为递增的一种情况。

法一分析

自己首先想法：本题和取子集的题目差不多，但不能通过排序+used数组来去重，因为是递增子序列，不可破坏原本子序列次序。我是通过把每次结果放到 set 里面来把结果进行去重。何时将结果加入 set ? 它和取子集问题一样，不必到叶子结点，每层都取，也就是进入下层后要将上层结果存入 set 中。最后再把set 中的结果放入 res中。

法一代码

class Solution {
public:
    vector<int>path;
    vector<vector<int>>res;
    set<vector<int>>s;
    bool check(vector<int>nums){
        for(int i = 1;i < nums.size();i++){
            if(nums[i] < nums[i-1]) return false;
        }
        return true;
    }
    void backtracking(vector<int> nums,int startIndex){
        if(check(path) && path.size() >= 2){
            s.emplace(path);
            //res.push_back(path);
        }
            
        if(!check(path)) return;

        for(int i = startIndex;i < nums.size();i++){
            path.push_back(nums[i]);
            backtracking(nums,i+1);
            path.pop_back();
        }
    }

    vector<vector<int>> findSubsequences(vector<int>& nums) {
        backtracking(nums,0);
        for(auto it:s){
            res.push_back(it);
        }
        return res;
    }
};

上面set可使用unordered_set

法二分析 按照Carl的思路

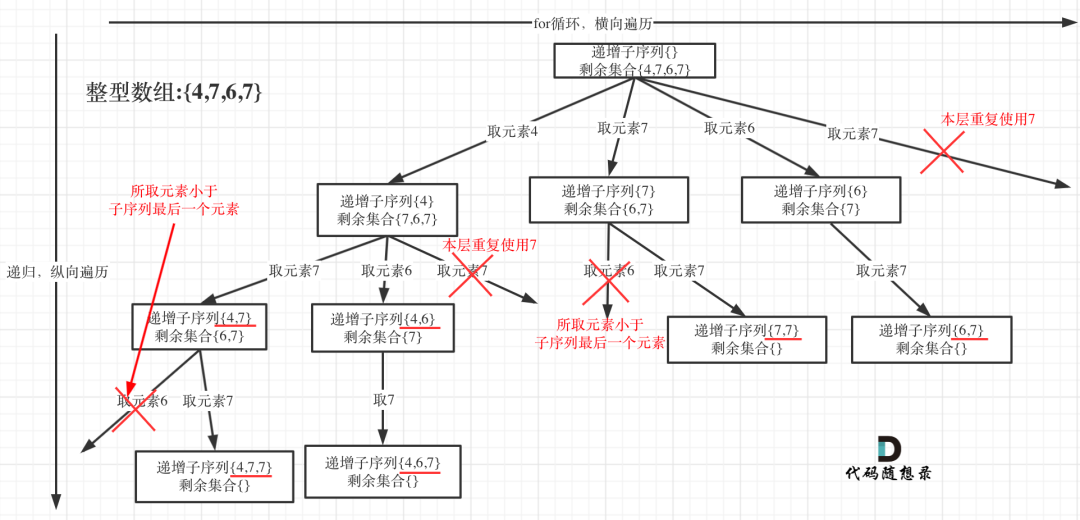
直接排除可能重复的情形：只要同层重复使用元素，递增子序列就会重复 。注意要与 求子集问题（二）中去重区别。子集问题二是先排序然后看相邻元素是否重复使用。

判断递增：如果选取的元素小于子序列里面最后一个元素，那么pass，着说明了不是递增。去重逻辑代码如下：

if ((!path.empty() && nums[i] < path.back())
        || uset.find(nums[i]) != uset.end()) {
        continue;
}

注意 本题的数据范围为 [-100,100]，数据范围小，可以直接用数组进行哈希，这样比set快。 

法二代码

class Solution {
public:
    vector<int>path;
    vector<vector<int>>res;
    
    void backtracking(vector<int> nums,int startIndex){
        if(path.size() > 1) {
            res.push_back(path);
        }
        int used[201] = {0}; // 用数组来去重，数据范围是-100，100

        for(int i = startIndex;i < nums.size();i++){
            //非递增或者重复直接pass
            if((!path.empty() && path.back() > nums[i])
                || used[100+nums[i]] == 1) continue;
            
            used[100+nums[i]] = 1; //表示这个元素使用过了
            path.push_back(nums[i]);
            backtracking(nums,i+1);
            path.pop_back();
            //注意不在这里恢复used数值，在下一层恢复used数值
        }
    }

    vector<vector<int>> findSubsequences(vector<int>& nums) {
        backtracking(nums,0);
        return res;
    }
};

注意上面代码，used数组恢复位置，本层不恢复。