图像处理的过程中经常要用到,至于一维卷积我就不罗嗦了,大家都应该知道
设矩阵A和矩阵B, A的行数和列数分别为Mr, Mc, B的行数和列数分别为Nr, Nc,
则有:
且s,t满足条件 0≤ s < Mr+Nr-1, 0 ≤ t < Mc+Nc-1;
下面看示例:
仔细看一下就知道,M1刚好是M2的180度翻转, 如果按照一维形式展开的话也是一样的,
通常我们对图像进行处理时也要边缘进行对齐的,以取得我们所要的图片。
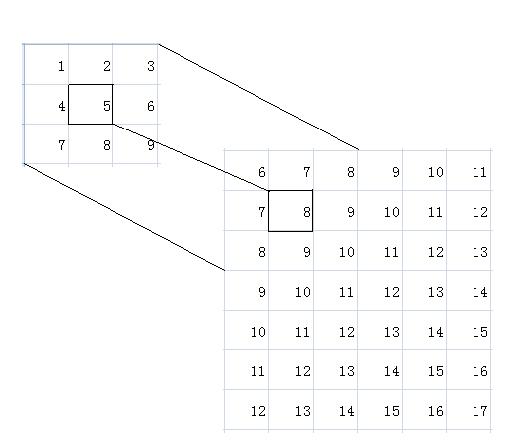
假设小图框为变换矩阵M1,大图框为位图,我们可以对C(2,2)进行计算:
C(2,2) = 1*6 + 2*7+3*8 + 4*7 + 5*8 + 6*9 + 7*8+8*9+9*10 = 384
如果元素的边界部分为空,就用0补足, 例如C(1,1), C(0,0)等。