题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=4767
题意：求集合{1, 2, 3, ..., n}有多少种划分情况bell[n]，最后结果bell[n] mod 95041567.
分析：首先了解三个概念：贝尔数 第二类斯特灵数 中国剩余定理
贝尔数是指基数为n的集合的划分方法的数目。
贝尔数适合递推公式：
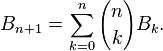
每个贝尔数都是"第二类Stirling数"的和
贝尔数满足两个公式：（p为质数）
1) B[n+p] = B[n] + B[n+1] （mod p） ;
2) B[p^m+n] = m*B[n] + B[n+1] （mod p） .
将95041567质因数分解发现，95041567 = 31*37*41*43*47
所以B[n]%95041567可以分解为 B[n]%p(p=31,41,43,47)，
我们可以先求出B[n] mod p[i]的值a[i],这样问题就转化为 X=a[i](mod p[i])，
很明显这是几个一次同余方程，最后用中国剩余定理合并就可以了。
那要怎么求B[n]%p[i]呢？
利用上面的公式（1），我们发现这是 一个递推式，所以可以利用矩阵法来求解。
我们可以构造一个大小为当前p*p的矩阵。
这样我们就可以求出任意的B[n]了
我们可以先用贝尔数递推公式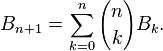求出前50个贝尔数，因为p[i]<50，所以对于大于p[i]的贝尔数，由上面的矩阵法可以求得。
比如：| 1 1 0 0 .... 0 0 | | B[1] | | B[1+p] |
| 0 1 1 0 .... 0 0 | | B[2] | | B[2+p] |
| 0 0 1 1 .... 0 0 | | B[3] | | B[3+p] |
| .... .... .... .... | * | ..... | = | ..... |
| 0 0 0 0 .... 1 1 | | B[p-1] | | B[2p-1]|
| 1 1 0 0 .... 0 1 | | B[p] | | B[2p] |
若n=i+p,则只需求一次A*C=D，然后输出D[n-p]即D[i]就行了，
比如p[0]=31，如要求B[32]=B[1+31]，只需求一次A*C=D,然后输出D[1]，求B[51]则输出D[20]。
那么
若n=i+p^m,这只需求A^m*C=D，然后输出D[i]即可
到此算法结束
总结一下：
先用贝尔数递推公式求出前50个贝尔数，然后用矩阵快速幂分别求出bell[n]%p[i]赋给a[i]，然后用中国剩余定理合并结果就可以求出bell[n]%95041567了。
AC代码如下：
1 #include<stdio.h> 2 #include<string.h> 3 #define LL __int64 4 int w[5]={31,37,41,43,47}; 5 LL c[50][50][5],bell[50][5]; 6 LL a[5]; 7 struct Matrix{ 8 LL m[50][50]; 9 }; 10 void init() 11 { 12 int i,j,k; 13 for(k=0;k<5;k++) 14 { 15 c[0][0][k]=1; 16 for(i=1;i<50;i++) //c[i][j][k] 表示c(i,j)%w[k] 17 { 18 c[i][0][k]=c[i][i][k]=1; 19 for(j=1;j<i;j++) 20 c[i][j][k]=(c[i-1][j-1][k]+c[i-1][j][k])%w[k]; 21 } 22 } 23 // 预处理出前50项分别取模的大小 24 for(k=0;k<5;k++) 25 { 26 bell[0][k]=1; 27 for(i=1;i<50;i++) 28 { 29 bell[i][k]=0; 30 for(j=0;j<i;j++) 31 { 32 bell[i][k]=(bell[i][k]+c[i-1][j][k]*bell[j][k])%w[k]; 33 } 34 } 35 } 36 } 37 LL exgcd(LL a,LL b,LL &x,LL &y) //扩展欧几里得 38 { 39 if(b==0) 40 { 41 x=1; y=0; 42 return a; 43 } 44 LL d=exgcd(b,a%b,x,y); 45 LL t=x; 46 x=y; 47 y=t-a/b*y; 48 return d; 49 } 50 LL CRT(int k) //中国剩余定理 51 { 52 LL i,N=1,ans=0; 53 LL t,x,y,d; 54 for(i=0;i<k;i++) 55 N*=w[i]; 56 for(i=0;i<k;i++) 57 { 58 t=N/w[i]; 59 d=exgcd(t,w[i],x,y); 60 ans=(ans+x*t*a[i])%N; 61 } 62 return (ans+N)%N; 63 } 64 Matrix mul(Matrix x,Matrix y,int n,int mod) //矩阵乘法 65 { 66 int i,j,k; 67 Matrix tmp; 68 memset(tmp.m,0,sizeof(tmp.m)); 69 for(i=1;i<=n;i++) 70 for(j=1;j<=n;j++) 71 for(k=1;k<=n;k++) 72 { 73 tmp.m[i][j]+=(x.m[i][k]*y.m[k][j])%mod; 74 tmp.m[i][j]%=mod; 75 } 76 return tmp; 77 } 78 Matrix quickpow(Matrix res,Matrix A,int k,int n,int mod) //矩阵快速幂模 79 { 80 int i; 81 memset(res.m,0,sizeof(res.m)); 82 for(i=1;i<=n;i++) 83 res.m[i][i]=1; 84 while(k) 85 { 86 if(k&1) 87 res=mul(res,A,n,mod); 88 A=mul(A,A,n,mod); 89 k>>=1; 90 } 91 return res; 92 } 93 LL BellNumber(int n,int p) //求bell[n][p]即bell[n]%w[p] 94 { 95 int i; 96 if(n<50) 97 return bell[n][p]; 98 Matrix A,origin,ans; 99 memset(A.m,0,sizeof(A.m)); 100 memset(origin.m,0,sizeof(origin.m)); 101 for(i=1;i<w[p];i++) 102 A.m[i][i]=A.m[i][i+1]=1; 103 A.m[w[p]][1]=1; 104 A.m[w[p]][2]=1; 105 A.m[w[p]][w[p]]=1; 106 for(i=1;i<=w[p];i++) 107 origin.m[i][1]=bell[i][p]; 108 LL cnt=n/w[p]; 109 n=n-w[p]*cnt; 110 Matrix res; 111 res=quickpow(res,A,cnt,w[p],w[p]); 112 ans=mul(res,origin,w[p],w[p]); 113 return ans.m[n][1]; 114 } 115 void solve(int n) 116 { 117 int i; 118 for(i=0;i<5;i++) 119 a[i]=BellNumber(n,i); //bell[n]mod各个质数的值 120 LL ans=CRT(5); 121 printf("%I64d ",ans); 122 } 123 int main() 124 { 125 int t,n; 126 init(); 127 scanf("%d",&t); 128 while(t--) 129 { 130 scanf("%d",&n); 131 solve(n); 132 } 133 return 0; 134 }