设：n为特征数量，m为样本数量，x(i)为向量，就是一个样本的所有特征
现在我们的特征数量变多了，预测式自然也改变了 变为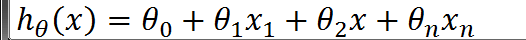
则
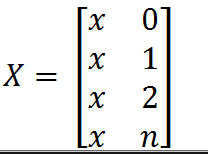
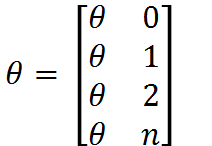唯度都为n+1
那么预测公式就为
代价函数为
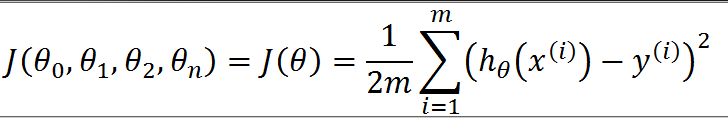
我们约定x_0=1，那么当特征数量（n>=1)时，我们进行下面这个公式进行梯度下降，直到收敛
{
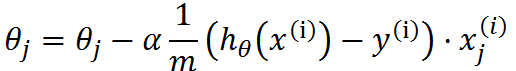
j=（0,1,2,3,......,n)
}
但是这样有的时候我们会遇到麻烦，在特征的大小差别很大的时候，梯度下降速度会十分的慢，所以我们需要用到特征缩放。
特征缩放的目的是使所有的x处于同一范围内，也就是-1<=x<=1（其实非常接近也是可以的），可以对x中的x进行等比例缩放。
均值归一化：xi-ui(为平均数)/s s为xi的范围（最大值-最小值）
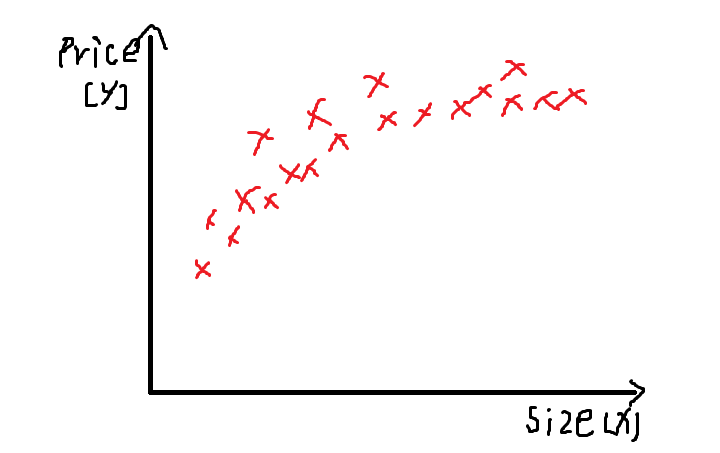
对于这么一组数据来说，直线不够吻合，抛物线不符合实际，所以可以试试size的3次方
x1=size,x2=(size)^2,x3=(size)^3
在此时，特征处理就显得尤为重要，因为你看100^3=1000000,1000^3=1000000000，并且对于这组数据x1=size，x2=sqrt（size）可能会更吻合。所以我们在创建模型时有多种特征可选择，选择不听的特征可能会有更好的模型。