算法导论学习-binary search tree

1. 概念：

Binary-search tree（BST）是一颗二叉树，每个树上的节点都有<=1个父亲节点，ROOT节点没有父亲节点。同时每个树上的节点都有[0,2]个孩子节点(left child AND right child)。每个节点都包含有各自的KEY值以及相应的satellite data。其中KEY是几种BST基本操作的主要操作对象。

 

2. BST的特别性质：

BST任何一颗子树上的三个节点left, parent, right. 满足条件left.key<parent.key<=right.key，一颗典型的BST如下图所示：

　　　　　　　　　　　　　　

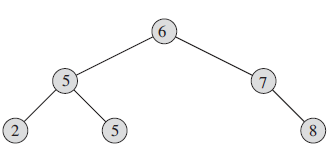
观察之后不难发现如果对BST进行PREORDER walk(先序遍历)，得到：2, 5, 5, 6, 7, 8 刚好是升序排列。

P.S 所谓PREORDER walk，就是要访问以ROOT为根的树，先要访问ROOT.left, 然后访问ROOT, 最后访问ROOT.right。

用pseudocode的形式的话，就是这样： 

PREORDER-WALK(x)

1 if(x!=NIL) 

2　　 PREORDER-WALK(x.left)

3 　　print x.key

4　　 PREORDER-WALK(x.right)

3. BST的几种基本操作：

SEARCH, MINIMUM, MAXIMUM, PREDECESSOR, SUCCESSOR, INSERT, and DELETE.

2.1 SEARCH：

TREE-SEARCH(x, k)
INPUT: BST ROOT node, value k.
OUPUT: node in BST whose key equals to k
1 if(x==NIL) OR (k==x.key)
2 　　return x
3 if(k<x.key)
4 　　return TREE-SEARCH(x.left, k)
5 else return TREE-SEARCH(x.right, k)

算法解释：当我们要找到key值为k的节点在BST中的位置，我们一般调用上述函数TREE-SEARCH(ROOT, k)（ROOT为BST的根节点）。如果ROOT节点的key值等于k，则我们要找的节点就是根节点ROOT。如果不是，根据BST的特殊性质：

left.key<parent.key<=right.key

我们比较当前节点的key值，如果current.key<k,则要在当前节点的左子树中查找，反之，则在右子树中查找。[line3-line5]

 

2.2 MINIMUM:

TREE-MINIMUM(x)
INPUT: BST ROOT node
OUTPUT: the smallest key in BST
1 if(x==NIL)  return;
2 while(x.left!=NIL)
3 　　x=x.left
4 return x.key

算法解释：一个BST的最左叶子节点的key值就是BST所有key值中最小的。这个根据BST的特殊性质很容易推导出来：

因为 left.key < parent.key < parent.key < .... < root.key

有了MINIMUM算法，MAXIMUM算法也就有了：

 

2.3 MAXIMUM:

TREE-MAXIMUM(x)
INPUT: BST ROOT node
OUTPUT: the smallest key in BST
1 if(x==NIL)  return;
2 while(x.right!=NIL)
3 　　x=x.right
4 return x.key

2.4 SUCCESSOR：

TREE-SUCCESSOR(x)
INPUT: arbitray node x in BST
OUTPUT: x's successor node
1 if(x.right!=NIL)
2 　　TREE-MINIMUM(x.right)
3 y=x.parent
4 while(y!=NIL AND y.left==x)
5 　　x=y
6　　 y=y.parent
7 return y

这里说明一下SUCCESSOR的含义，x的SUCCESSOR满足x.key<=x.SUCCESSOR.key,并且x.SUCCESSOR.key是距离x.key最近的值，即x.SUCCESSOR.key是x.key的最小上限（minimum ceiling）

算法思想：因为在BST中，有x.key<=x.right.key。所以如果某BST的节点x有右孩子节点(x.right!=NIL)，则利用TREE-MINIMUM在x的右子树中查找即可。如果x不存在右孩子，则检查x是否有父亲节点并且x必须是父亲节点的左孩子，只有这样才有parent.key>parent.left.key。但找到x的parent就结束了吗，还没有，就像TREE-MINIMUM函数一样，我们需要逐层查找，当找到符合条件的parent后，我们递归的继续检查parent节点有没有parent.parent节点符不符合上述条件。知道访问到的parent节点不符合该条件为止。

2.5 INSERT：

TREE-INSERT(T, z)
1 y=NIL
2 x=T.ROOT
3 while(x!=NIL) 
4　　 y=x
5 　　if(z.key<x.key)
6　　 　　x=x.left
7 　　else x=x.right
8 z.p=y
9 if(y==NIL) T.ROOT=z
10 if(z.key<y.key) y.left=z
11 else y.right=z

用一张图来解释该算法：

　　　

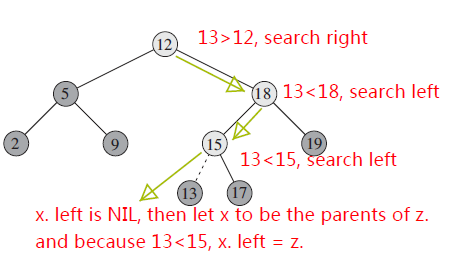
虚线指向的key值为13的节点是即将要插入BST的点，其他的点已经在BST上。可以看到从ROOT节点出发，根据“左小右大”规则，我们很快找到了key值为15的节点，因为13<15，所以检查‘15’节点是否有左孩子，结果是没有，所以把13放到15的左孩子节点处。我们可以想象如果要插入的节点key是16会怎么样？同样的，我们还是找到‘15’节点，但是16>15，所以继续往‘右’查找，找到‘17’，因为16<17,看17有没有左孩子节点，没有，所以会把‘16’放到‘17’的左孩子节点处。

2.6 TRANSPLANT：

TRANPLANT(T, u, v)
1 if (u.parent==NIL) T.ROOT=v
2 else if(u==u.parent;.left) u.parent.left=v
3 else u.parent.right=v
4 if(v!=NIL) v.parent=u.parent

 还是用一张图来展示比较清晰：

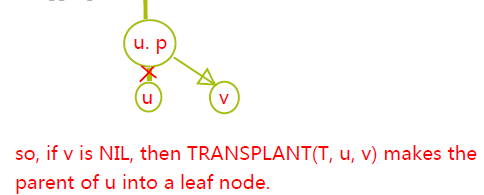
2.7 DELETE：

TREE-DELETE(T, z)
1 if z.left==NIL
2         TRANSPLANT(T, z, z.right)
3 else if z.right == NIL
4         TRANSPLANT(T, z, z.left)
5 else y=TREE-MINIMUM(z.right)
6         if y.parent!=z
7                 TRANSPLANT(T, y, y.right)    
8                  y.right=z.right
9                 y.right.parent=y
10       TRANSPLANT(T, z, y)
11       y.left=z.left
12       y.left.parent=y

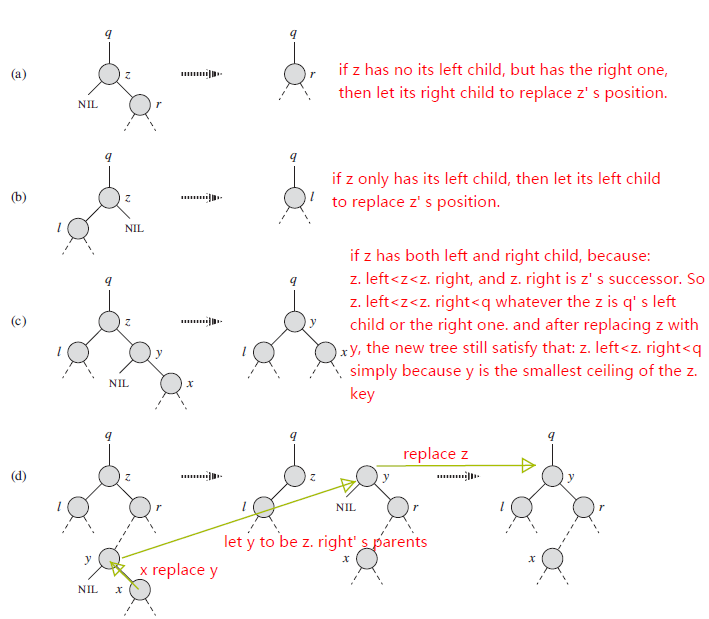
 DELETE算法相对来说比较麻烦一些，需要考虑的情况要多一些。因为要在删除BST的某一节点后仍能维持BST的基本性质。假设要删除的节点是z，z的key值为k。根据“左小右大”原则，z.left.key<k<=z.right.key.如果这时候吧z删了，谁来接替z的位置呢并且保证解体之后的新BST满足性质呢？方法我们可以根据性质来推导：我们要找到一个除了z以外的节点在BST中，该节点假设为P，那么P.key要大于z.left.key并且P.key>=z.right.key，实际上很明显的，唯一符合要求的就是z的SUCCESSOR。

如果z只有左子树或者只有右子树，那么问题就很简单，使z的左孩子或者右孩子来顶替z的位置即可。如果z的左子树和右子树都存在，那么问题稍微复杂一点，我们要在BST上找到z的SUCCESSOR。如此一来，这个问题又变成我们之前讨论的SUCCESSOR问题了，总共有两种情形：

第一种情形：z的右孩子就是我们要找的z的SUCCESSOR，那我们就直接TRANSPLANT移植以z.right为根的子树到z的位置中去。

第二种情形：z的右孩子不是我们要找的z的SUCCESSOR，那我们就从z.right出发，‘深入’寻找知道找到z的SUCCESSOR，假设为Q。

那么我们让Q成为z.right的父亲节点，并且让以Q为根的右子树（因为是根据“最左原则”找到的Q，Q要么是以z.right为根的left-most叶子节点，要么Q只有右子树。）取代Q的位置。最后让Q取代z的位置。。。很绕。。。还是见图吧。