CF446C DZY Loves Fibonacci Numbers

CF446C DZY Loves Fibonacci Numbers

洛谷评测传送门

题目描述

In mathematical terms, the sequence F_{n}F**n of Fibonacci numbers is defined by the recurrence relation

F_{1}=1; F_{2}=1; F_{n}=F_{n-1}+F_{n-2} (n>2). DZY loves Fibonacci numbers very much. Today DZY gives you an array consisting of nn integers: a_{1},a_{2},...,a_{n}a1,a2,...,a**n . Moreover, there are mm queries, each query has one of the two types:

1. Format of the query " 1 l r1 l r ". In reply to the query, you need to add F_{i-l+1}F**i−l+1 to each element a_{i}a**i , where l<=i<=rl<=i<=r .
2. Format of the query " 2 l r2 l r ". In reply to the query you should output the value of 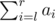modulo 1000000009 (10^{9}+9) .

Help DZY reply to all the queries.

输入格式

The first line of the input contains two integers nn and mm ( 1<=n,m<=3000001<=n,m<=300000 ). The second line contains nn integers a_{1},a_{2},...,a_{n} (1<=a_{i}<=10^{9}) — initial array aa .

Then, mm lines follow. A single line describes a single query in the format given in the statement. It is guaranteed that for each query inequality 1<=l<=r<=n1<=l<=r<=n holds.

输出格式

For each query of the second type, print the value of the sum on a single line.

题意翻译

题面大意：给出一个数列，每次可以选取一个区间，按顺序加上第i个Fibonacci Numbers(斐波那契数)进行更新，也可以查询某一个区间的总和。

感谢@char32_t 提供的翻译

输入输出样例

输入 #1复制

输出 #1复制

说明/提示

After the first query, a=[2,3,5,7]a=[2,3,5,7] .

For the second query, sum=2+3+5+7=17sum=2+3+5+7=17 .

After the third query, a=[2,4,6,9]a=[2,4,6,9] .

For the fourth query, sum=2+4+6=12sum=2+4+6=12 .

题解：

2019.11.5模拟赛T3 40分场

(O(n^2))的做法能水10分，普通线段树毫无优化能跑30分。感谢出题人@littleseven

一看是黑题顿时毫无思路。因为这道题涉及到的知识点：线段树+(Fibonacci)数列是联赛范围内，所以它就这样被收进了联赛模拟赛中。

介绍一下正解：

首先我们能想到，区间修改区间查询一定需要线段树。而且这道题难住我们的点就是如何维护修改操作，换句话说，如何进行下传标记。

但是我们稍微动动脑能发现这个性质：（我在考场上也推出来了）

对于一个要修改的区间([l,r])中的第(x)项，它需要加上这一项：(fib_{x-l+1})。(fib)表示斐波那契数列。

而斐波那契数列有这样的性质：（很重要，虽然蒟蒻也是做了这道题才知道）

[fib[n+m]=fib[n+1]fib[m]+fib[n]fib[m-1] ]

那么对于这个位置(x)，设(n=-l,m=x+1)，它加上了：

[fib[x-l+1]=fib[1-l]fib[x+1]+fib[x]fib[-l] ]

那么对于线段树上的节点，我们需要维护两个标记：(add1[i],add2[i])，分别统计对于一个区间为([l,r])的节点，(add1(fib_{l+1}+fib_{l+2}+cdots+fib_{r+1}))，(add2(fib_{l}+fib_{l+1}+cdots+fib_{r}))。

修改的时候，给(add1)加上(fib_{-l+1})，给(add2)加上(fib_{-l})，然后进行线段树的正常(pushdown)操作即可。

代码：

#include<cstdio>
#define lson pos<<1
#define rson pos<<1|1
using namespace std;
const int maxn=3*1e5+10;
const int mod=1e9+9;
char *p1,*p2,buf[100000];
#define nc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++)
int read()
{
    int x=0,f=1;
    char ch=nc();
    while(ch<48){if(ch=='-')f=-1;ch=nc();}
    while(ch>47)    x=(((x<<2)+x)<<1)+ch-48,ch=nc();
    return x*f;
}
int n,m;
int a[maxn],sum[maxn],fib[maxn],ffib[maxn];
int tree[maxn<<2],add1[maxn<<2],add2[maxn<<2];
void fibonacci()
{
    fib[1]=fib[2]=sum[1]=ffib[1]=1;
    sum[2]=2;
    ffib[2]=mod-1;
    for(int i=3;i<=n+1;i++)
    {
        fib[i]=(fib[i-1]+fib[i-2])%mod;
        sum[i]=(sum[i-1]+fib[i])%mod;
        ffib[i]=(i&1)?fib[i]:mod-fib[i];
    }
}
void build(int pos,int l,int r)
{
    int mid=(l+r)>>1;
    if(l==r)
    {
        tree[pos]=a[l]%mod;
        return;
    }
    build(lson,l,mid);
    build(rson,mid+1,r);
    tree[pos]=(tree[lson]+tree[rson])%mod;
}
void mark(int pos,int l,int r,int a1,int a2)
{
    add1[pos]=(add1[pos]+a1)%mod;
    add2[pos]=(add2[pos]+a2)%mod;
    tree[pos]=(tree[pos]+1ll*(sum[r+1]-sum[l]+mod)%mod*a1%mod)%mod;
    tree[pos]=(tree[pos]+1ll*(sum[r]-sum[l-1]+mod)%mod*a2%mod)%mod;
}
void pushdown(int pos,int l,int r)
{
    int mid=(l+r)>>1;
    mark(lson,l,mid,add1[pos],add2[pos]);
    mark(rson,mid+1,r,add1[pos],add2[pos]);
    add1[pos]=add2[pos]=0;
}
void update(int pos,int l,int r,int x,int y,int a1,int a2)
{
    int mid=(l+r)>>1;
    if(x<=l && r<=y)
    {
        mark(pos,l,r,a1,a2);
        return;
    }
    pushdown(pos,l,r);
    if(x<=mid)
        update(lson,l,mid,x,y,a1,a2);
    if(y>mid)
        update(rson,mid+1,r,x,y,a1,a2);
    tree[pos]=(tree[lson]+tree[rson])%mod;
}
int query(int pos,int l,int r,int x,int y)
{
    int ret=0;
    int mid=(l+r)>>1;
    if(x<=l && r<=y)
        return tree[pos]%mod;
    pushdown(pos,l,r);
    if(x<=mid)
        ret=(ret+query(lson,l,mid,x,y))%mod;
    if(y>mid)
        ret=(ret+query(rson,mid+1,r,x,y))%mod;
    return ret%mod;
}
int main()
{
    n=read();m=read();
    for(int i=1;i<=n;i++)
        a[i]=read();
    fibonacci();
    build(1,1,n);
    for(int i=1;i<=m;i++)
    {
        int opt,l,r;
        opt=read();l=read();r=read();
        if(opt==1)
            update(1,1,n,l,r,ffib[l-1],ffib[l]);
        else
            printf("%d
",query(1,1,n,l,r));
    }
    return 0;
}