前边讨论了我们介绍了成长函数和break point,现在继续讨论m是否成长很慢,是否能够取代M。

成长函数就是二分类的排列组合的数量。break point是第一个不能shatter(覆盖所有情形)的点。
1.break point对成长函数的限制
我们希望

这里引入上限函数 bound function:给了break point,看看可以组成多少排列组合,下面证明boundfunction是多项式成长的。
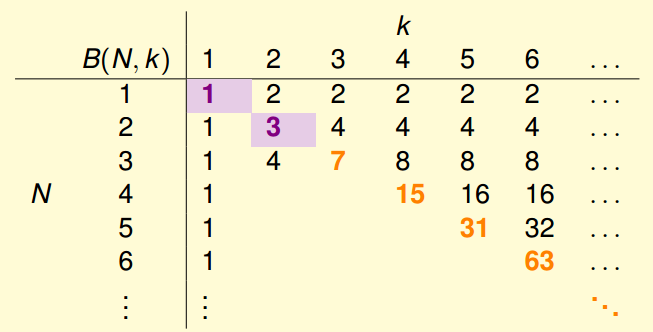
右上角相当于没有加条件限制,对角线就是全部的减1嘛,因为全部不可能,小一点,找个上限。
接下来填剩余部分,通过转换得到B(4, 3) = B(3, 3) + B(3,2)


所以得到,
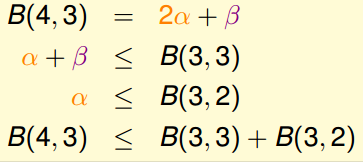
同理得到,

由数学归纳法可以证明:
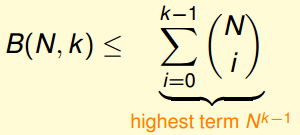
所以,我们就得到:成长函数会被上限函数bound住,上限函数会被上限函数的上限函数bound住,上限函数的上限会被一个与break point有关的多项式bound住。

接下来,我们回到最之前的Hoeffding不等式转换式:

接下来证明它们。
由于Eout是无限个点的,因此我们不能直接带入上限,现在想办法转化,类似于交叉验证,现在选择一个Ein',那么有,



所以,最终我们得到,

对于PLA来说,由于我们知道4是一个break point,所以最终成长函数会被限制住,也就是learning是可以的。
下一节引入VC Bound继续解释为什么机器可以学习。http://www.cnblogs.com/futurehau/p/6260332.html