12.石子合并 区间DP

 

 区间dp问题是在定义状态时，定义了一个区间

区间dp的状态表示一般是dp[i][j]，表示从i到j这个区间，也就是从第i堆石子到第j堆石子这个区间

以最后一次合并的分界线的位置，来进行集合的划分

假设从i到j一共有k个，k = j - i + 1

按照左右两堆左边有几个来划分，左边有1个，2个，...，k - 1个

比如最后的两堆左边是[i, k]，右边是[k + 1, j]

还是先减去最后一步，再求最值，再加上最后一步

dp[i][k] + dp[k + 1][j]                           +     s[j] - s[i - 1]

左边的最小代价 + 右边的最小代价　　　　最后一步的最小代价

除了最后一步的最小代价　　　　　　　　从第i堆到第j堆石子的总重量（前缀和）

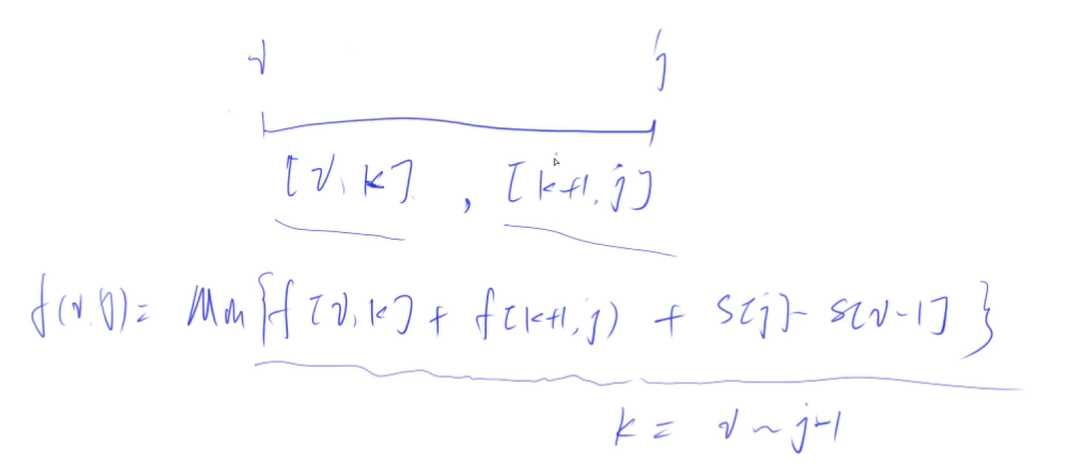
 时间复杂度：

状态数量：两维n * n  

状态计算：需要枚举k，k是O(n)的计算量

所以一共是n ^ 3

区间dp问题我们要保证在算每个dp[i][j]时，dp[i][j]用到的所有状态都已经计算好了

所以循环时有一个顺序

我们按照区间长度从小到大来做，区间长度从1开始，这样就可以保证我们在算某个状态时，这个状态所依赖的所有状态都是已经算好了的

#include <bits/stdc++.h>
using namespace std;
const int N = 310;
int s[N]; //存储前缀和
int dp[N][N];
int main() {
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> s[i];
        s[i] += s[i - 1];
    }
    //区间长度为1时，不需要合并，代价是0
    for (int len = 2; len <= n; len++) { //按照长度从小到大枚举所有状态
        for (int i = 1; len <= n - i + 1; i++) { //枚举起点
            //cout << "len: " << len << " i: " << i << endl;
            int l = i, r = i + len - 1; //区间的左右端点, len = r - l + 1的变形
            //cout << "len: " << len << " l: " << l << " r: " << r << endl;
            dp[l][r] = 1e9; //算最小值，需要初始化为一个较大的数
            for (int k = l; k < r; k++) { //枚举分界点，从i到j - 1
                dp[l][r] = min(dp[l][r], dp[l][k] + dp[k + 1][r] + s[r] - s[l - 1]);   
            }
        }
    }
    cout << dp[1][n] << endl; //dp[1][n]就是答案
    return 0;
}