样例解释：用方块表示牛
题目意思就是，我们要安排一个从上到下的顺序，使得牛按照这个顺序叠高高
然后使得所有牛的危险系数的最大值最小
每个牛的危险系数 = 它上面所有牛的重量w之和 减去 它自己的强壮值s
证明：
首先有
成立
然后需要证明
，用反证法：假设最优解不是按照wi + si从小到大排序的
那么一定存在相邻两头牛，使得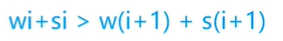
然后如果我们交换这两头牛的话，看看会有什么影响
首先，交换这两头牛的话，对除了这两头牛的其他牛没有影响
在都去掉
后，每个数再加上一个si和一个s(i + 1)
首先wi + si一定大于si，然后根据我们假设的条件，又有wi + si > w(i + 1) + s(i + 1)
因此si 和 w(i + 1) + s(i + 1)中的最大值一定小于 wi + si
也就是si 和 w(i + 1) + s(i + 1)中的最大值一定小于 s(i + 1) 和 wi + si中的最大值
所以只要有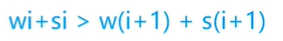的情况出现，交换完后，这两个数的最大值一定会变小
因为是要求牛的最大值的最小值，所以根据反证，推出矛盾，最优解不是按照wi + si从小到大排序的，答案不是最优的
1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef pair<int, int> PII; 4 const int N = 50010; 5 PII cow[N]; 6 int main() { 7 int n; 8 cin >> n; 9 for (int i = 0; i < n; i++) { 10 int w, s; 11 cin >> w >> s; 12 cow[i] = {w + s, s}; 13 } 14 sort(cow, cow + n); 15 int res = -2e9, sum = 0; 16 //先把最小值取为-INF 17 //sum是每头牛上面的牛重量之和 18 for (int i = 0; i < n; i++) { 19 int s = cow[i].second, w = cow[i].first - s; 20 res = max(res, sum - s); 21 sum += w; 22 } 23 cout << res << endl; 24 return 0; 25 }