最大的和

 

 

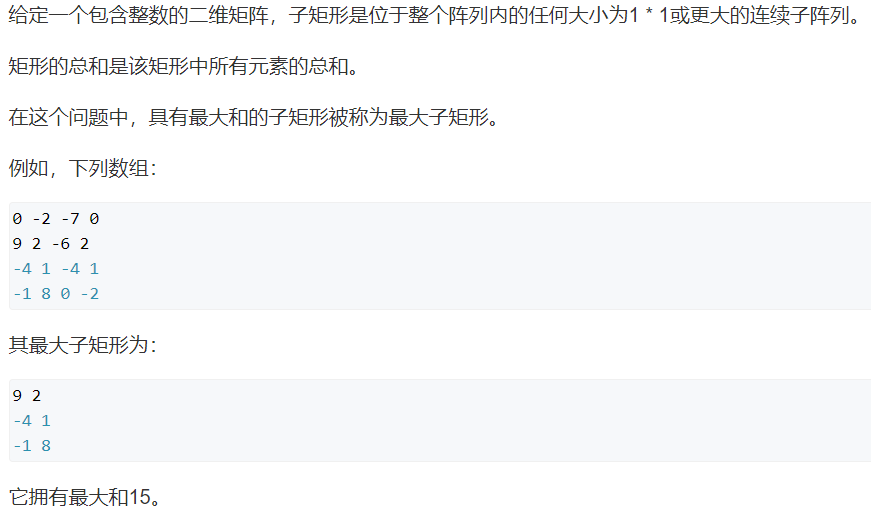
 解析转载自https://www.acwing.com/solution/content/4127/

=====转载开始=====

左上角和右下角两个点可以确定一个矩形。枚举这两个点要用4个for循环 如果用二维前缀和，那么这个做法的复杂度的就是O(n^4)。

其实这个方案可以优化，那就是不枚举点。

 

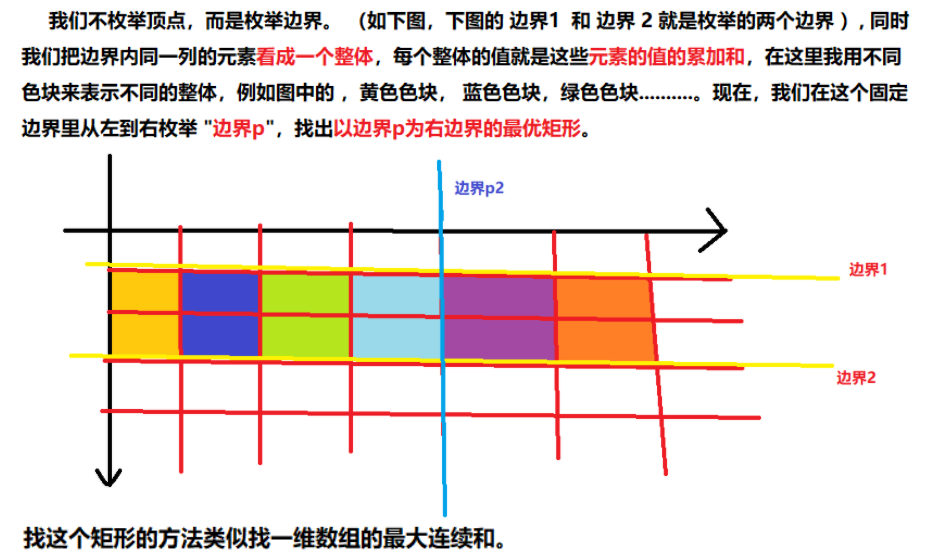
所以我们可以利用前缀和数组表示出每个色块表示的值，然后做类似找一维数组最大连续和的操作。这样来枚举出最优矩形。

枚举边界要用3个for，复杂度为 O（n^3)

=====转载结束=====

#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int a[N][N];
int main() {
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            cin >> a[i][j];
            a[i][j] += a[i - 1][j]; //同一列的前缀和
        }
    }
    int res = -2e9;
    for (int i = 1; i <= n; i++) { //枚举边界1
        for (int j = i; j <= n; j++) { //枚举边界2
            int last = 0;
            for (int k = 1; k <= n; k++) { //枚举边界
                //last是前面数字的最大和如果小于0 舍弃
                last = max(last, 0) + a[j][k] - a[i - 1][k]; 
                res = max(res, last);
            }
        }
    }
    cout << res << endl;
    return 0;
}