Andrew Ng机器学习课程笔记(一)之线性回归
版权声明:本文为博主原创文章,转载请指明转载地址
http://www.cnblogs.com/fydeblog/p/7364598.html
前言
学习了Andrew Ng课程,开始写了一些笔记,现在写完第5章了,先把这5章的内容放在博客中,后面的内容会陆续更新!
这篇博客主要记录了Andrew Ng课程第一章线性回归,主要介绍了梯度下降法,正规方程,损失函数,特征缩放,学习率的选择等等
1.梯度下降法
原理图解:
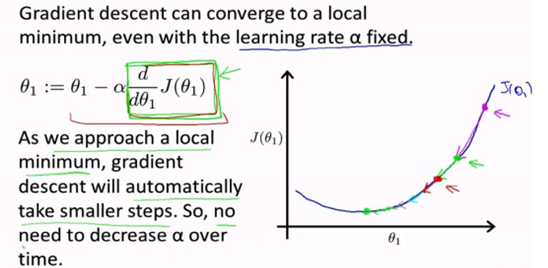
(1) 目标:最小化建立代价函数
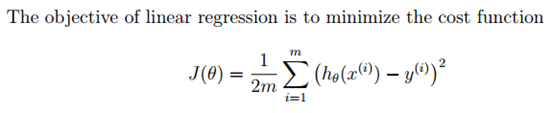
Tips: J(θ)可以向量化进行计算,更加简单而且计算方便

(2) 梯度下降法的参数更新
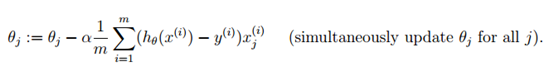
(3) 注意事项与实用技巧
①多变量线性回归,每个变量要进行特征缩放到相同范围

②画绘制迭代次数和代价函数的图表来观测算法在何时趋于收敛
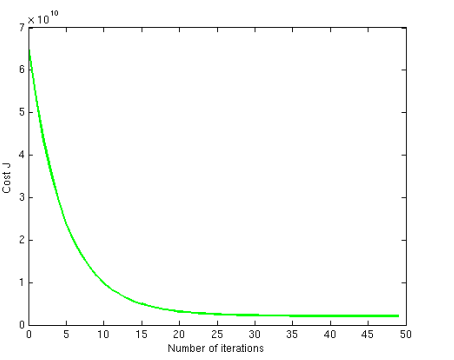
③学习率的选择
梯度下降算法的每次迭代受到学习率的影响,如果学习率α过小,则达到收敛所需的迭代次数会非常高;如果学习率α过大,每次迭代可能不会减小代价函数,可能会越过局部最小值导致无法收敛。
通常可以考虑尝试些学习率:α=0.01, 0.03, 0.1, 0.3, 1, 3, 10
2. 正规方程
上面使用梯度下降算法,但是对于某些线性回归问题,正规方程方法是更好的解决方案。

在Octave或matlab中,正规方程写作:
pinv(X'*X)*X'*y
注:对于那些不可逆的矩阵(通常是因为特征之间不独立,如同时包含英尺为单位的尺寸和米为单位的尺寸两个特征,也有可能是特征数量大于训练集的数量),正规方程方法是不能用的。
3. 梯度下降法与正规方程比较
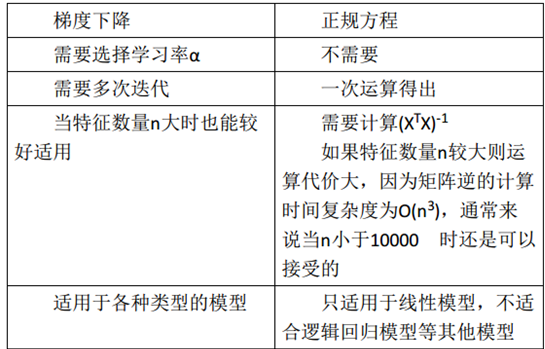
总结一下,只要特征变量的数目并不大,标准方程是一个很好的计算参数θ的替代方法。具体地说,只要特征变量数量小于一万,通常使用标准方程法,而不使用梯度下降法。