题目链接:
https://www.lydsy.com/JudgeOnline/problem.php?id=1202
题目大意:
刁姹接到一个任务,为税务部门调查一位商人的账本,看看账本是不是伪造的。账本上记录了n个月以来的收入情况,其中第i 个月的收入额为Ai(i=1,2,3...n-1,n), 。当 Ai大于0时表示这个月盈利Ai 元,当 Ai小于0时表示这个月亏损Ai 元。所谓一段时间内的总收入,就是这段时间内每个月的收入额的总和。 刁姹的任务是秘密进行的,为了调查商人的账本,她只好跑到商人那里打工。她趁商人不在时去偷看账本,可是她无法将账本偷出来,每次偷看账本时她都只能看某段时间内账本上记录的收入情况,并且她只能记住这段时间内的总收入。 现在,刁姹总共偷看了m次账本,当然也就记住了m段时间内的总收入,你的任务是根据记住的这些信息来判断账本是不是假的。
思路:
一:差分约束系统转化
对于一段区间的和,可以转化成前缀和相减的形式。
比如区间a-b的和为c,也就是sum[b] - sum[a - 1] = c
可以写成两个式子:
sum[b] - sum[a - 1] <= c
sum[b] - sum[a - 1] >= c
根据差分约束系统式子: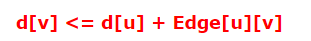
也就是a-1到b 权值为c
b到a-1 权值为-c
判断有没有负环,有的话无解,输出false。
二、带权并查集:
也是转化成前缀和的形式。对于每个节点所带的权值cnt[i] = s[root] - s[i]
1、如果x=a-1,y=b在同一子树中,cnt[x] = s[root] - s[x] cnt[y] = s[root] - s[y]
那么cnt[x] - cnt[y] = s[y] - s[x]判断是否等于输入值c。
2、不在同一子树,进行合并。
设fx为x子树根节点 fy为y子树根节点。
有cnt[x] = s[fx] - s[x] cnt[y] = s[fy] = s[y] 目前又给出条件:s[y] - s[x] = z;
将fy并入fx中,那么cnt[fy]应该设置成s[fx] - s[fy]
由上述三个式子可得:cnt[fy]应该设置成cnt[x] - cnt[y] - z
这样带权并查集的合并就写好了。
差分:
1 #include<bits/stdc++.h> 2 #define IOS ios::sync_with_stdio(false);//不可再使用scanf printf 3 #define Max(a, b) ((a) > (b) ? (a) : (b))//禁用于函数,会超时 4 #define Min(a, b) ((a) < (b) ? (a) : (b)) 5 #define Mem(a) memset(a, 0, sizeof(a)) 6 #define Dis(x, y, x1, y1) ((x - x1) * (x - x1) + (y - y1) * (y - y1)) 7 #define MID(l, r) ((l) + ((r) - (l)) / 2) 8 #define lson ((o)<<1) 9 #define rson ((o)<<1|1) 10 #define Accepted 0 11 #pragma comment(linker, "/STACK:102400000,102400000")//栈外挂 12 using namespace std; 13 inline int read() 14 { 15 int x=0,f=1;char ch=getchar(); 16 while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();} 17 while (ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} 18 return x*f; 19 } 20 21 typedef long long ll; 22 const int maxn = 2000 + 10; 23 const int MOD = 1000000007;//const引用更快,宏定义也更快 24 const int INF = 1e9 + 7; 25 const double eps = 1e-6; 26 27 struct edge 28 { 29 int v, w; 30 edge(){} 31 edge(int v, int w):v(v), w(w){} 32 }; 33 vector<edge>e; 34 vector<int>G[maxn]; 35 bool inq[maxn];//是否在队列中 36 int d[maxn]; 37 int cnt[maxn];//入队次数 38 int n, m; 39 void addedge(int u, int v, int w) 40 { 41 e.push_back(edge(v, w)); 42 G[u].push_back(e.size() - 1); 43 } 44 bool SPFA() 45 { 46 queue<int>q; 47 memset(inq, 0, sizeof(inq)); 48 memset(cnt, 0, sizeof(cnt)); 49 for(int i = 0; i <= n; i++){d[i] = 0; inq[0] = true;q.push(i);} 50 while(!q.empty()) 51 { 52 int u = q.front(); 53 q.pop(); 54 inq[u] = 0; 55 for(int i = 0; i < G[u].size(); i++) 56 { 57 int v = e[G[u][i]].v; 58 int w = e[G[u][i]].w; 59 if(d[v] > d[u] + w) 60 { 61 d[v] = d[u] + w; 62 if(!inq[v]) 63 { 64 q.push(v); 65 inq[v] = 1; 66 if(++cnt[v] > n)return true; 67 } 68 } 69 } 70 } 71 return false; 72 } 73 int main() 74 { 75 int T; 76 scanf("%d", &T); 77 while(T--) 78 { 79 scanf("%d%d", &n, &m); 80 for(int i = 0; i <= n; i++)G[i].clear(); 81 e.clear(); 82 int u, v, w; 83 for(int i = 1; i <= m; i++) 84 { 85 scanf("%d%d%d", &u, &v, &w); 86 u--; 87 addedge(u, v, w); 88 addedge(v, u, -w); 89 } 90 if(SPFA())puts("false"); 91 else puts("true"); 92 } 93 return Accepted; 94 }
带权并查集:
1 #include<bits/stdc++.h> 2 #define IOS ios::sync_with_stdio(false);//不可再使用scanf printf 3 #define Max(a, b) ((a) > (b) ? (a) : (b))//禁用于函数,会超时 4 #define Min(a, b) ((a) < (b) ? (a) : (b)) 5 #define Mem(a) memset(a, 0, sizeof(a)) 6 #define Dis(x, y, x1, y1) ((x - x1) * (x - x1) + (y - y1) * (y - y1)) 7 #define MID(l, r) ((l) + ((r) - (l)) / 2) 8 #define lson ((o)<<1) 9 #define rson ((o)<<1|1) 10 #define Accepted 0 11 #pragma comment(linker, "/STACK:102400000,102400000")//栈外挂 12 using namespace std; 13 inline int read() 14 { 15 int x=0,f=1;char ch=getchar(); 16 while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();} 17 while (ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} 18 return x*f; 19 } 20 21 typedef long long ll; 22 const int maxn = 2000 + 10; 23 const int MOD = 1000000007;//const引用更快,宏定义也更快 24 const int INF = 1e9 + 7; 25 const double eps = 1e-6; 26 27 int cnt[maxn];//cnt[i]表示s[root] - s[i] 28 int p[maxn]; 29 int Find(int x) 30 { 31 if(x == p[x])return x; 32 int tmp = Find(p[x]);//此处不可以先路径压缩,需要更新x之后再进行路径压缩 33 cnt[x] += cnt[p[x]];//一开始 cnt[x] = s[p[x]] - s[x] cnt[p[x]] = s[root] - s[p[x]] 34 p[x] = tmp; //需要路径压缩转化成 cnt[x] = s[root] - s[x] 35 return p[x]; 36 } 37 int main() 38 { 39 int T; 40 scanf("%d", &T); 41 while(T--) 42 { 43 int n, m; 44 scanf("%d%d", &n, &m); 45 for(int i = 0; i <= n; i++)p[i] = i, cnt[i] = 0; 46 int flag = 0; 47 for(int i = 1; i <= m; i++) 48 { 49 int x, y, z; 50 scanf("%d%d%d", &x, &y, &z); 51 x--; 52 int fx = Find(x), fy = Find(y); 53 if(fx != fy) 54 { 55 //目前已知 s[y] - s[x] = z cnt[x] = s[fx] - s[x] cnt[y] = s[fy] - s[y] 56 //将y的根fy并入x的根fx中 那么需要设置cnt[fy] = s[fx] - s[fy] 57 //所以cnt[fy] = s[fx] - s[fy] = s[x] + cnt[x] - (s[y] + cnt[y]) = cnt[x] - cnt[y] - z 58 cnt[fy] = cnt[x] - cnt[y] - z; 59 p[fy] = fx; 60 } 61 else if(cnt[x] - cnt[y] != z)//验证s[y] - s[x] == z 等价于验证 cnt[x] - cnt[y] == z 62 { 63 flag = 1; 64 } 65 } 66 if(flag)puts("false"); 67 else puts("true"); 68 } 69 return Accepted; 70 }