网上看了几篇博客,还有OI Wiki,觉得整合度不够,于是特意写了篇博客。
参考资料
全网最!详!细!Tarjan算法讲解。
强连通分量(SCC)与缩点
强连通分量 - OI Wiki
正文
在学习强连通分量和缩点之前,请务必理解邻接表。
以下有OI Wiki的内容,有大佬博客里的内容,也有我自己的内容。
强连通分量
引入
强连通的定义是:有向图 G 强连通是指,G 中任意两个结点连通。
强连通分量(Strongly Connected Components,简称SCC)的定义是:极大的强连通子图。
举一个简单的例子。下面是一个有向图。
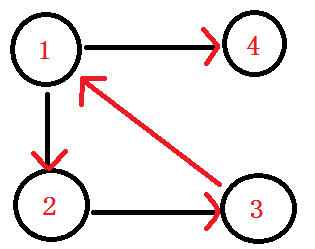
在这个图中, 1和2互相有路径可以到达对方,所以这两个点强连通;
1、2和3中任意两个点都连通,它们是这整个有向图的强连通分量。
求强连通分量。
下面我们介绍使用Tarjan算法求强连通分量。
我们举个例子说明这个算法是怎么运作的。图片取自《算法竞赛进阶指南》。
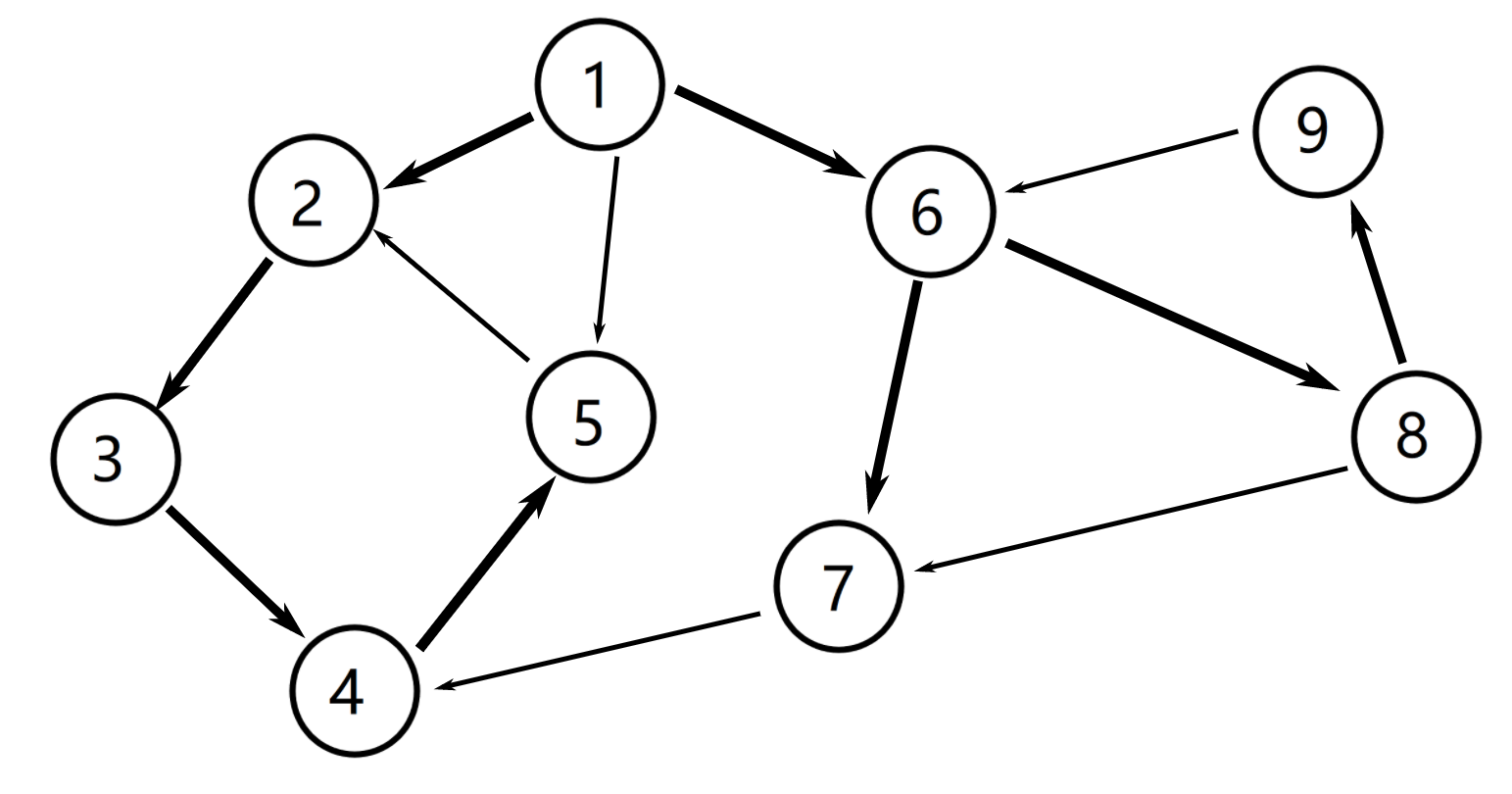
从 (①) 进入,dfn[1] = low[1] = ++index == 1
入栈 (①),此时的栈中元素为 (①),vis[1] = true,即点 (①) 在栈中。
往下找到 (②),dfn[2] = low[2] = ++index == 2
入栈 (②),此时栈中元素为 (①②),vis[2] = true
继续往下找到 (③),dfn[3] = low[3] = ++index == 3
入栈 (③),此时栈中元素为 (①②③),vis[3] = true
继续往下找到 (④),dfn[4] = low[4] = ++index == 4
入栈 (④),此时栈中元素为 (①②③④),vis[4] = true
继续往下找到 (⑤),dfn[5] = low[5] = ++index == 5
入栈 (5),此时栈中元素为 (①②③④⑤),vis[5] = true
继续往下找到 (②) 他太爷爷,dfn[2]被访问过并且还在栈中,说明这个 (②) 还在这个强连通分量中,值得发现。low[5] = min(low[5], dfn[2])
确定关系:(⑤) 节点比 (②) 节点出现得晚,即low[5] > dfn[2],所以 (⑤) 是 (①) 的子节点;low[5] = 2

然后发现 (⑤) 这个点没有出边了,返回到 (④) 这个点。
于是low[4] = min(low[4], low[5]) = 2
(④) 这个点也没有出边了,返回到 (③) 这个点。
于是low[3] = min(low[3], low[4]) = 2
(③) 这个点也没有出边了,返回到 (②) 这个点。
于是low[2] = min(low[2], low[2]) = 2,对没错,还是2
(②) 也没有出边,但是这时我们会发现low[2] == dfn[2] == 2,这就是说,点 (②) 是这个强连通分量的根,于是sccnt++(sccnt:强连通分量的个数),一直弹出栈顶元素,并把栈顶元素的颜色标记为sccnt(color[2] = sccnt),直到栈顶元素为2时最后弹出一次并标记颜色。此时栈中元素为 (①),vis[5] = vis[4] = vis[3] = vis[2] = false。
返回到 (①)。因为 (①) 比 (②) 出现得早,即low[1] < low[2],所以low[1]的值没变,还是1
点 (①) 还有出边,继续往下找到 (⑤)。嗯?dfn[5]已经有一个值5了,再看vis[5] == true,说明 (⑤) 这个点还在栈中,所以low[1] = min(low[1], dfn[5]) = 1(因为low[1] == 1,dfn[5] == 2)
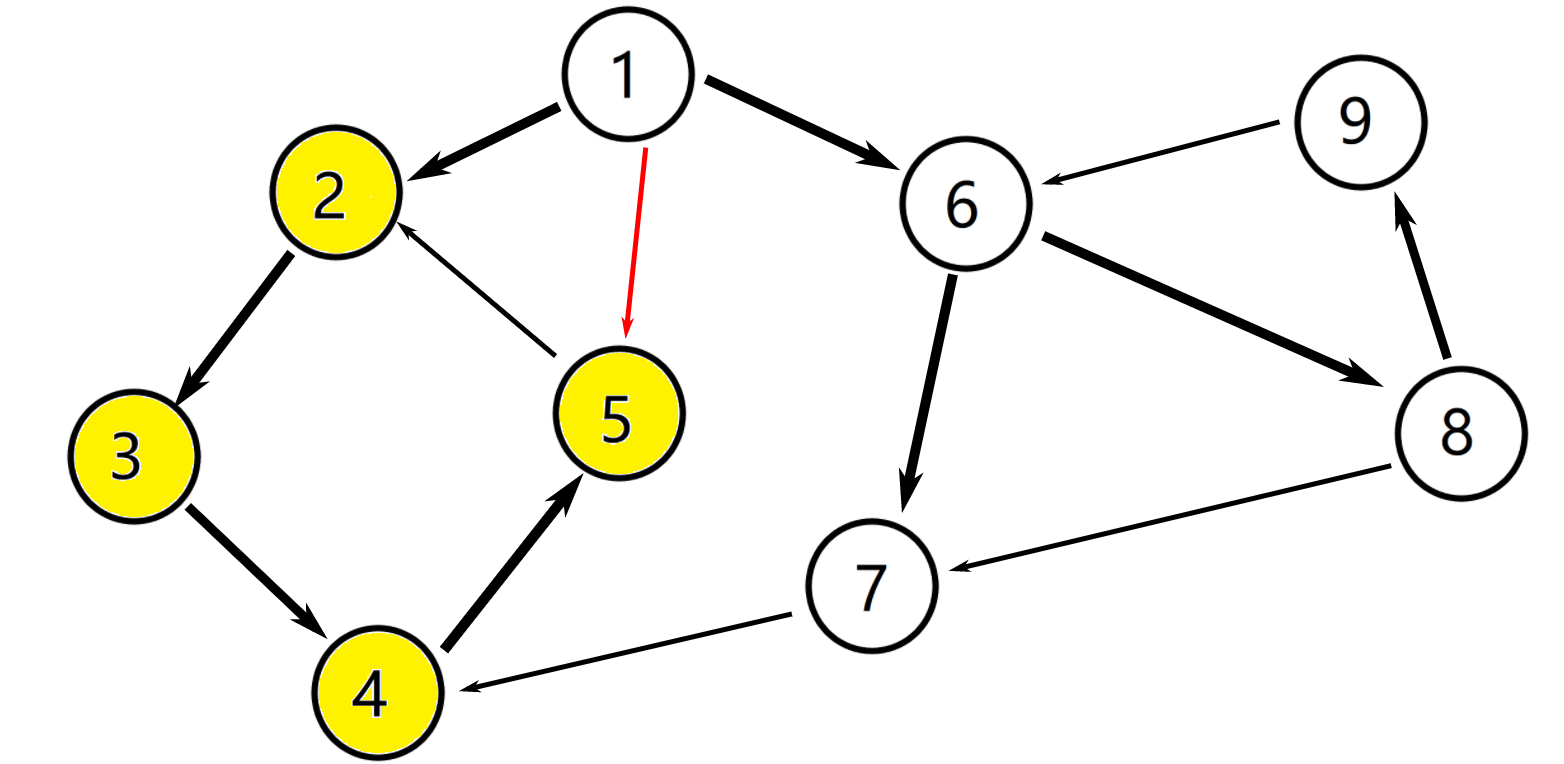
唉,现在同学都在准备省选,要不是我去年NOIP第一题用了邻接矩阵,数组开得太大了,我也去参加省选了(看出我有多蒻了吧)
点 (①) 还有出边,继续往下找找到 (⑥),dfn[6] = low[6] = ++index == 6
入栈 (⑥),此时栈中元素为 (①⑥) ,vis[6] = true
继续往下找到 (⑦),dfn[7] = low[7] = ++index = 7
入栈 (⑦),此时栈中元素为 (①⑥⑦),vis[7] = true
继续往下找到 (④),发现dfn[4] == 4,说明 (④) 已经被访问过了,又因为vis[4] == false,也就是 (④) 不在栈中,就不用管它。
(⑦) 没有别的出边了。判断此时dfn[7] == low[7] == 7,所以 (⑦) 是一个强连通分量的根。于是:Ⅰ:sccnt++;Ⅱ:把栈顶元素(即 (⑦) 的颜色标记为sccnt),将其弹出。此时栈中元素为 (①⑥)。
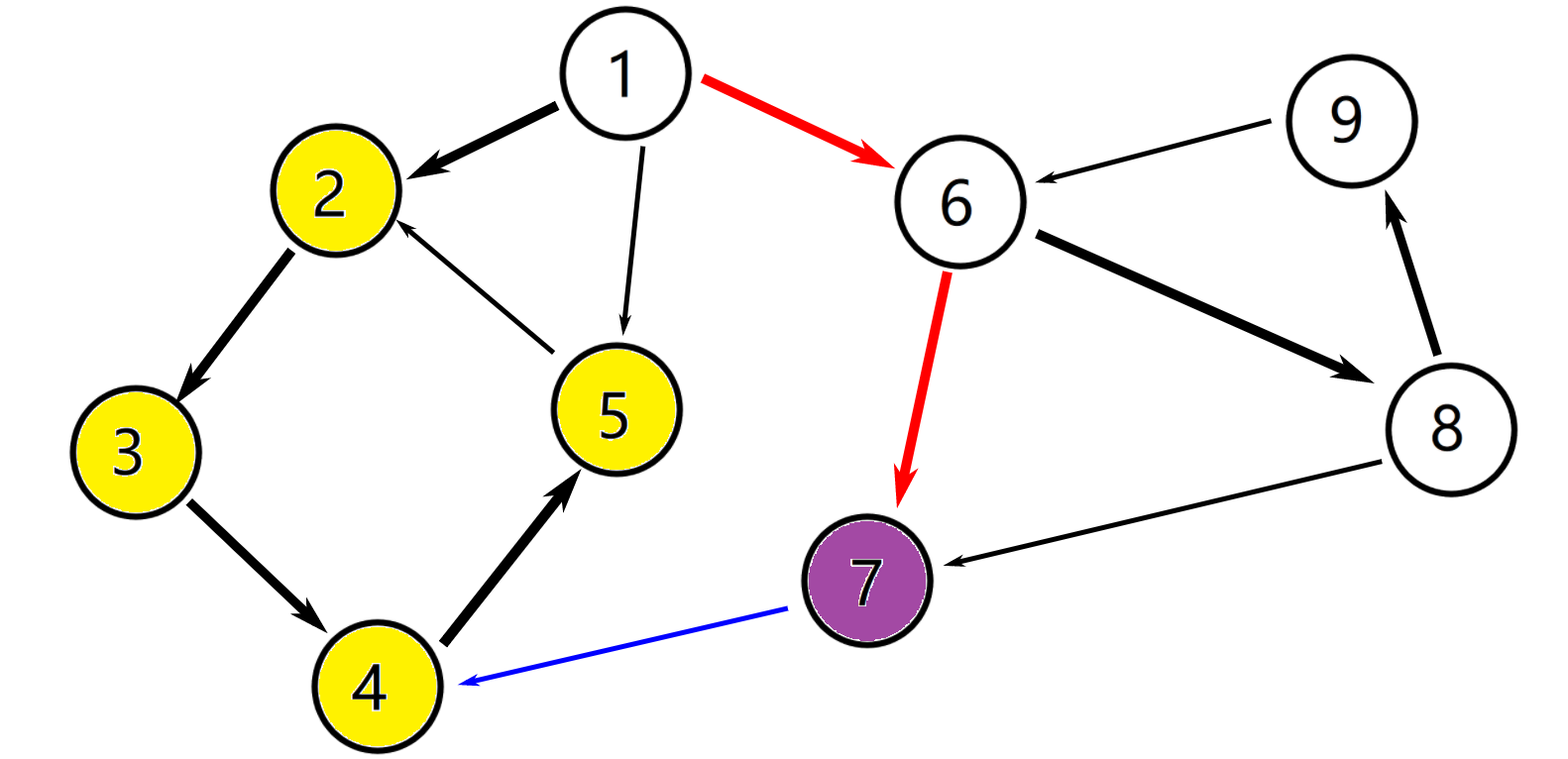
返回到 (⑥),找到点 (⑧),dfn[8] = low[8] = ++index = 8
入栈 (⑧),此时栈中元素为 (①⑥⑧),vis[8] = true
往下找到 (⑦),发现dfn[7] == 7,说明 (⑦) 已经被访问过了,又因为vis[7] ==false,(⑦) 不在栈中,不用管。
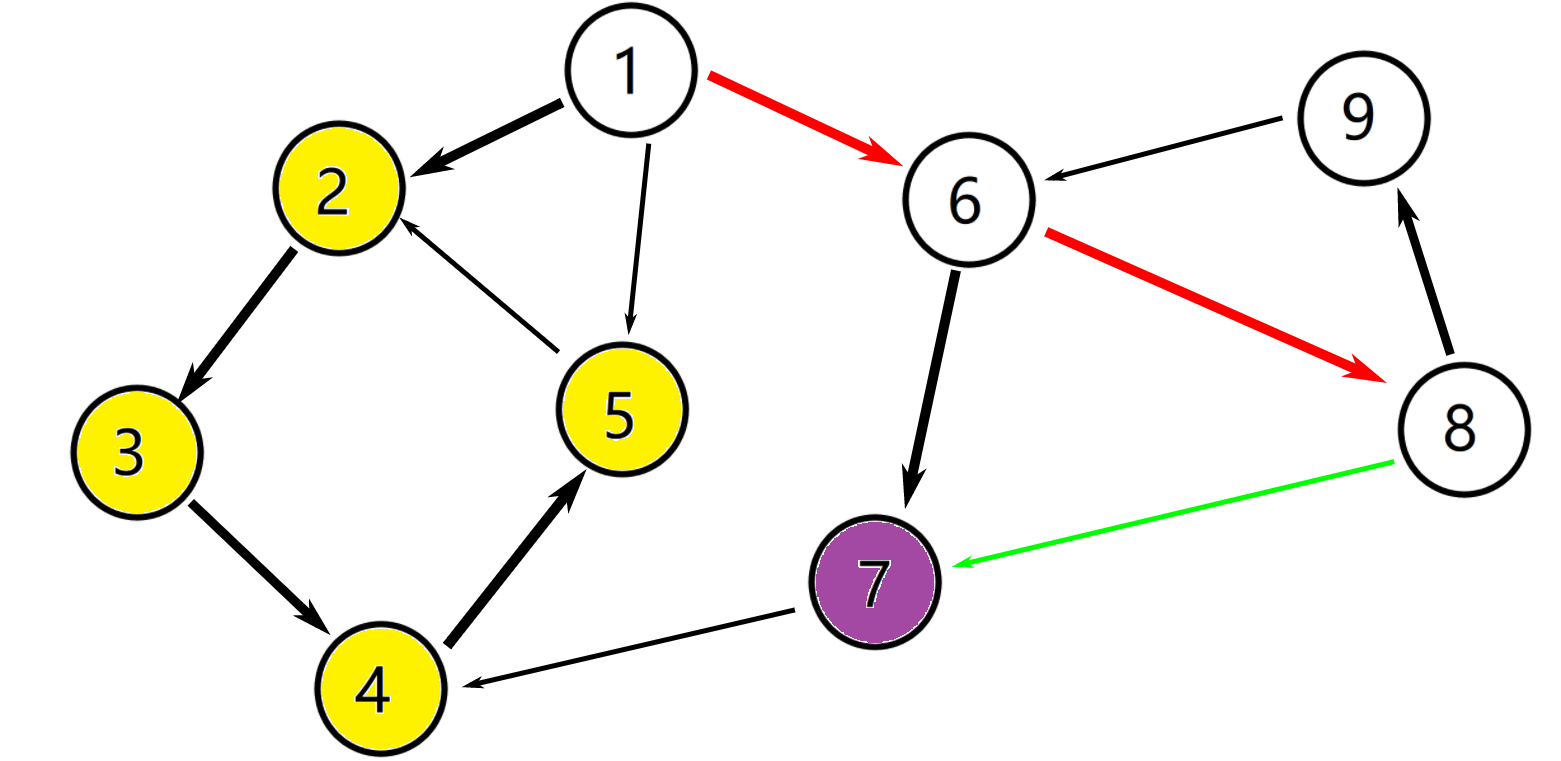
回到 (⑧),它还有一条出边到 (⑨),dfn[9] = low[9] = ++index = 9
入栈 (⑨),此时栈中元素为 (①⑥⑧⑨),vis[9] = true
再往下找到 (⑥),找到了他爷爷(他爸是 (⑧)),dfn[6]被访问过并且还在栈中,说明这个 (⑥) 还在这个强连通分量中。low[9] = min(low[9], dfn[6]) = 6。
接着就是:
low[8] = min(low[8], low[9]) = 6
low[6] = min(low[6], low[8]) = 6
此时 (⑥) 的出边已经找完了,又因为low[6] == dfn[6] == 6,所以 (⑥) 是强连通分量的根,sccnt++,一直弹出栈顶元素,将栈顶元素颜色标记为sccnt,直到栈顶元素为6,最后弹出一次,标记颜色。此时栈中元素为 (①),vis[9] = vis[8] = vis[6] = false。
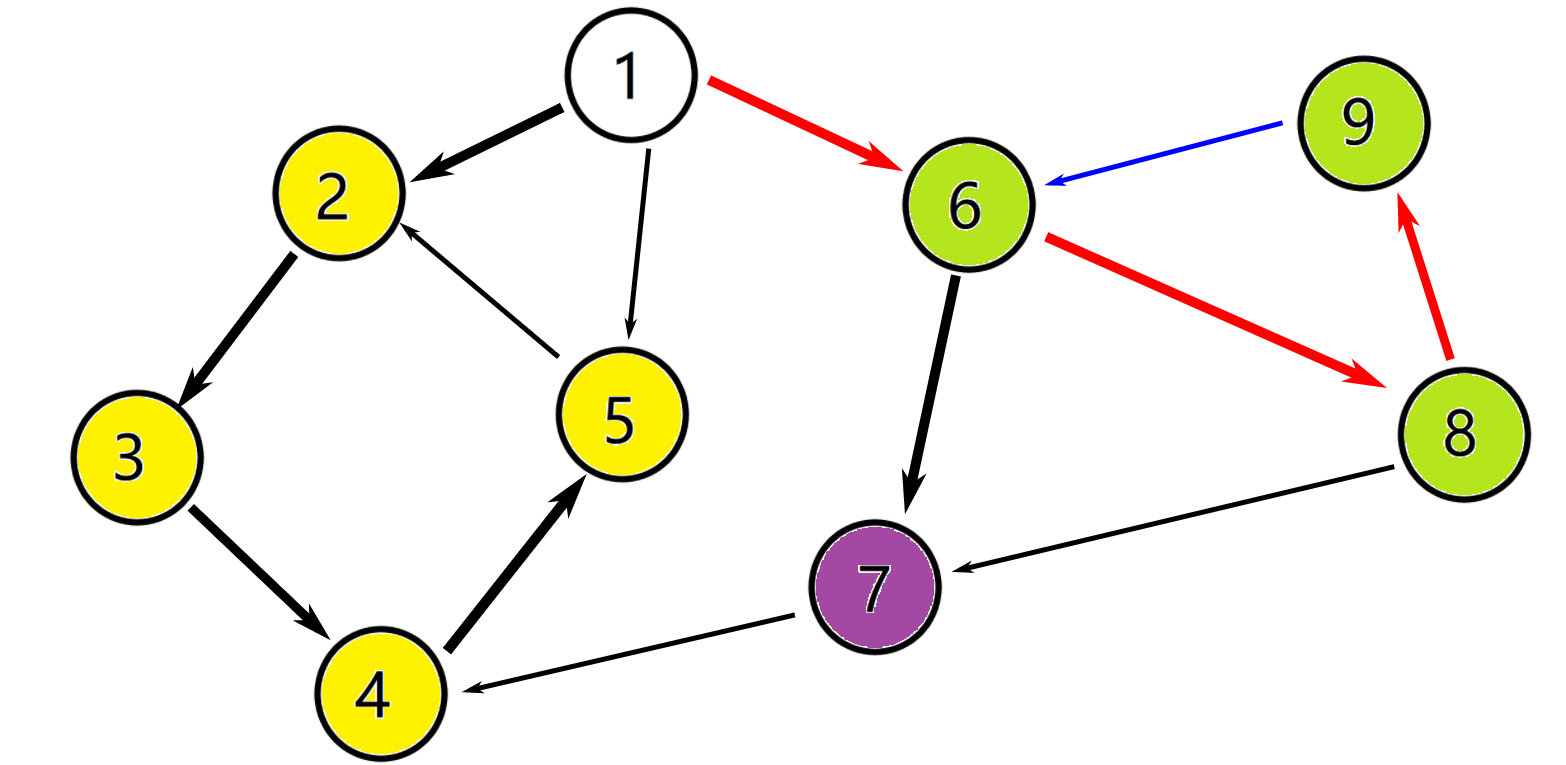
返回到 (①),(①)的出边也已经找完了,因为low[1] == dfn[1] == 1,所以 (①) 是强连通分量的根,sccnt++,弹出栈顶元素(1),将栈顶元素颜色标记为sccnt。此时栈为空,vis[1] = false。
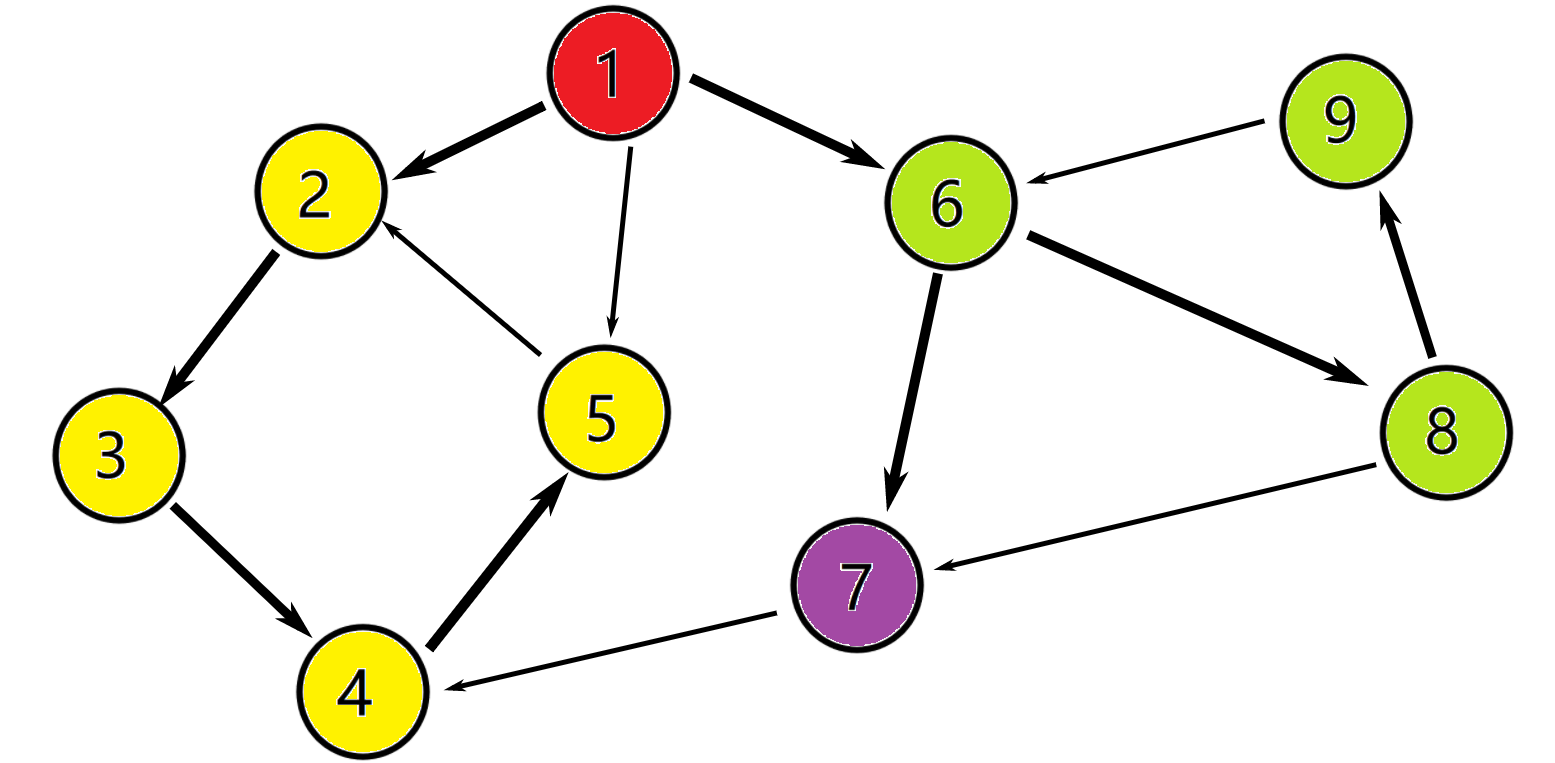
这个时候就完了吗?!
你以为就完了吗?!
然而并没有完,万一只走了一遍tarjan整个图没有找完怎么办呢?!
所以。tarjan的调用要在循环里解决,以使每一个点都被访问到。
代码
下面是tarjan函数的代码:
void tarjan(int v) { //Tarjan算法
dfn[v] = low[v] = ++tot; //标记dfn[]访问顺序,还有low[]的初始值
sta.push(v); //让点v进栈
vis[v] = true; //标记这个点被访问过
for (int i = head[v]; ~i; i = edge[i].next) { //一直循环这个点每一个出度,直到-1表示没有了,这也是为什么memset head数组时要赋-1
int u = edge[i].to; //定义u并把它赋成这条边的终点
if (!dfn[u]) { //如果u没有被访问过
tarjan(u); //找下面这个点
low[v] = min(low[v], low[u]); //这个点low[v]的值就是当前low[]的值与找到的u点的low[]值
} else if (vis[u]) //如果u被访问过了,但是还在队列中
low[v] = min(low[v], dfn[u]); //low[v]就取这个点的low值与循环到的点u的dfn[u]的最小值
}
if (dfn[v] == low[v]) { //如果发现v这个点的dfn[]和low[]相等,说明这个点是一个强连通分量的“根”。
sccnt++; //scc(Strongly Connected Component), cnt(count),就是强连通分量的个数
int u; //定义u变量,作为栈顶元素
do {
u = sta.top(); //将u赋值为sta栈的栈顶元素
vis[u] = false; //将u弹出
sta.pop(); //同上
color[u] = sccnt; //将u标记为这个强连通分量里的点
} while (v != u); //当v == u之后,结束循环
}
}
在主函数里像这样调用tarjan函数:
for (int i = 1; i <= n; i++) //循环每一个点
if (!dfn[i]) tarjan(i); //如果dfn[i]没有值,即这个点被没有访问过,需要访问;
//如果dfn[i]已经有一个值,说明这个点被访问过了,不用担心漏了,
//同时也为了节省时间,就不访问了。
缩点
引入
缩点的定义:把强连通分量看成是一个大点,保留那些不在强连通分量里的边,这样的图就是缩点后的图。
缩点后的图保留了所有不在分量里的边,而且缩点后的图是一个有向无环图(DAG),可以进行拓扑排序。
那么,缩点之后的图,就成了这样:
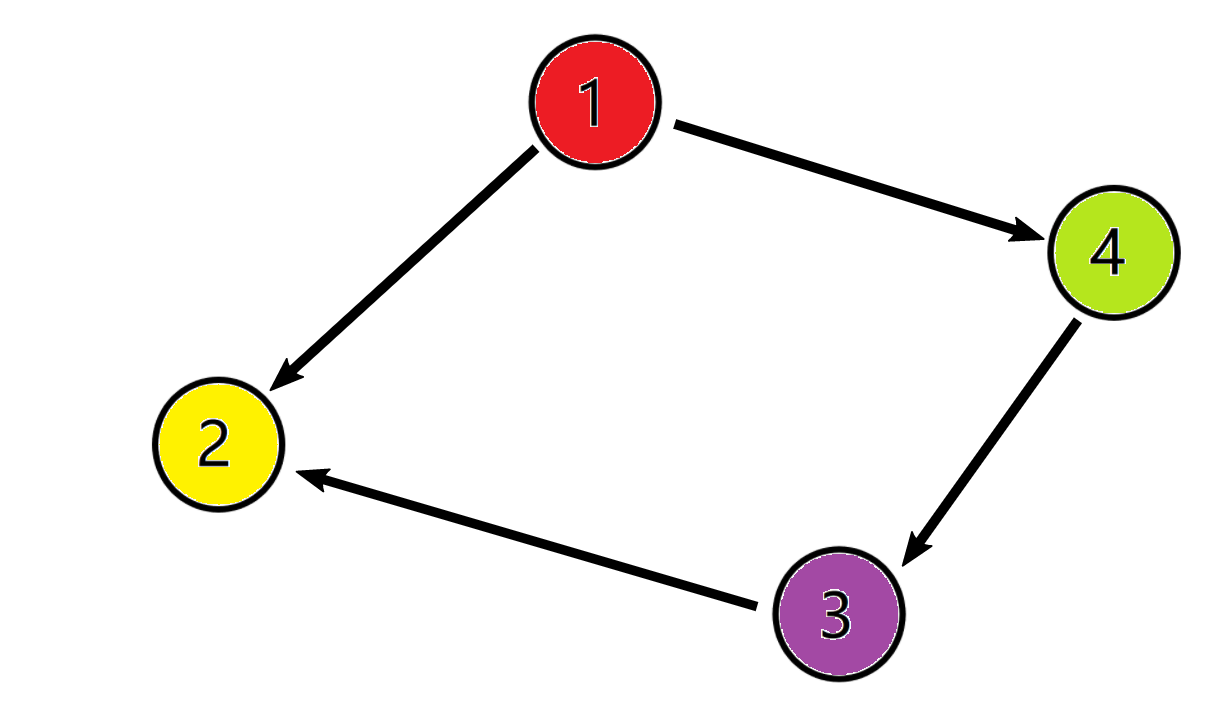
缩点的解决
现在问题来了,怎么储存缩点后的图?
在一开始调用的tarjan函数中,我们已经把同一个强连通分量中的点标记成了相同的颜色。为了重新建立一个缩点后的图,我们先把head[]数组和edge[]数组清空,在读入边的时候,我们把边的起点和终点分别存到from[]数组和to[]数组中。
在建立邻接表储存缩点后的图时,判断这些输入的点是否在同一个 SCC 中,如果不在就连边。
用如下代码建立缩点后的图:
for (int i = 1; i <= m; i++) //循环每一条边
if (color[from[i]] != color[to[i]]) //如果这条边的出发点和终止点不在同一个强连通分量中
add(color[from[i]], color[to[i]]); //就连一条边
【模板】缩点
题目链接:【模板】缩点
审题
这题不仅需要缩点,还要找出一条路径使点权和最大。
因为 强连通分量(SCC) 中点可以互相到达,所以需要缩点使图变成一个有向无环图(DAG),强连通分量 内所有点权和即为缩点后该点的点权。
这题可以使用LPFA算法(Longest Path Fast Algorithm,发明者:沃·兹基硕德)来解决。
把松弛改为扩张:
if (dis[v] > dis[u] + siz[v]) dis[v] = dis[u] + siz[v];
->if (dis[v] < dis[u] + siz[v]) dis[v] = dis[u] + siz[v];
代码
详情请见【题解】P3387 【模板】缩点