0.PTA得分截图

1.本周学习总结
1.1 栈
1.1.1栈的定义及相关概念
-
栈是一种只能在一端进行插入或删除操作的线性表。
-
允许进行插入、删除操作的一端称为栈顶。
-
表的另一端称为栈底。
-
当栈中没有数据元素时,称为空栈。
-
栈的插入操作通常称为进栈或入栈,删除操作通常称为退栈或出栈。
1.1.2栈的存储结构
- 顺序存储,如图所示
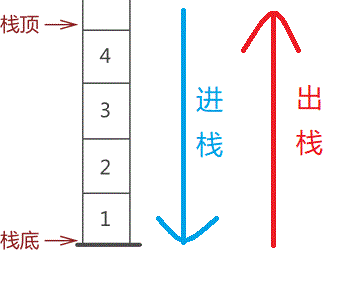
- 链式存储,如图所示

1.1.2栈的结构体定义
代码:
typedef struct
{
int data[MAXSIZE];
int top;
}Stack;
1.1.3栈的初始化
代码:
SeqStack* InitStack()
{
Stack* s;
s = (Stack*)malloc(sizeof(Stack));
s->top = -1;
return s;
}
1.1.4入栈操作
代码:
int PushStack(Stack* s, int x)
{
if(s->top == MAXSIZE - 1)
return 0;
else{
s->top++;
s->data[s->top] = x;
return 1;
}
}
- 图解:
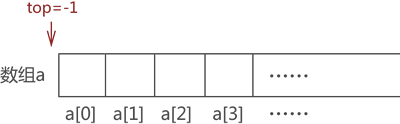
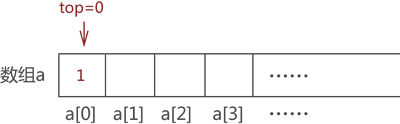
1.1.5出栈操作
代码:
int PopStack(Stack* s, int* x)
{
if(EmptyStack(s))
return 0; //栈空不能出栈
else
{
*x = s->data[s->top];
s->top--;
return 1;
}
}
- 图解:
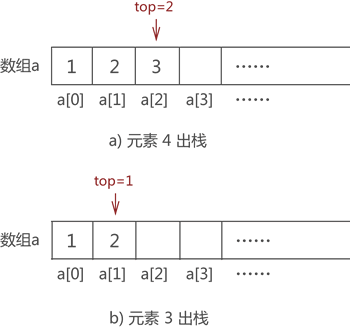

1.1.6判断栈空操作
代码:
int EmptyStack(Stack* s)
{
if(s->top == -1)
return 1;
else
return 0;
}
1.1.7取栈顶元素操作
代码:
DataType GetTop(Stack* s)
{
if(EmptyStack(s))
return 0; //栈空返回
else
return s->data[s->top];
}
1.1.8输出栈操作
代码:
int Print_SeqStack(SeqStack* s)
{
int i;
if(EmptyStack(s))
{
printf("空栈!
");
return 0; //栈空返回
}
printf("当前栈中的元素:
");
for(i = s->top; i >= 0; i--)
printf("%d ", s->data[i]);
printf("
");
return 0;
}
1.1.9链栈
-
定义:将链表的头部作为栈顶,尾部作为栈底
-
链栈的结构体定义
代码:
typedef struct node
{
int data; /*数据域*/
struct node * next; /*指针域*/
}LinkStack;
- 判断空栈
代码:
int StackEmpty(LinkStack *top)
{
if(!top)
return 0;
else
return 1;
}
- 入栈操作,即将数据从链表的头部插入
代码:
LinkStack *Push(LinkStack *top,int x)
{
LinkStack *p;
p=(LinkStack *)malloc(sizeof(LinkStack));
p->data=x; /*设置新结点的值*/
p->next=top; /*将新元素插入栈中*/
top=p; /*将新元素设为栈顶*/
return top;
}
- 出栈操作,即删除链表头部的首元节点
代码:
LinkStack *Pop(LinkStack *top)
{
LinkStack *p;
if(!top)
{
printf("空栈!/n");
return NULL;
}
p=top; //指向被删除的栈顶
top=top->next; //修改栈顶指针
free(p);
return top;
}
- 取栈顶元素
代码:
int GetTop(LinkStack *top)
{
if(!top)
{
printf("空栈!/n");
return 0;
}
return top->data;
}
1.2.1队列的定义及相关概念
-
队列是一种运算受限的线性表,只能选取一个端点进行插入操作,另一个端点进行删除操作。
-
进行插入(进队或入队)的一端称做队尾(rear)。
-
进行删除(出队)的一端称做队首或队头(front)。
1.2.2队列的存储结构
- 顺序存储,如图所示
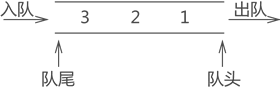
- 链式存储,如图所示

1.2.3队列的结构体定义
代码:
typedef struct
{
int data[MaxSize];
int front,rear;
}Queue;
1.2.4队列的初始化
代码:
void InitQueue(Queue *&queue)
{
q=(Queue *)malloc (sizeof(Queue));
q->front=q->rear=-1;
}
1.2.5入队操作
代码:
int InQueue(Queue *&q,int e)
{
if (q->rear==MaxSize-1) //队满
return 0;
q->rear++;
q->data[q->rear]=e;
return 1;
}
1.2.6出队操作
代码:
int OutQueue(Queue *&q,int &e)
{
if (q->front==q->rear) //队空
return 0;
q->front++;
e=q->data[q->front];
return 1;
}
1.2.7循环队列
-
循环队列判空的条件是front=rear。
-
循环队列判满的条件是front=(rear+1)%MaxSize。
-
循环队列结构体定义
代码:
typedef struct
{
int *base; // 初始化的动态分配存储空间
int front; // 头指针,若队列不空,指向队列头元素
int rear; // 尾指针,若队列不空,指向队列尾元素的下一个位置
}SqQueue;
- 循环队列初始化
代码:
Queue* InitQueue()
{
SqQueue *Q = (SqQueue*)malloc(sizeof(SqQueue));
Q->base = (int *)malloc(MAX_QSIZE * sizeof(int));
Q->front = Q->rear = 0;
return Q;
}
- 循环队列入队
代码:
int InQueue(Queue *Q, int e)
{
if ((Q->rear + 1) % MAX_QSIZE == Q->front) // 满队
return 0;
Q->base[Q->rear] = e;
Q->rear = (Q->rear + 1) % MAXSIZE;
return 1;
}
- 循环队列出队
代码:
int OutQueue0(Queue *Q, int &e)
{
if (Q->front == Q->rear) // 空队
return 0;
e = Q->base[Q->front];
Q->front = (Q->front + 1) % MAXSIZE;
return 1;
}
1.2.8链队
- 链队的结构体定义
代码:
typedef struct QNode
{
int data;
struct QNode * next;
}QNode;
- 链队的初始化
代码:
QNode * initQueue()
{
QNode * queue=(QNode*)malloc(sizeof(QNode));
queue->next=NULL;
return queue;
}
- 链队入队操作
代码:
QNode* enQueue(QNode * rear,int data)
{
QNode * temp=(QNode*)malloc(sizeof(QNode));
temp->data=data;
temp->next=NULL;
rear->next=temp;
rear=temp;
return rear;
}
- 链队出队操作
代码:
void DeQueue(QNode * top,QNode * rear)
{
if (top->next==NULL)
{
printf("队列为空");
return ;
}
QNode * p=top->next;
printf("%d",p->data);
top->next=p->next;
if (rear==p)
rear=top;
free(p);
}
1.3.栈和队列的认识及学习体会
怎么说呢,感觉这次PTA的题目挺难的,要么没思路,要么就是各种调试错误,还是要认真啊。栈跟队列具有很特殊的性质,一个是“先进后出”,一个是只准队首出,队尾入,此外还有链栈、链队、循环队列等,相信运用好这些特性并加以组合定会解决一些难题,获得意想不到的的效果。总之,还是要多多编程,好好编程。
2.PTA实验作业
2.1.题目1:银行业务队列简单模拟
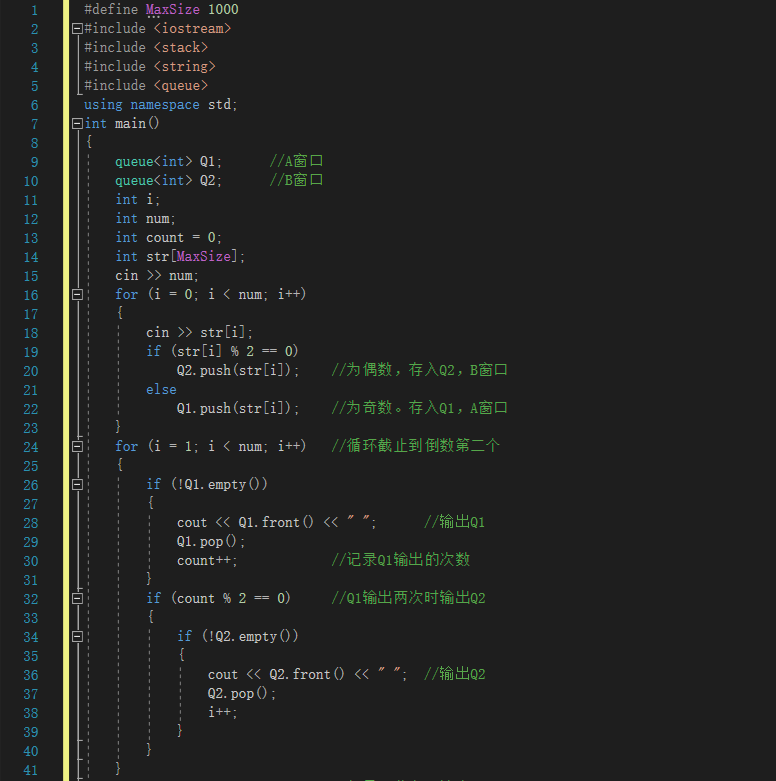
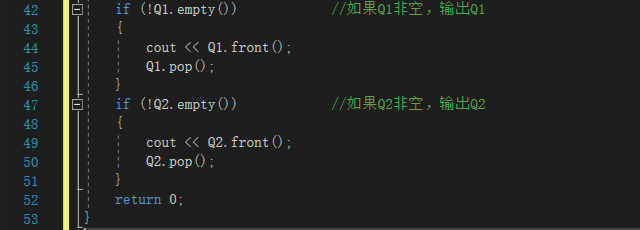
2.1.2本题PTA提交列表说明
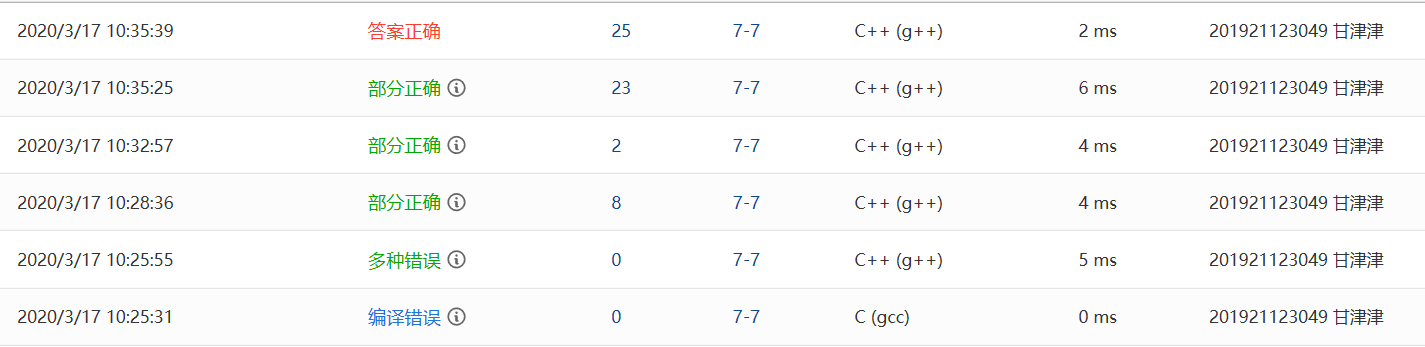
-
编译错误:选错了编译器。
-
多种错误:有段错误、格式错误,以下我展开叙述。
-
段错误:定义str[MaxSize]数组时MaxSize 值取得偏小,改为1000即可。
-
格式错误:没看见题干中“但最后一个编号后不能有多余的空格”一句,后将代码改成:
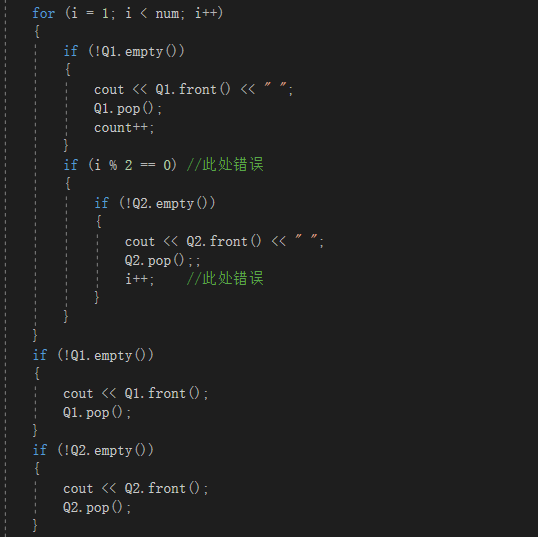
但这并不能解决问题,反而造成部分测试点答案错误。
- 部分正确:部分测试点显示答案错误,由于在输出Q2数据时也应将i加一,因此i就不能作为判断是否轮到Q2输出的变量,因此另设count作为判断变量,测试点就全过了。
2.2 题目2字符串是否对称
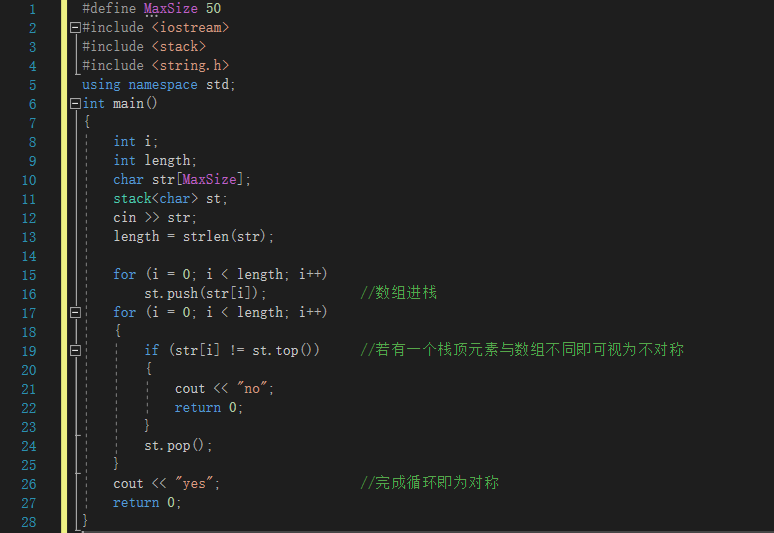
2.1.2本题PTA提交列表说明

- 部分正确:“对称字符串”这一测试点无法通过,经查,为以下错误代码:
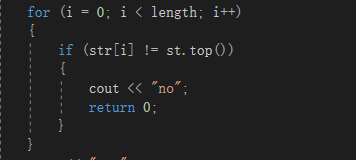
因为没有在for循环内添加出栈语句,导致str[i]一直在与同一个栈顶数据相比较,结果把所有字符串全判为不对称,补充st.pop()一句便通过了测试点。
3.阅读代码
3.1 题目及解题代码
- 题干:
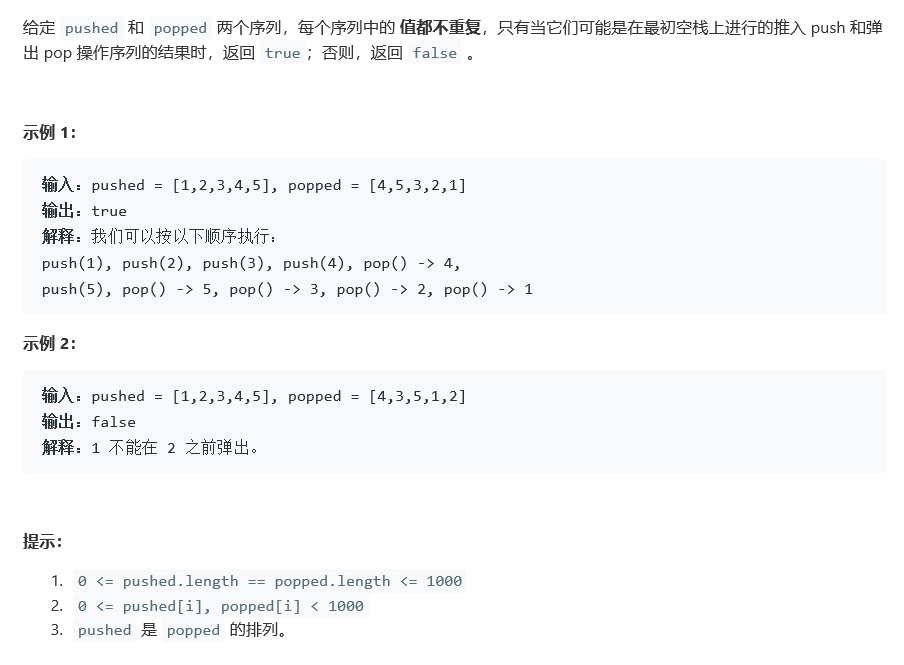
- 代码:

3.1.1 该题的设计思路
-
思路:1.引入一个栈stack。2.把pushed序列按顺序放到栈stack中,每放一个数据对比栈顶与序列popped中元素是否相同,若相同,则栈stack执行pop操作,移到popped的下一个元素,继续对比栈顶与该元素是否相同。
-
正确案例图解:

- 错误案例图解:

-
时间复杂度:以正确的序列为例,假设pushed 和 popped 两个序列的长度为n,则for循环中必定要跑n趟才能将pushed中的所有元素入s栈,而在while循环中也必定需要n趟才能实现s空栈,所以,总次数为2n次,即时间复杂度为O(n)。
-
空间复杂度:O(n)。
3.1.2 该题的伪代码
int n=popped.size(); /*获取序列的大小*/
int i; //用于for循环
stack<int> s; //存放pushed元素
int k=0; //用于统计有几个s栈顶元素与popped首元素相同
for i=0 to i<n
pushed元素依次入s栈
while s非空且k小于n且s栈顶与popped首元素相同
s出栈
k++;
end while
end for
if s非空 then /*如果非空,则返回false*/
return false;
end if
return true;
3.1.3 运行结果

3.1.4分析该题目解题优势及难点
-
解题优势:思路很棒,利用了栈先进后出的特点仅用两层循环就解决了验证栈的序列,总体代码量也较少,时间及空间复杂度较低。
-
本题难点:给出栈的入栈次序判断栈的出栈次序是否合理本身就是个难点,栈的出栈次序存在着多种组合,编程思路就难稿。
3.2 题目及解题代码
- 题目:

- 代码:

3.2.1 该题的设计思路
- 思路:
先排序,然后插入。
假设候选队列为 A,已经站好队的队列为 B.
从 A 里挑身高最高的人 x 出来,插入到 B. 因为 B 中每个人的身高都比 x 要高,因此 x 插入的位置,就是看 x 前面应该有多少人就行了。比如 x 前面有 5 个人,那 x 就插入到队列 B 的第 5 个位置。
- 图解:

-
时间复杂度:两次遍历,一次排序,一次插入,所以时间复杂度为O(n)
-
空间复杂度:O(n)
3.2.2 该题的伪代码
将people按照身高降序排序,相同身高需要按k升序排序
开辟e,将排序后的people存入e
开辟res
for 遍历e
找到位置后插入res
end for
返回res
3.2.3 运行结果

3.2.4分析该题目解题优势及难点
-
优点:思路很棒 ,代码也很简洁,sort、vector语法运用自如。
-
难点:单按h排序并不难,难在还要考虑k的存在。