传送门:http://www.lydsy.com/JudgeOnline/problem.php?id=3677
【题解】
我们发现这样一个结论:如果把某个点作为根,那么蓝线一定是fa-x-son这种情况。
而且一个点作为只能作为一条蓝线的中点。
那么可以dp:
令f[i][0/1]表示x是否为蓝线中点的max值。

具体解释:
1. i不是蓝线中点:那么可能从下面的所有蓝线中点连接上来取个max即可。
2. i是蓝线中点:那么我们去掉一个连接的点,把它改为连线(就是连一条son->i的蓝线),那么i就是蓝线中点了。
那么我们对每个根做一个dp,就是O(n^2)的,可以有50多分?

# include <stdio.h> # include <string.h> # include <algorithm> // # include <bits/stdc++.h> using namespace std; typedef long long ll; typedef long double ld; typedef unsigned long long ull; const int M = 2e5 + 10; const int mod = 1e9+7; # define RG register # define ST static int n; int head[M], nxt[M], to[M], w[M], tot=0; inline void add(int u, int v, int _w) { ++tot; nxt[tot] = head[u]; head[u] = tot; to[tot] = v; w[tot] = _w; } inline void adde(int u, int v, int _w) { add(u, v, _w); add(v, u, _w); } ll f[M][2], ans; inline void dfs(int x, int fa) { f[x][0] = 0, f[x][1] = -1e18; for (int i=head[x]; i; i=nxt[i]) { if(to[i] == fa) continue; dfs(to[i], x); f[x][0] += max(f[to[i]][0], f[to[i]][1] + w[i]); f[x][1] = max(f[x][1], -max(f[to[i]][0], f[to[i]][1] + w[i]) + f[to[i]][0] + w[i]); } f[x][1] += f[x][0]; } int main() { scanf("%d", &n); for (int i=1, u, v, _w; i<n; ++i) { scanf("%d%d%d", &u, &v, &_w); adde(u, v, _w); } for (int i=1; i<=n; ++i) { dfs(i, 0); ans = max(ans, f[i][0]); } printf("%lld ", ans); return 0; }
我们再记录一维,表示根是否在以i为根的子树(不包含i)的子树中。
注意到会出现这种情况:

橙色点为我们dfs下去的根(1号点),真正的根在绿色的这个点,那么红色的点在dp的时候,如果根在绿色这个地方,那么不算蓝色的中点。(可以理解为蓝线中点是按照1号点看下去来维护的)
那么我们加一维之后,其他仍然正常维护。
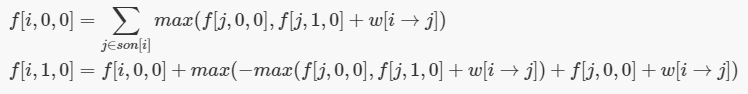
我们令![]()
那么

前两个就是上面的替换一下而已。
后面的我重点解释下。。
f[i,0,1]表示i不是中点,根在i的子树(不包括i)
我们枚举真的根在的子树j,那么假设有这么一条蓝线son[j]->j->i,那么就可以推出max的前半部分:
f[j,1,1](j目前是中点)+w[i->j](蓝线)+(f[i,0,0] - t[j])(去掉这棵子树,其他的蓝线,类比f[i,0,0])
还有一半呢?就是一个特殊情况(上面画图的那个情况)
无论j是不是根,都存在这个情况,所以对f[j,0,0],f[j,0,1]取max。我们同样不能再走这棵子树了,所以要加上(f[i,0,0] - t[j])。接着我们考虑要不要有这根蓝线:我们求出有蓝线的贡献T,如果小于0就不加,大于0就加啊(废话)
那么考虑怎么求贡献:贡献就是
(w[i->j] - t[x] + w[j->k] + f[j,0,0])这个东西。也就是说,我们有(k->i->j)这样一条线。
那么我们对于(- t[x] + w[j->k] + f[j,0,0])维护前缀、后缀max,这样就能求出去掉j的所有k的max了。
f[i,1,1]表示i是中点,根在i的子树(不包括i)
前面那个max和前面一样,然后我们也是要去掉这棵子树,然后连蓝线,i->j,那么i一定是中点。
然后就这么dp。。。

# include <stdio.h> # include <string.h> # include <algorithm> // # include <bits/stdc++.h> using namespace std; typedef long long ll; typedef long double ld; typedef unsigned long long ull; const int M = 4e5 + 10; const int mod = 1e9+7; # define RG register # define ST static int n; int head[M], nxt[M], to[M], w[M], tot=0; inline void add(int u, int v, int _w) { ++tot; nxt[tot] = head[u]; head[u] = tot; to[tot] = v; w[tot] = _w; } inline void adde(int u, int v, int _w) { add(u, v, _w); add(v, u, _w); } ll f[M][2][2], ans; ll t[M], pre[M], suf[M]; int tn; ll sum; inline void dfs(int x, int fa) { for (int i=head[x]; i; i=nxt[i]) { if(to[i] == fa) continue; dfs(to[i], x); } sum = tn = 0; for (int i=head[x]; i; i=nxt[i]) { if(to[i] == fa) continue; t[to[i]] = max(f[to[i]][0][0], f[to[i]][1][0] + w[i]); ++tn; pre[tn] = suf[tn] = f[to[i]][0][0] + w[i] - t[to[i]]; sum = sum + t[to[i]]; } pre[0] = suf[0] = pre[tn+1] = suf[tn+1] = -1e15; for (int i=1; i<=tn; ++i) pre[i] = max(pre[i], pre[i-1]); for (int i=tn; i>=1; --i) suf[i] = max(suf[i], suf[i+1]); f[x][0][0] = sum; if(tn == 0) f[x][1][0] = -1e15; else f[x][1][0] = f[x][0][0] + pre[tn]; f[x][1][1] = -1e15; for (int i=head[x], j=0; i; i=nxt[i]) { if(to[i] == fa) continue; ++j; ll res = max(pre[j-1], suf[j+1]); f[x][0][1] = max(f[x][0][1], // 1: 下面的是中点 max(f[to[i]][1][1] + w[i] + sum - t[to[i]], // 2: 下面的不是中点,这个点也不算是中点(由于不是fa-x-son),但是可以和其他点连接 max(f[to[i]][0][0], f[to[i]][0][1]) + sum - t[to[i]] + max(res + w[i], 0ll))); f[x][1][1] = max(f[x][1][1], max(f[to[i]][0][0], f[to[i]][0][1]) + sum - t[to[i]] + w[i]); } } int main() { scanf("%d", &n); for (int i=1, u, v, _w; i<n; ++i) { scanf("%d%d%d", &u, &v, &_w); adde(u, v, _w); } dfs(1, 0); ans = max(f[1][0][0], f[1][0][1]); printf("%lld ", ans); return 0; }
