官方解题报告:http://blog.sina.com.cn/s/blog_6bddecdc0102v01l.html
A simple brute force problem. http://acm.hdu.edu.cn/showproblem.php?pid=4971
有n个项目,m个问题,解决某个项目会需要解决一些问题,解决项目挣钱,解决问题花钱,某些问题解决之前需解决其他问题。a之前要做b,b之前要做a,也就是会出现环,需要先缩点,参考有向图强连通分量缩点。对于缩点之后的图,参考最大权闭合图的方法建图,源点s到正权点,流量正权值,原图全连inf流量,负权点到汇点t连负权的绝对值。跑出来的最大流也是最小割,用所有正权减去最小割就是可获得的最大权值。

1 #include<cstdio> 2 #include<cstring> 3 #include<vector> 4 #include<stack> 5 #include<queue> 6 #define mt(a,b) memset(a,b,sizeof(a)) 7 using namespace std; 8 const int M=128; 9 const int inf=0x3f3f3f3f; 10 int val[M],cost[M],newcost[M]; 11 vector<int> need[M]; 12 class Tarjan{///有向图强连通分量缩点 13 static const int ME=M*M;///边的个数 14 static const int MV=M;///点的个数 15 int Index,Bcnt,num[MV],belong[MV],dfn[MV],low[MV]; 16 bool instack[MV]; 17 stack<int> s; 18 void tarjan(int u) { 19 dfn[u]=low[u]=++Index; 20 instack[u]=true; 21 s.push(u); 22 int v; 23 for(int i=g.head[u]; ~i; i=g.e[i].next) { 24 v=g.e[i].v; 25 if(!dfn[v]) { 26 tarjan(v); 27 low[u]=min(low[u],low[v]); 28 } else if(instack[v]) { 29 low[u]=min(low[u],dfn[v]); 30 } 31 } 32 if(dfn[u]==low[u]) { 33 Bcnt++; 34 do { 35 v=s.top(); 36 s.pop(); 37 instack[v]=false; 38 belong[v]=Bcnt; 39 num[Bcnt]++; 40 } while(u!=v); 41 } 42 } 43 public: 44 struct G { 45 struct E { 46 int u,v,next; 47 } e[ME]; 48 int le,head[MV]; 49 void init() { 50 le=0; 51 mt(head,-1); 52 } 53 void add(int u,int v) { 54 e[le].u=u; 55 e[le].v=v; 56 e[le].next=head[u]; 57 head[u]=le++; 58 } 59 } g; 60 public: 61 void init() { 62 g.init(); 63 Index=Bcnt=0; 64 mt(num,0); 65 mt(dfn,0); 66 mt(low,0); 67 mt(instack,0); 68 while(!s.empty()) s.pop(); 69 } 70 void add(int u,int v) { 71 g.add(u,v); 72 } 73 void solve(int n) {///传入点数,点下标1开始 74 for(int i=1; i<=n; i++) { 75 if(!dfn[i]) { 76 tarjan(i); 77 } 78 } 79 } 80 int getbcnt() {///强连通分量的个数 81 return Bcnt; 82 } 83 int getbelong(int id) {///属于哪个分量,分量下标1开始 84 return belong[id]; 85 } 86 int getnum(int id) {///某个分量的点的个数 87 return num[id]; 88 } 89 }tarjan; 90 class Dinic { ///最大流 O(MV^2*ME) 91 typedef int typef;///流量的类型 92 static const int ME=M*M;///边的个数 93 static const int MV=M;///点的个数 94 int temp[MV],cur[MV],level[MV],path[MV]; 95 bool used[MV]; 96 queue<int> q; 97 typef flow; 98 bool bfs(int s,int t) { 99 mt(level,-1); 100 while(!q.empty()) q.pop(); 101 q.push(s); 102 level[s]=1; 103 while(!q.empty()) { 104 int u=q.front(); 105 q.pop(); 106 for(int i=g.head[u]; ~i; i=g.e[i].next) { 107 int v=g.e[i].v; 108 if(level[v]==-1&&g.e[i].flow) { 109 level[v]=level[u]+1; 110 q.push(v); 111 if(v==t) return true; 112 } 113 } 114 } 115 return false; 116 } 117 struct G { 118 struct E { 119 int u,v,next; 120 typef flow; 121 } e[ME]; 122 int le,head[MV]; 123 void init() { 124 le=0; 125 mt(head,-1); 126 } 127 void add(int u,int v,typef flow) { 128 e[le].u=u; 129 e[le].v=v; 130 e[le].flow=flow; 131 e[le].next=head[u]; 132 head[u]=le++; 133 } 134 } g; 135 public: 136 typef getflow() { 137 return flow; 138 } 139 void init() { 140 g.init(); 141 } 142 void add(int u,int v,typef flow) { 143 g.add(u,v,flow); 144 g.add(v,u,0); 145 } 146 void solve(int s,int t) { 147 int p,tempp; 148 typef now; 149 bool flag; 150 flow=0; 151 while(bfs(s,t)) { 152 for(int i=0; i<MV; i++) { 153 temp[i]=g.head[i]; 154 used[i]=true; 155 } 156 p=1; 157 path[p]=s; 158 while(p) { 159 int u=path[p]; 160 if(u==t) { 161 now=inf; 162 for(int i=1; i<p; i++) { 163 now=min(now,g.e[cur[path[i]]].flow); 164 } 165 flow+=now; 166 for(int i=1; i<p; i++) { 167 int j=cur[path[i]]; 168 g.e[j].flow-=now; 169 g.e[j^1].flow+=now; 170 if(!g.e[j].flow) tempp=i; 171 } 172 p=tempp; 173 } else { 174 flag=false; 175 for(int i=temp[u]; ~i; i=g.e[i].next) { 176 int v=g.e[i].v; 177 if(used[v]&&g.e[i].flow&&level[u]+1==level[v]) { 178 cur[u]=i; 179 temp[u]=g.e[i].next; 180 flag=true; 181 path[++p]=v; 182 break; 183 } 184 } 185 if(flag) continue; 186 p--; 187 used[u]=false; 188 } 189 } 190 } 191 } 192 } dinic; 193 int main(){ 194 int t,n,m; 195 while(~scanf("%d",&t)){ 196 for(int cas=1;cas<=t;cas++){ 197 scanf("%d%d",&n,&m); 198 for(int i=1;i<=n;i++){ 199 scanf("%d",&val[i]); 200 } 201 for(int i=1;i<=m;i++){ 202 scanf("%d",&cost[i]); 203 } 204 for(int i=1,num,id;i<=n;i++){ 205 scanf("%d",&num); 206 need[i].clear(); 207 while(num--){ 208 scanf("%d",&id); 209 need[i].push_back(id+1); 210 } 211 } 212 tarjan.init(); 213 for(int i=1;i<=m;i++){ 214 for(int j=1,op;j<=m;j++){ 215 scanf("%d",&op); 216 if(op){ 217 tarjan.add(i,j); 218 } 219 } 220 } 221 tarjan.solve(m); 222 dinic.init(); 223 for(int i=0;i<tarjan.g.le;i++){ 224 int u=tarjan.g.e[i].u; 225 int v=tarjan.g.e[i].v; 226 u=tarjan.getbelong(u); 227 v=tarjan.getbelong(v); 228 if(u!=v){ 229 dinic.add(u+n,v+n,inf); 230 } 231 } 232 for(int i=1;i<=n;i++){ 233 int len=need[i].size(); 234 for(int j=0;j<len;j++){ 235 dinic.add(i,n+tarjan.getbelong(need[i][j]),inf); 236 } 237 } 238 int s=0,t=n+m+1; 239 int sum=0; 240 for(int i=1;i<=n;i++){ 241 dinic.add(s,i,val[i]); 242 sum+=val[i]; 243 } 244 mt(newcost,0); 245 for(int i=1;i<=m;i++){ 246 newcost[tarjan.getbelong(i)]+=cost[i]; 247 } 248 for(int i=1;i<=tarjan.getbcnt();i++){ 249 dinic.add(i+n,t,newcost[i]); 250 } 251 dinic.solve(s,t); 252 printf("Case #%d: %d ",cas,sum-dinic.getflow()); 253 } 254 } 255 return 0; 256 }
A simple water problem http://acm.hdu.edu.cn/showproblem.php?pid=4974
每次最多贡献2分,结果至少是最大值,偶数就sum/2,奇数还要加一。

1 #include<cstdio> 2 #include<algorithm> 3 using namespace std; 4 typedef __int64 LL; 5 int main(){ 6 int t,n,a; 7 while(~scanf("%d",&t)){ 8 for(int cas=1;cas<=t;cas++){ 9 scanf("%d",&n); 10 int big=0; 11 LL sum=0; 12 while(n--){ 13 scanf("%d",&a); 14 big=max(big,a); 15 sum+=a; 16 } 17 LL ans=sum/2; 18 if(sum&1) ans++; 19 printf("Case #%d: %I64d ",cas,max((LL)big,ans)); 20 } 21 } 22 return 0; 23 }
A simple probability problem. http://acm.hdu.edu.cn/showproblem.php?pid=4978
这种做法比较好理解。
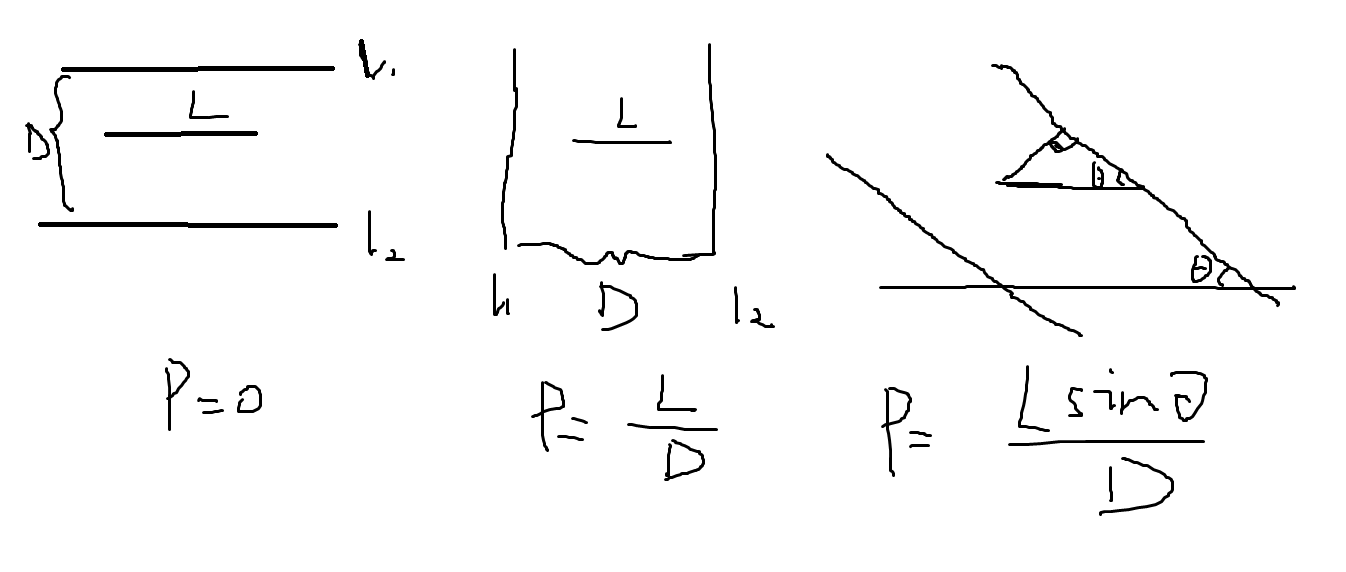
题目说是有间距为D的等间距的无穷条平行线,考虑一个线段长度为L的概率。题目说点在直径为D的圆内,所以L<=D.
平行时除了一次重合,别的都没有相交,概率约等于0.垂直的概率就是L/D。考虑通用情况,设平行线与我们的线段L夹角为θ。
则要转化成垂直然后计算概率,那么就是长度Lsinθ在D之间的概率。综上所述,对任意夹角θ,有通用公式概率P=L*sin(θ)/D.经检验,0度90度满足公式。
因为是随机放球,相当于夹角θ是随机的,L,D都是定值,那么概率就等于sin(θ)在0到180的均值。因为是随机,所以每个角度等概率,所以是均值。
为了计算sin(θ)的均值,打不出来了。考虑用面积,就是定积分来求。因为面积=定积分=底乘高,如果把函数图像拉直成一个矩形,面积就是y*(x2-x1)。
y就是均值,x1=0,x2=π。那个是派,3.1415926,是弧度中的180度.
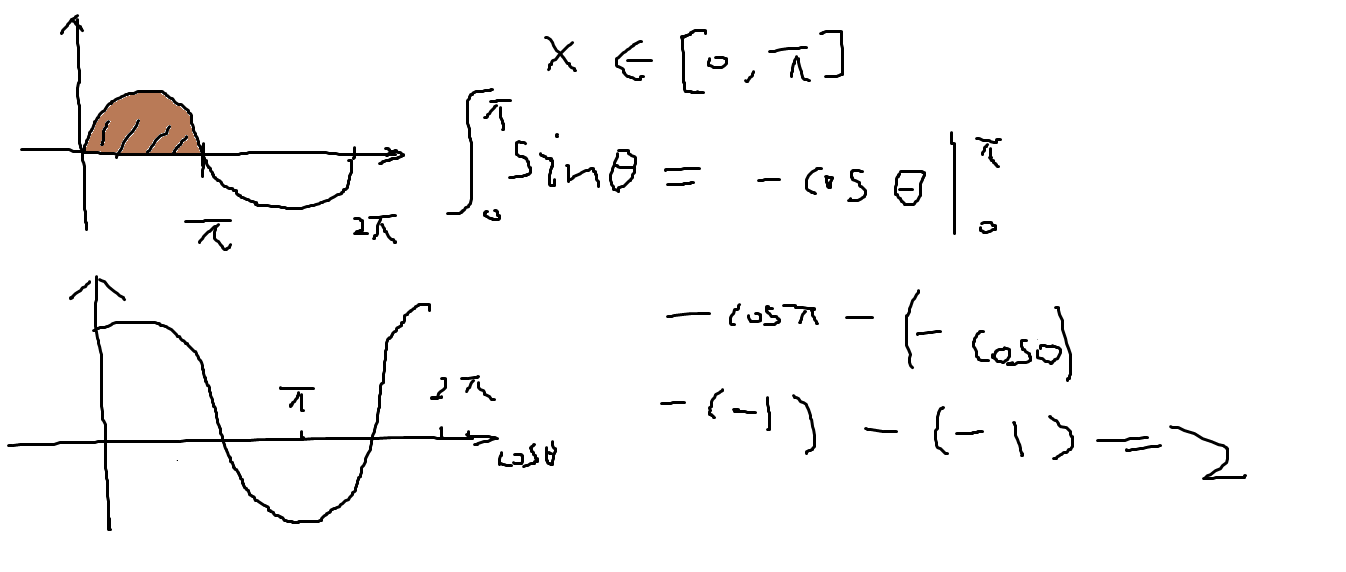
求出来发现面积是2,也就是y*(pi-0)=2,那么sin(θ)的均值也就是y就等于2/pi. pi是派 3.14。
L*sin(θ)/D 等于下方结果。
所以官方题解的第一句话证毕。

现在我们的问题是圆内有n个点,他们之间两两间有线段,求和直线相交的概率。
通俗的想,里面的肯定没有外面的好,如果外面的相交的长度肯定大于里面的,这里就可以想到凸包。
然后就套凸包模板。然后点就只剩下凸包上的了。
然后就变成了求凸包和直线相交的概率=P。
接着,凸包要和直线相交,那么必然有凸包上的两条边和直线相交了。因为直线穿过了这个凸包,如果只和一条边相交,那就重合,是边界条件,对概率影响几乎为零,不考虑。
紧接着,凸包和直线相交,不可能穿过3条边,或者更多,因为是凸包。所以我们得到一个朴素的结论,凸包和直线相交的情况,就是有且仅有2条边与直线相交。
定义P i 表示 第i 条边和直线相交的概率。
则我们所求的凸包和直线相交的概率就是 P=1/2* sum(Pi) (i=1,2,...n) 其中pi 是线段 i 与直线相交的概率。我们把所有凸包的边枚举了,把他们的概率加起来。
之所以要除以2,因为一条直线一定会穿过两条边,那么对每一条直线,我们在概率里都算了两次,所以求和后除以2.
P=1/2* sum(Pi) (i=1,2,...n)
记@=3.1415926
我们刚才推出了一条边的概率 Pi =2*Li/(@*D) . 带入上式
P=(1/2) * sum ( 2*Li / ( @ *D ) ) (i=1,2,...n)
除了Li 其他都可以提出来
P = (1/ ( @ * D ) ) * sum( Li ) (i=1,2,...n)
@是派,实在难打,好了 sum Li 不就是周长吗。

1 #include<cstdio> 2 #include<cmath> 3 #include<algorithm> 4 using namespace std; 5 const double pi=acos(-1.0); 6 const double eps=1e-8; 7 const int M=128; 8 struct point{ 9 double x,y; 10 }p[M],res[M]; 11 bool operator < (const point &l, const point &r) { 12 return l.y < r.y || (fabs(l.y- r.y)<eps && l.x < r.x); 13 } 14 class ConvexHull { //凸包 15 bool mult(point sp, point ep, point op) {//>包括凸包边上的点,>=不包括 16 return (sp.x - op.x) * (ep.y - op.y)>= (ep.x - op.x) * (sp.y - op.y); 17 } 18 public: 19 int graham(int n,point p[],point res[]) {//多边形点个数和点数组,凸包存res 20 sort(p, p + n); 21 if (n == 0) return 0; 22 res[0] = p[0]; 23 if (n == 1) return 1; 24 res[1] = p[1]; 25 if (n == 2) return 2; 26 res[2] = p[2]; 27 int top=1; 28 for (int i = 2; i < n; i++) { 29 while (top && mult(p[i], res[top], res[top-1])) top--; 30 res[++top] = p[i]; 31 } 32 int len = top; 33 res[++top] = p[n - 2]; 34 for (int i = n - 3; i >= 0; i--) { 35 while (top!=len && mult(p[i], res[top],res[top-1])) top--; 36 res[++top] = p[i]; 37 } 38 return top; // 返回凸包中点的个数 39 } 40 } gx; 41 double Distance(point p1,point p2) { 42 return sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y)); 43 } 44 int main(){ 45 int t,n,d; 46 while(~scanf("%d",&t)){ 47 for(int cas=1;cas<=t;cas++){ 48 scanf("%d%d",&n,&d); 49 for(int i=0;i<n;i++){ 50 scanf("%lf%lf",&p[i].x,&p[i].y); 51 } 52 int lr=gx.graham(n,p,res); 53 res[lr]=res[0]; 54 double sum=0; 55 for(int i=0;i<lr;i++){ 56 sum+=Distance(res[i],res[i+1]); 57 } 58 printf("Case #%d: %.4f ",cas,sum/pi/d); 59 } 60 } 61 return 0; 62 }
其实我是想说,这种做法比较好理解,虽然不是正解,但只要精度够了,也能过。
上面说过,一条线,长度L,那么概率是 通用公式P=L*sin(θ)/D. 角度是0到180,等可能,而对于凸包,某一个角度和直线相交的概率就是这个角度下凸包最远距离。
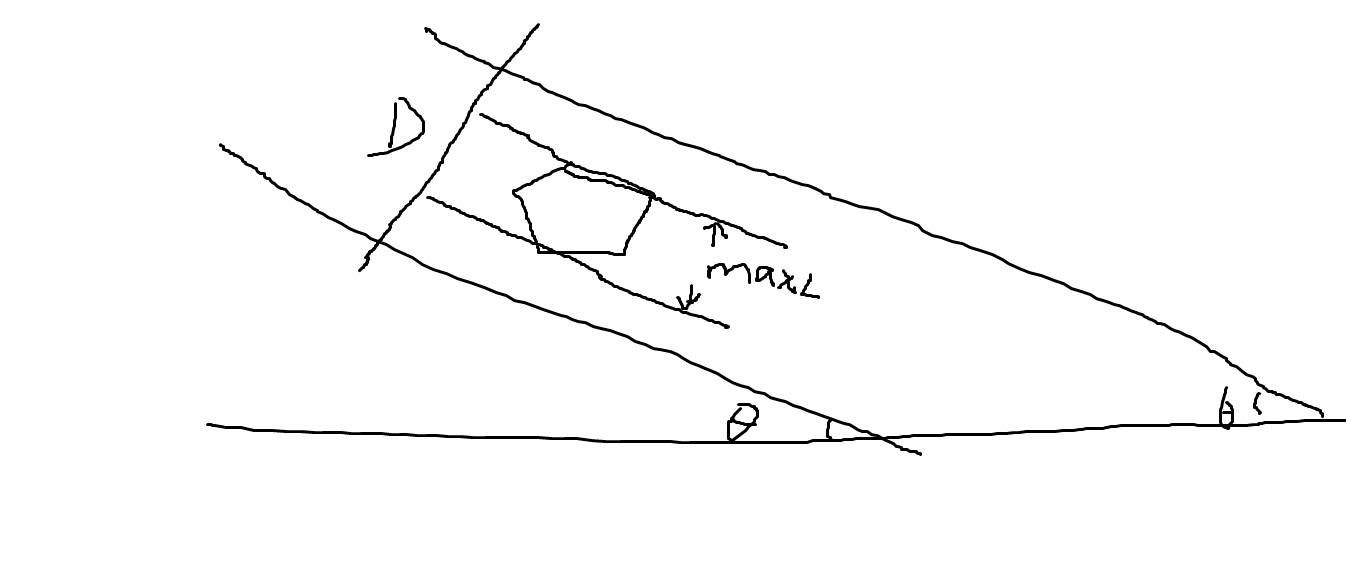
如图,在某一个角度θ下,与直线相交的概率就是凸包在与直线垂直的方向上的投影。maxL。 为了求这个投影,可以on的枚举凸包的点,计算到直线的最近距离的点。
然后因为这些点在直线上是递增的。所以取最大的和最小的,就是最远的两个点。然后就可以算出maxl, maxl/D就是当前角度下的概率,我们自定义个增量枚举角度。
对每一个角度都求一个maxl, 最后 sum(maxLi)/num 就是平均长度, 再/D就是概率。

1 #include<cstdio> 2 #include<cmath> 3 #include<algorithm> 4 using namespace std; 5 const double pi=acos(-1.0); 6 const double eps=1e-8; 7 const int M=128; 8 struct point { 9 double x,y; 10 } p[M],res[M]; 11 bool operator < (const point &l, const point &r) { 12 return l.y < r.y || (fabs(l.y- r.y)<eps && l.x < r.x); 13 } 14 class ConvexHull { //凸包 15 bool mult(point sp, point ep, point op) {//>包括凸包边上的点,>=不包括 16 return (sp.x - op.x) * (ep.y - op.y)>= (ep.x - op.x) * (sp.y - op.y); 17 } 18 public: 19 int graham(int n,point p[],point res[]) {//多边形点个数和点数组,凸包存res 20 sort(p, p + n); 21 if (n == 0) return 0; 22 res[0] = p[0]; 23 if (n == 1) return 1; 24 res[1] = p[1]; 25 if (n == 2) return 2; 26 res[2] = p[2]; 27 int top=1; 28 for (int i = 2; i < n; i++) { 29 while (top && mult(p[i], res[top], res[top-1])) top--; 30 res[++top] = p[i]; 31 } 32 int len = top; 33 res[++top] = p[n - 2]; 34 for (int i = n - 3; i >= 0; i--) { 35 while (top!=len && mult(p[i], res[top],res[top-1])) top--; 36 res[++top] = p[i]; 37 } 38 return top; // 返回凸包中点的个数 39 } 40 } tubao; 41 double xmult(point p1,point p2,point p0) { 42 return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y); 43 } 44 double Distance(point p1,point p2) { 45 return sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y)); 46 } 47 struct line { 48 point a,b; 49 }; 50 point intersection(point u1,point u2,point v1,point v2) { 51 point ret=u1; 52 double t=((u1.x-v1.x)*(v1.y-v2.y)-(u1.y-v1.y)*(v1.x-v2.x)) /((u1.x-u2.x)*(v1.y-v2.y)-(u1.y-u2.y)*(v1.x-v2.x)); 53 ret.x+=(u2.x-u1.x)*t; 54 ret.y+=(u2.y-u1.y)*t; 55 return ret; 56 } 57 point ptoline(point p,line l) {//点到直线上的最近点 58 point t=p; 59 t.x+=l.a.y-l.b.y,t.y+=l.b.x-l.a.x; 60 return intersection(p,t,l.a,l.b); 61 } 62 int main() { 63 int t,n; 64 double D; 65 while(~scanf("%d",&t)) { 66 int cas=1; 67 while(t--) { 68 scanf("%d%lf",&n,&D); 69 for(int i=0; i<n; i++) { 70 scanf("%lf%lf",&p[i].x,&p[i].y); 71 } 72 int lr=tubao.graham(n,p,res); 73 double sum=0; 74 int num=0; 75 double add=180.0/5000; 76 for(double jiao=0; jiao<180; jiao+=add) { 77 double xita=jiao/180*pi; 78 line ll; 79 ll.a.x=ll.a.y=0; 80 ll.b.x=1; 81 ll.b.y=tan(xita); 82 point p1=ptoline(res[0],ll); 83 point p2=p1; 84 for(int i=1; i<lr; i++) { 85 point p3=ptoline(res[i],ll); 86 p1=max(p1,p3); 87 p2=min(p2,p3); 88 } 89 sum+=Distance(p1,p2); 90 num++; 91 } 92 printf("Case #%d: %.4f ",cas++,sum/D/num); 93 } 94 } 95 return 0; 96 }
end
