算法

查找

二分查找

时间复杂度： O(logn)
空间复杂度: O(1) 它对存储空间的要求是常数数量，不随着元素多少而变化。所以它的空间复杂度为O(1)。
当我们要从一个序列中查找一个元素的时候，二分查找是一种非常快速的查找算法，二分查找又叫折半查找。
它对要查找的序列有两个要求，
一是该序列必须是有序的（即该序列中的所有元素都是按照大小关系排好序的，升序和降序都可以，本文假设是升序排列的），
二是该序列必须是顺序存储的。图1展示的就是一个能进行二分查找的序列。

二分查找算法的原理如下：
1. 如果待查序列为空，那么就返回-1，并退出算法；这表示查找不到目标元素。
2. 如果待查序列不为空，则将它的中间元素与要查找的目标元素进行匹配，看它们是否相等。
3. 如果相等，则返回该中间元素的索引，并退出算法；此时就查找成功了。
4. 如果不相等，就再比较这两个元素的大小。
5. 如果该中间元素大于目标元素，那么就将当前序列的前半部分作为新的待查序列；这是因为后半部分的所有元素都大于目标元素，它们全都被排除了。
6. 如果该中间元素小于目标元素，那么就将当前序列的后半部分作为新的待查序列；这是因为前半部分的所有元素都小于目标元素，它们全都被排除了。
7. 在新的待查序列上重新开始第1步的工作。

def binary_search(l, item):
    low = 0
    high = len(l)-1
    count = 0
    while low <= high:
        count += 1
        mid = (low+high)//2
        guess = l[mid]
        if guess == item:
            return mid
        if guess < item:
            low = mid + 1
        else:
            high = mid - 1
    else:
        return None


l = [i for i in range(129)]

index = binary_search(l, 0)
print(index)

递归

1、明确递归终止条件；

2、给出递归终止时的处理办法；

3、提取重复的逻辑，缩小问题规模。

排序

冒泡排序

冒泡排序（英语：Bubble Sort）是一种简单的排序算法。

　　它重复地遍历要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。遍历数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

算法原理：

• 比较相邻的元素。如果第一个比第二个大（升序），就交换他们两个。
• 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
• 针对所有的元素重复以上的步骤，除了最后一个。
• 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较

# 方式一
def bubble_sort(arr):
    n = len(arr)
    for j in range(n - 1):
        for i in range(n - 1 - j):
            if arr[i] > arr[i + 1]:
                arr[i], arr[i + 1] = arr[i + 1], arr[i]

# 方式二： 优化方式一
def bubble_sort3(arr):
    for j in range(len(arr)-1, 0, -1):
        exchange = False 
        for i in range(0, j):
            if arr[i] > arr[i + 1]:
                arr[i], arr[i + 1] = arr[i + 1], arr[i]
                exchange = True
        if not exchange:
            break

插入排序

• 从第二个元素开始和前面的元素进行比较，如果前面的元素比当前元素大，则将前面元素 后移，当前元素依次往前，直到找到比它小或等于它的元素插入在其后面

• 然后选择第三个元素，重复上述操作，进行插入

• 依次选择到最后一个元素，插入后即完成所有排序

def insertion_sort(arr):
    """插入排序"""
    # 第一层for表示循环插入的遍数
    for i in range(1, len(arr)):
        # 设置当前需要插入的元素
        current = arr[i]
        # 与当前元素比较的比较元素
        pre_index = i - 1
        while pre_index >= 0 and arr[pre_index] > current:
            # 当比较元素大于当前元素则把比较元素后移
            arr[pre_index + 1] = arr[pre_index]
            # 往前选择下一个比较元素
            pre_index -= 1
        # 当比较元素小于当前元素，则将当前元素插入在 其后面
        arr[pre_index + 1] = current
    return arr

选择排序

算法思想：第一趟从n个元素的数据序列中选出关键字最小/大的元素并放在最前/后位置，下一趟从n-1个元素中选出最小/大的元素并放在最前/后位置。以此类推，经过n-1趟完成排序。

时间复杂度： O(n^2)

import random

def findSmallest(_list):
    smallest = _list[0]
    smallest_index = 0
    for i in range(1, len(_list)):
        if smallest > _list[i]:
            smallest = _list[i]
            smallest_index = i
    return smallest_index


def selectionSort(_list):
    new_list = []
    for i in range(len(_list)):
        smallest_index = findSmallest(_list)
        new_list.append(_list.pop(smallest_index))
    return new_list


def select_sort2(li):

    for i in range(len(li)-1): #循环趟数
        min_position=i #将无序区的最小位置进行保存
        for j in range(i+1,len(li)): #再从剩余未排序元素中继续寻找最小元素，然后放到已排序序列的末尾
            if li[j]<li[min_position]:
　　　　　　      min_position=j
　　　　 li[min_position],li[i]=li[i],li[min_position]

L = list(range(10))
random.shuffle(L)
print(L)
new_list = selectionSort(L)
print(new_list)                

快速排序

时间复杂度：O(n*logn)， 平均情况下， 涉及O（logn） 层，每层O(n) 个元素

在序列中找一个划分值，通过一趟排序将未排序的序列排序成 独立的两个部分，其中左边部分序列都比划分值小，右边部分的序列比划分值大，此时划分值的位置已确认，然后再对这两个序列按照同样的方法进行排序，从而达到整个序列都有序的目的。

 

# python语法
def quicksork(array):
    if len(array) < 2:
        return array
    else:
        tmp = array[0]
        less = [i for i in array if i < tmp]
        greater = [i for i in array if i > tmp]
        return quicksork(less)+ [tmp] + quicksork(greater)

# C风格
def quicksort2(array, left, right):
    s_left = left
    s_right = right
    if left < right:
        tmp = array[left]
        while left < right:
            while right > left and tmp < array[right]:
                right -= 1
            else:
                array[left] = array[right]
            while left<right and  array[left] < tmp:
                left += 1
            else:
                array[right] = array[left]
        array[left] = tmp
        quicksort2(array, s_left, left-1 )
        quicksort2(array, left+1, s_right)

# C风格
def quick_sort(L):
    return q_sort(L, 0, len(L) - 1)

def q_sort(L, left, right):
    if left < right:
        pivot = Partition(L, left, right)

        q_sort(L, left, pivot - 1)
        q_sort(L, pivot + 1, right)
    return L

def Partition(L, left, right):
    pivotkey = L[left]
    while left < right:
        while left < right and L[right] >= pivotkey:
            right -= 1
        L[left] = L[right]
        while left < right and L[left] <= pivotkey:
            left += 1
        L[right] = L[left]

    L[left] = pivotkey
    return left

堆排序

1、什么是堆？

采用树形结构‘实现优先队列的一种有效技术称为堆。堆就是节点里存储数据的完全二叉树。堆包括大根堆和小根堆：

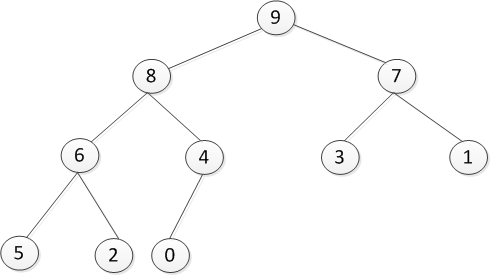
• 大顶堆　一颗完全二叉树，满足任一节点都比其孩子节点大，在堆排序算法中用于升序排列。

• 小顶堆　 一颗完全二叉树，满足任一节点都比其孩子节点小，在堆排序算法中用于降序排列。

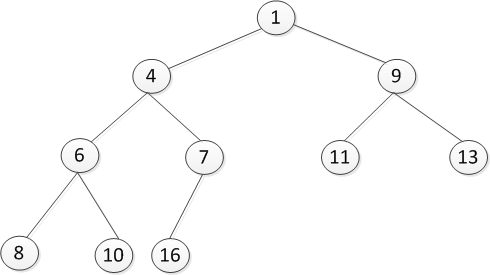
2、堆向下调整性质

　　可以看到，如果出现上图这种情况，根节点是4不符合大顶堆，但是其他节点符合，可以通过向下调整，将12放到4的位置，然后4放到12的位置，但是明显是不可行的，于是在6和9中选取9放到以前12的位置，于是出现下面的结果：

二、堆排序

1、算法步骤

• 建立堆
• 得到堆顶元素为最大元素
• 去掉堆顶，将堆最后一个元素放到堆顶，此时可通过一次调整重新使堆有序
• 堆顶元素为第二大元素
• 重复步骤三，直到堆为空

2、实现

def sift(li, start, last):
    temp = li[start] #表示每一棵树顶部的元素
    i = start
    j = 2 * i + 1 #表示i节点左侧孩子的下标位置
    while j <= last:  # 退出循环条件：当前位置是叶子节点，j的位置超过了last
        if j + 1 <= last and li[j + 1] > li[j]:
            j = j + 1  # 如果右边的孩子更大，j就选择右边孩子
        if temp < li[j]:
            li[i] = li[j]
            i = j
            j = 2 * i + 1
        else:  # 退出循环条件：temp的值大于两个孩子的值
            li[i] = temp
            break
    else:
        li[i] = temp


def heapSort(li):
    # 建立堆
    n = len(li)
    for i in range(n // 2 - 1, -1, -1):#从最后一个非叶子节点的下标位置开始循环
        sift(li, i, n - 1)
    # 出数
    for i in range(n - 1, -1, -1):
        li[i], li[0] = li[0], li[i]
        sift(li, 0, i - 1)


li = [12, 58, 69, 2, 0, 5, 4, 3, 56]
heapSort(li)
print(li)#[0, 2, 3, 4, 5, 12, 56, 58, 69]

这是怎么实现的呢？

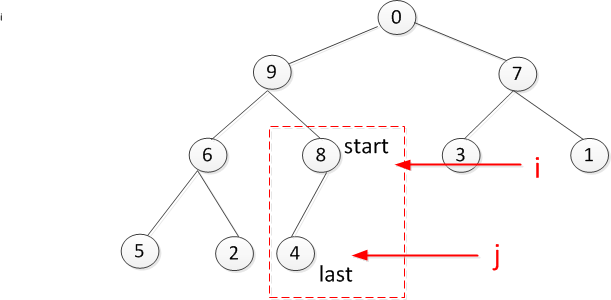
构建堆时是从最后一个叶子节点4开始，此时sift调整4，8的大小顺序，调整后接着循环，看叶子节点6是否符合要求

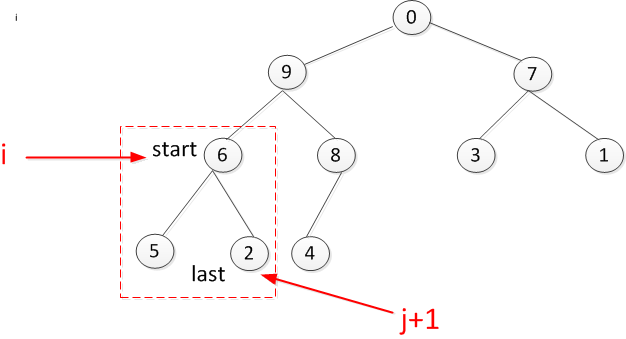
接着是叶子节点7是否符合要求

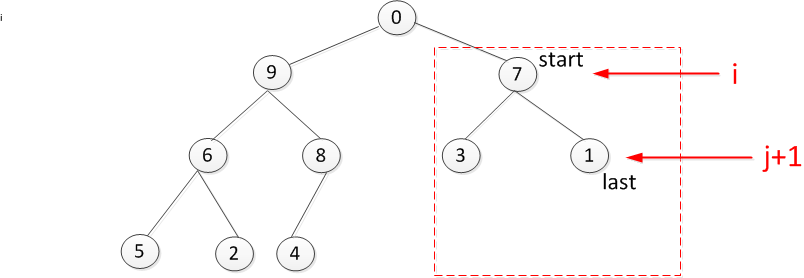
叶子节点9是否符合要求

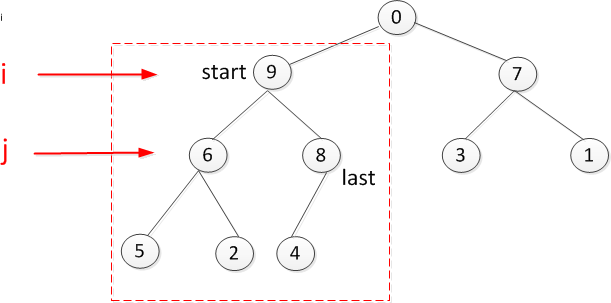
最后是根节点

这样就完成了堆排序的构建以及调整了，剩下的就是出数了，此时无须另外开辟空间，就在对结构的基础上进行就可以了，如下是调整后的堆：

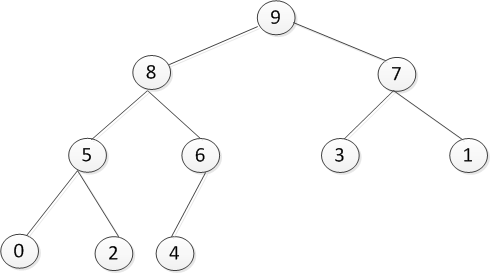
出数是首先将最后的4拿出来，然后将将顶部的9补上

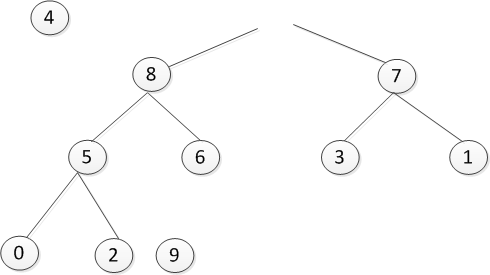
很明显4放不上，还需要进行调整，如下图所示：

每一个都是如此，最后的结果就是这样的：

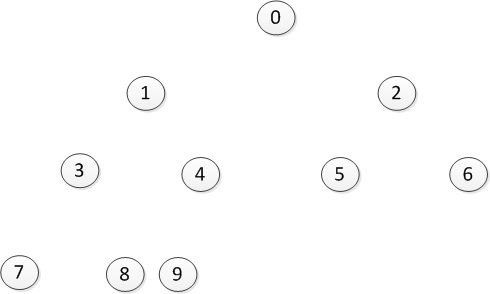
这就完成最终的出数，到此堆排序就完成了。

上面构造的是大顶堆，如果构建小顶堆，只需要修改sift函数的两个地方即可：

... 
while j <= last:  # 退出循环条件：当前位置是叶子节点，j的位置超过了last
        if j + 1 <= last and li[j + 1] < li[j]:
            j = j + 1  # 如果右边的孩子更大，j就选择右边孩子
        if temp > li[j]:
            li[i] = li[j]
            i = j
...

3、python内置堆排序

python已经有现成的堆排序，可以直接使用。

import heapq
li = [12, 58, 69, 2, 0, 5, 4, 3, 56]
heapq.heapify(li) #将列表中的数据转化为一个堆
print(li)#[0, 2, 4, 3, 58, 5, 69, 12, 56]
ln=heapq.nsmallest(len(li),li)
print(ln)#[0, 2, 3, 4, 5, 12, 56, 58, 69]

三、topK问题

现在有n个数，设计算法，找出前k大的数（k<n）

 1、解决思路

• 取列表前k各元素，组成小顶堆，堆顶就是目前第k大的元素
• 依次遍历原列表后面的元素，如果元素小于堆顶元素，则忽略该元素；如果大于堆顶元素，则将堆顶更换为该元素，并且对堆进行一次调整
• 遍历列表剩余的所有元素后，倒序弹出堆项

只需要在上面的heapSort方法中，出数之前进行堆顶元素的置换以及堆的调整，此时heapSort方法除了传入这个序列，还需要传入k

 

2、利用python内置heapq

import heapq
import random
li=list(range(100))
random.shuffle(li)
lm=heapq.nlargest(10,li)
print(lm)#[99, 98, 97, 96, 95, 94, 93, 92, 91, 90]

归并排序

希尔排序

桶排序

基数排序

计数排序

散列表

广度优先搜索

狄克斯特拉算法

贪婪算法

动态规划

K最近邻算法

参考

https://www.cnblogs.com/shenjianping/p/11069967.html