聚类分析(Cluster Analysis)
一、聚类分析与判别分析
• 判别分析:已知分类情况,将未知个体归入正确类别
• 聚类分析:分类情况未知,对数据结构进行分类
二、Q型和R型 聚类
Q型是对样本进行分类处理,其作用在于:
1.能利用多个变量对样本进行分类
2.分类结果直观,聚类谱系图能明白、清楚地表达其数值分类结果
3.所得结果比传统的定性分类方法更仔细、全面、合理
R型是对变量进行分类处理,其作用在于:
1.能够了解变量间及变量组合间的亲疏关系
2.能够依据变量的聚类结果及它们之间的关系,选择主要变量进行回归分析或Q型聚类分析
三、聚类过程
1.数据预处理(标准化)
2.构造关系矩阵(亲疏关系的描写叙述)
3.聚类(依据不同方法进行分类)
4.确定最佳分类(类别数)
3.1标准化:
3.1.1为什么要做标准化: 指标变量的量纲不同或数量级相差非常大,为了使这些数据能放到一起加以比較,常需做变换。
3.1.2相关说明:如果有N个样本1,2,…n,每一个样本有m项指标x1,x2,…,xm,用xij表示第i个样品第j个指标的值,则可得到样品数据矩阵。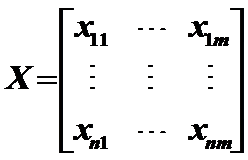
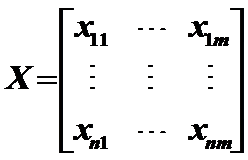
均值表示为,标准差为
,极差为
3.1.3 经常用法
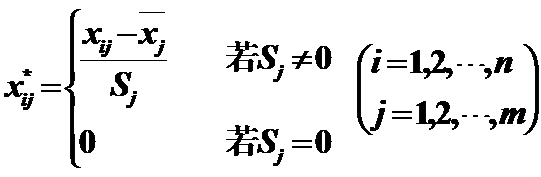
1)Z Scores:标准化变换
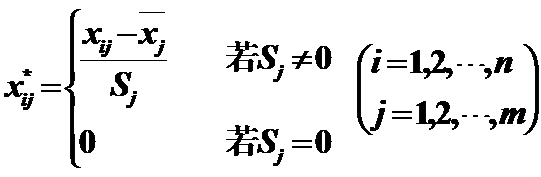
作用:变换后的数据均值为0,标准差为1,消去了量纲的影响;当抽样样本改变时,它仍能保持相对稳定性。
2)Range –1 to 1:极差标准化变换
作用:变换后的数据均值为0,极差为1,且|xij*|<1,消去了量纲的影响;在以后的分析计算中能够降低误差的产生。
3)Maximum magnitude of 1
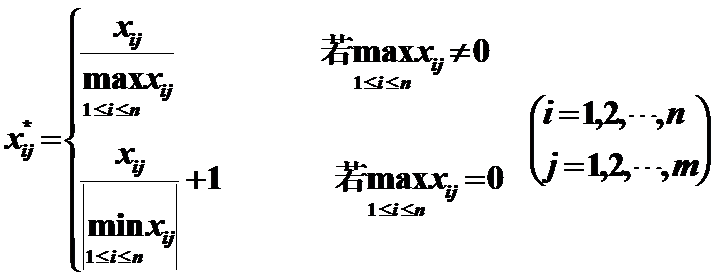
作用:变换后的数据最大值为1。
4)Range 0 to 1(极差正规化变换 / 规格化变换)

作用:变换后的数据最小为0,最大为1,其余在区间[0,1]内,极差为1,无量纲。
5)Mean of 1
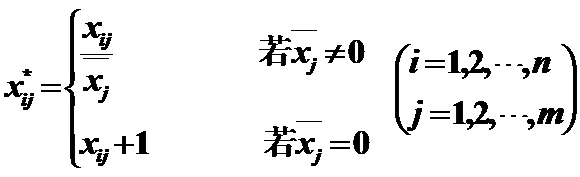
作用:变换后的数据均值为1。
6)Standard deviation of 1
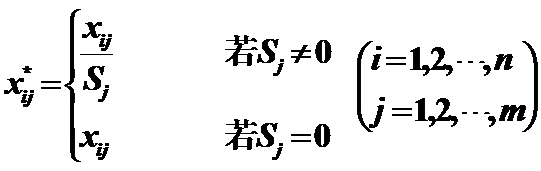
作用:变换后的数据标准差为1。
3.2构造关系矩阵
3.2.1描写叙述变量或样本的亲疏程度的数量指标有两种:
Ø相似系数——性质越接近的样品,相似系数越接近于1或-1;彼此无关的样品相似系数则接近于0,聚类时相似的样品聚为一类
Ø距离——将每个样品看作m维空间的一个点,在这m维空间中定义距离,距离较近的点归为一类。
3.2.2距离定义方式:
l)欧氏(Euclidean)距离
用途:聚类分析中用得最广泛的距离
但与各变量的量纲有关,未考虑指标间的相关性,也未考虑各变量方差的不同
2)切比雪夫(Chebychev)距离
3)明氏(Minkowski)距离
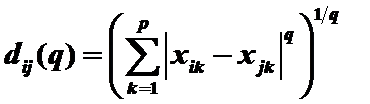
4)夹角余弦
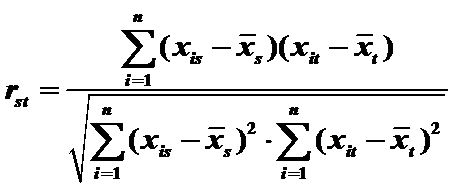
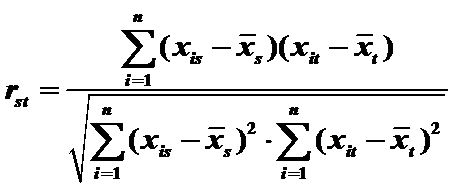
用途:计算两个向量在原点处的夹角余弦。当两夹角为0o时,取值为1,说明极相似;当夹角为90o时,取值为0,说明两者不相关。
取值范围:0~1
5)Pearson相关系数
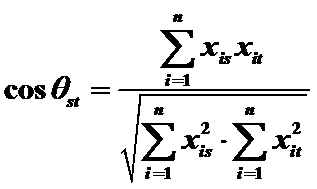
6)Block:绝对值距离(一阶Minkowski度量)
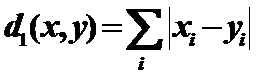


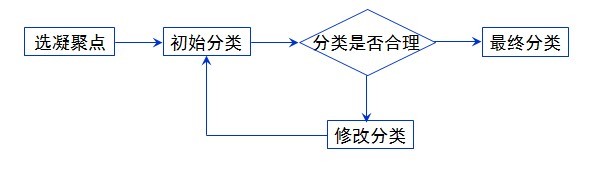
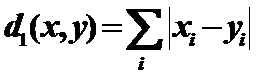
3. 选择聚类方法
1)系统聚类法(又称谱系聚类,实际应用中使用最多)。
2) 调优法(如动态聚类法)
3)模糊聚类、图论聚类、聚类预报等。
3.1系统聚类法
3.1.1系统聚类法的基本思想:令n个样品自成一类,计算出相似性測度,此时类间距离与样品间距离是等价的,把測度最小的两个类合并;然后依照某种聚类方法计算类间的距离,再按最小距离准则并类;这样每次降低一类,持续下去直到全部样品都归为一类为止。聚类过程可做成聚类谱系图(Hierarchical diagram)。
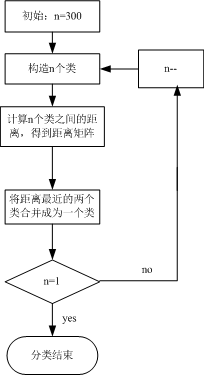
3.1.2步骤:
s1.构造n个类,每一个类包括且仅仅包括一个样品。
s2.计算n个样品两两间的距离,构成距离矩阵,记作D0。
s3.合并距离近期的两类为一新类。
s4.计算新类与当前各类的距离。若类的个数等于1,转到步骤(5),否则回到步骤(3)。
s5.画聚类图。
s6.决定类的个数,及各类包括的样品数,并对类作出解释。

3.1.3 方法:
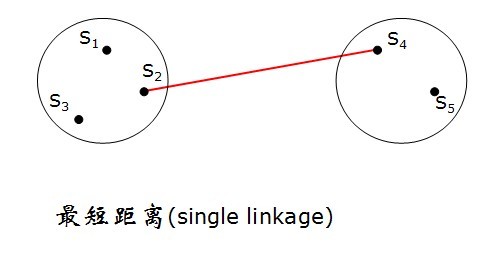
l最短距离法(single linkage)
l最长距离法(complete linkage)
l中间距离法(median method)
l可变距离法(flexible median)
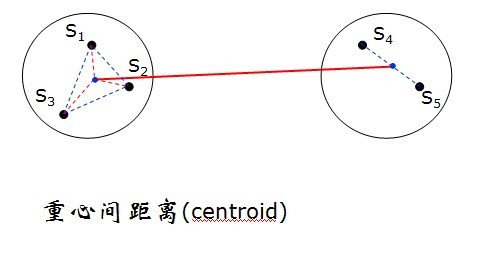
l重心法(centroid)
l类平均法(average)
l可变类平均法(flexible average)
lWard最小方差法(Ward’s minimum variance)
a)Between-groups linkage 组间平均距离连接法
方法简述:合并两类的结果使全部的两两项对之间的平均距离最小。(项对的两成员分属不同类)
b)Within-groups linkage 组内平均连接法
方法简述:两类合并为一类后,合并后的类中全部项之间的平均距离最小
c)Nearest neighbor 近期邻法(最短距离法)
方法简述:首先合并近期或最相似的两项
特点:样品有链接聚合的趋势,这是其缺点,不适合一般数据的分类处理,除去特殊数据外,不提倡用这样的方法。
d)Furthest neighbor 最远邻法(最长距离法)
方法简述:用两类之间最远点的距离代表两类之间的距离,也称之为全然连接法
e)Centroid clustering 重心聚类法
方法简述:两类间的距离定义为两类重心之间的距离,对样品分类而言,每一类中心就是属于该类样品的均值
特点:该距离随聚类地进行不断缩小。该法的谱系树状图非常难跟踪,且符号改变频繁,计算较烦。
f)Ward’s method 离差平方和法
方法简述:基于方差分析思想,假设分类合理,则同类样品间离差平方和应当较小,类与类间离差平方和应当较大
特点:实际应用中分类效果较好,应用较广;要求样品间的距离必须是欧氏距离。




3.2高速聚类
3.2.1方法:

四、谱系分类的确定
分类准则:
A.不论什么类都必须在临近各类中是突出的,即各类重心间距离必须极大
B.确定的类中,各类所包括的元素都不要过分地多
C.分类的数目必须符合有用目的
D.若採用几种不同的聚类方法处理,则在各自的聚类图中应发现同样的类
学习小结:
聚类的关键:
1)用什么指标(变量)表达要分析的样品?
2)标准化方法
3)选择聚类方法
4)用什么统计量(距离、相似系数)描写叙述样本间的相似程度?
5)用什么方法(类间距离等)进行聚类?
6)分成几类比較合适?