原题链接: http://oj.leetcode.com/problems/unique-binary-search-trees/
这道题要求可行的二叉查找树的数量,事实上二叉查找树能够随意取根,仅仅要满足中序遍历有序的要求就能够。从处理子问题的角度来看,选取一个结点为根,就把结点切成左右子树,以这个结点为根的可行二叉树数量就是左右子树可行二叉树数量的乘积,所以总的数量是将以全部结点为根的可行结果累加起来。写成表达式例如以下:
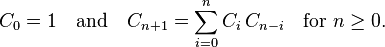
这道题要求可行的二叉查找树的数量,事实上二叉查找树能够随意取根,仅仅要满足中序遍历有序的要求就能够。从处理子问题的角度来看,选取一个结点为根,就把结点切成左右子树,以这个结点为根的可行二叉树数量就是左右子树可行二叉树数量的乘积,所以总的数量是将以全部结点为根的可行结果累加起来。写成表达式例如以下:
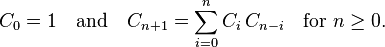
熟悉卡特兰数的朋友可能已经发现了,这正是卡特兰数的一种定义方式,是一个典型的动态规划的定义方式(依据事实上条件和递推式求解结果)。所以思路也非常明白了,维护量res[i]表示含有i个结点的二叉查找树的数量。依据上述递推式依次求出1到n的的结果就可以。
时间上每次求解i个结点的二叉查找树数量的须要一个i步的循环,整体要求n次,所以总时间复杂度是O(1+2+...+n)=O(n^2)。空间上须要一个数组来维护,而且须要前i个的全部信息,所以是O(n)。代码例如以下:
假设是求解全部满足要求的二叉树(而不不过数量)那么时间复杂度是就取决于结果的数量了,不再是一个多项式的解法了,有兴趣的朋友能够看看Unique Binary Search Trees II。
时间上每次求解i个结点的二叉查找树数量的须要一个i步的循环,整体要求n次,所以总时间复杂度是O(1+2+...+n)=O(n^2)。空间上须要一个数组来维护,而且须要前i个的全部信息,所以是O(n)。代码例如以下:
public int numTrees(int n) {
if(n<=0)
return 0;
int[] res = new int[n+1];
res[0] = 1;
res[1] = 1;
for(int i=2;i<=n;i++)
{
for(int j=0;j<i;j++)
{
res[i] += res[j]*res[i-j-1];
}
}
return res[n];
}这样的求数量的题目一般都easy想到用动态规划的解法,这道题的模型正好是卡特兰数的定义。当然这道题还能够用卡特兰数的通项公式来求解,这样时间复杂度就能够减少到O(n)。由于比較直接,这里就不列举代码了。假设是求解全部满足要求的二叉树(而不不过数量)那么时间复杂度是就取决于结果的数量了,不再是一个多项式的解法了,有兴趣的朋友能够看看Unique Binary Search Trees II。