这类题最多的就是关于灯的,像一个点控制周围点的亮灭情况,要求最小的方案数之类的,例题:
算法进阶很典型的例题,相信这道题大家都不陌生,那让我们回忆一下探索的过程,首先我们找到了倒数第二层的灯要想被点亮,且不改变这一层其他灯的情况下,只能由下一层正下方的灯实现。这样就找到l普遍的规律,即第i层如果有灯为0,想要只改变它的状态而不影响其他点的状态,可以用下方的点实现,至于第一层,可以枚举一下可能的所有状态。这个无私思路的题就解决了.
想一下我们为什么要从最后几层找规律?
因为他们位于表格的边缘,改变的话没有那么复杂,便于我们找到需要的规律...
下一题:

这个题的状态有点类似,只不过是在树上,而且一个点可以将与它相连的所有点照亮,似乎有点难办...
让我们以刚才的思路思考一下,在树的叶节点找规律.
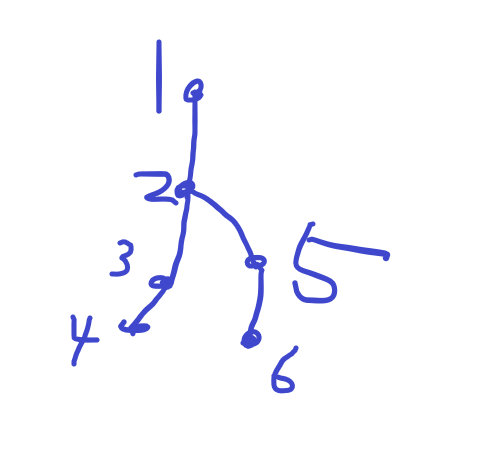
如图:4,6为叶节点,假如说想将4节点点亮有哪种方法?可以直接点亮4,也可以点亮4的父亲,3号。比较一下这两种策略,明显点亮4节点的父亲更优秀.
然后怎么办呢,我们可以这样想,反正4号迟早是要被点亮的,而点亮4的方法就这两种,最优策略肯定选能够给整体带来更大好处的策略。也就是说叶节点选择点亮父亲一定是最优的.
这样我们就可以推广到其他节点,每次点亮叶节点的父亲后,将周围的点标记后,再找出除了这些节点外的叶节点,重复操作。其实也不难想,同理,
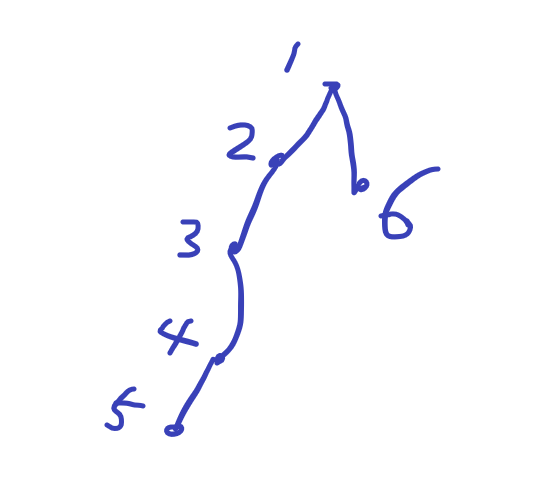
例:我们先将4点亮,这样3,4,5都标记了,此时的“叶节点”就变成了了2,对于2来说,它虽然有儿子,但儿子已经点亮,和处理5号节点时的情况一样,儿子不需要考虑,相当于没有儿子,这是想点亮它只有两种选择,点亮2或1,同理,选择他的父亲1更优秀...
这样这个题就没问题了,我当初思考时看到了叶节点要点亮父亲更优秀,但没往上扩展...
关于这类问题做个总结,要从最后找规律,因为最后的状态情况少,以与分析,之后一层层往上推就行了.
对于思考的方向做个建议:假如说找到了规律,及时它只适用于个别情况,但别放弃,尝试将这种规律普及,以及如何将其他情况变成这种情况,好了,就这吧!