概率有向图又称为贝叶斯网络,概率无向图又称为马尔科夫网络。具体地,他们的核心差异表现在如何求 ,即怎么表示
这个的联合概率。
概率图模型的优点:
- 提供了一个简单的方式将概率模型的结构可视化。
- 通过观察图形,可以更深刻的认识模型的性质,包括条件独立性。
- 高级模型的推断和学习过程中的复杂计算可以利用图计算来表达,图隐式的承载了背后的数学表达式。
一、概率有向图
对于有向图模型,这么求联合概率:
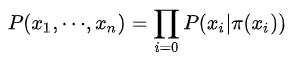
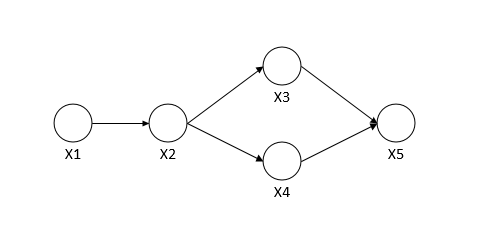
例如下图的联合概率表示如下:
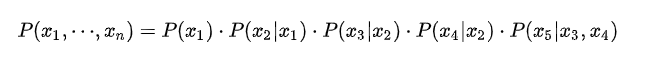
二、概率无向图
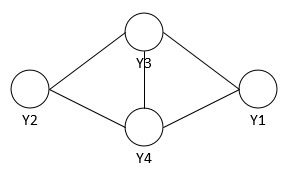
如何求解其联合概率分布呢?
将概率无向图模型的联合概率分布表示为其最大团上的随机变量的函数的乘积形式的操作,称为概率无向图模型的因子分解(factorization)。
团:无向图中任何两个节点均有边连接的节点子集。
最大团:若C为无向图G中的一个团,并且不能再加进任何一个G的节点时其成为一个更大的团,则称此团为最大团。上图中{Y2,Y3,Y4}和{Y1,Y3,Y4}都是最大团。
概率无向图模型的联合概率分布P(Y)可以表示为如下形式:
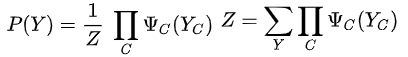
其中C是无向图最大团,Yc是C的节点对应的随机变量,是一个严格正势函数,乘积(因式分解)是在无向图所有最大团上进行的,Z是归一化因子,保证P(Y)最后构成一个概率分布。
三、条件随机场(conditional random field)
虽然定义里面没有要求,我们还是默认X和Y结构一致,这是general CRF。然后看看linear chain CRF,线性链就是X和Y都是一串序列。
linear chain CRF的公式如下:
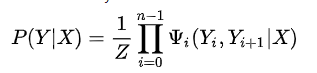
再详细一些如下:
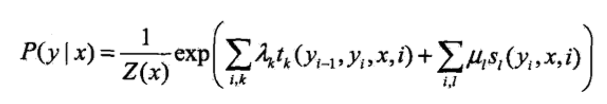
t和s都是特征函数,一个是转移特征,一个状态特征,x=(x1,x2,...,xn)为观察变量,y=(y1,y2,...,yn)为隐含变量。所以,CRF也就是直接预测p(y|x),属于判别式模型。注意一个细节,特征函数里面的观测变量为x,而不是xi,这也就是说你可以前后随意看观测变量,所以特征模板里面可以随意定义前后要看几个观测值。
亦或表示如下:
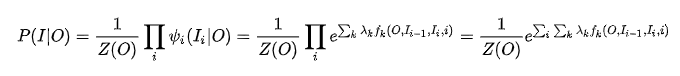
O为观察序列,I为预测的隐变量序列。
四、模型训练与运行
1)训练
CRF模型的训练主要训练特征函数的权重参数λ,一般情况下不把两种特征区别的那么开,合在一起如下:
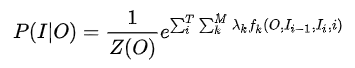
每个token会对应多个特征函数,特征函数f取值为0或者1,在训练的时候主要训练权重λ,权重为0则没贡献,甚至你还可以让他打负分,充分惩罚。利用极大似然估计寻找最优参数解。
2)工作流程
模型的工作流程:
- step1. 先预定义特征函数
,
- step2. 在给定的数据上,训练模型,确定参数
- step3. 用确定的模型做
序列标注问题或者序列求概率问题
3)序列标注
还是跟HMM一样的,用学习好的CRF模型,在新的sample(观测序列 )上找出一条概率最大最可能的隐状态序列
。
只是现在的图中的每个隐状态节点的概率求法有一些差异而已,正确将每个节点的概率表示清楚,路径求解过程还是一样,采用viterbi算法