VIS RAYTRACING

理解BRDF:

BRDF 就是最直观的描述 你camera ray(wo) 与 light ray(wi) 在 一个表面上P点 的关系。

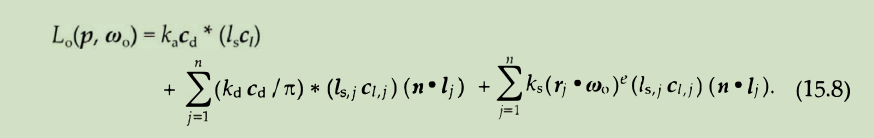
 最后一项即是对phong材质的贡献。可以理解为phong高光。

phong:

修正的高光色: 其实就是cs =  cd

 

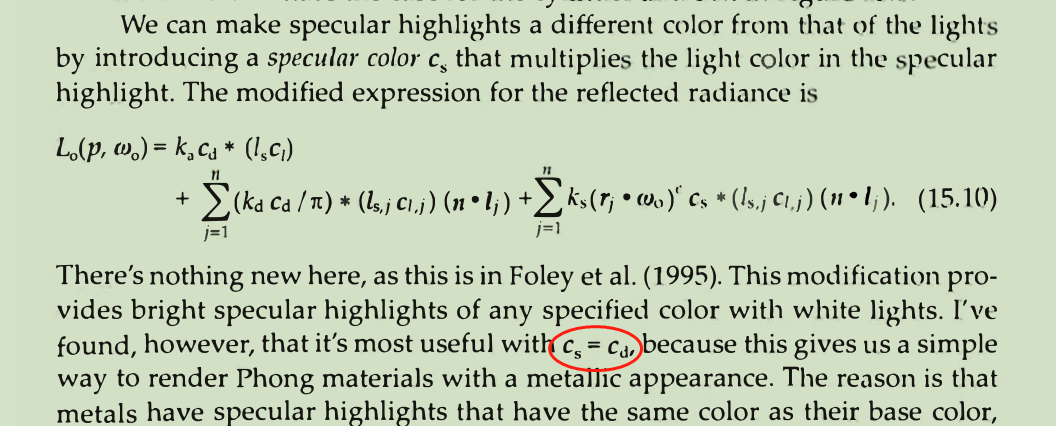
Blinn BRDF也比较简单，直接抛弃r向量了:

加入点阴影和 PHONG：

OCC:

occ里最重要的是这个可见项怎么构造。

剩下的就是个在每个ray_hit point 构造一个正交基，然后将半球采样点通过正交基 线性组合 得出方向dir,这个dir将会是shadow_ray的方向。

书中的制作是放到灯光上。也就是灯光occ,这个方法牛逼在渲染器上的pixel samples 就可以控制occ精度.

但是由于Houdini太尼玛的灵活，直接用当前的点作为ray_hit point，直接蒙特卡罗算法走起来.....都不用ray_hit point,缺点是需要大量的点

直接在sop(材质方法)测试了下:

 

 

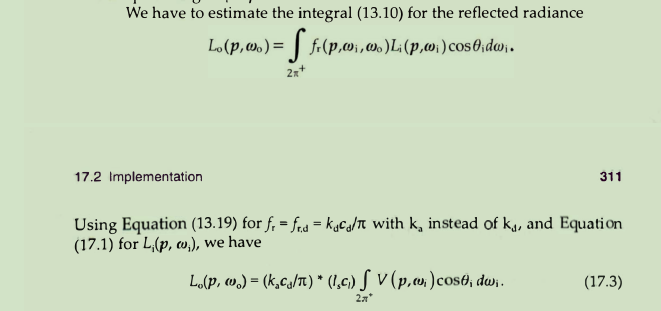
采用cos-weighted 分布的半球:

float e = chf("e");
float cos_phi = cos(2.0f * PI * @P.x); 
float sin_phi = sin(2.0f * PI * @P.x); 
float cos_theta = pow((1.0f - @P.y) , 1.0f / (e+1.0));
float sin_theta = sqrt(1.0f - cos_theta * cos_theta);
float pu = sin_theta * cos_phi;
float pv = sin_theta * sin_phi;
float pw = cos_theta;
@P.x = pu;
@P.y = pv;
@P.z = pw;

 Mirror reflection:

在这里不能用houdini的反射函数

 地面是纯颜色

 

occ + 递归镜面反射

 

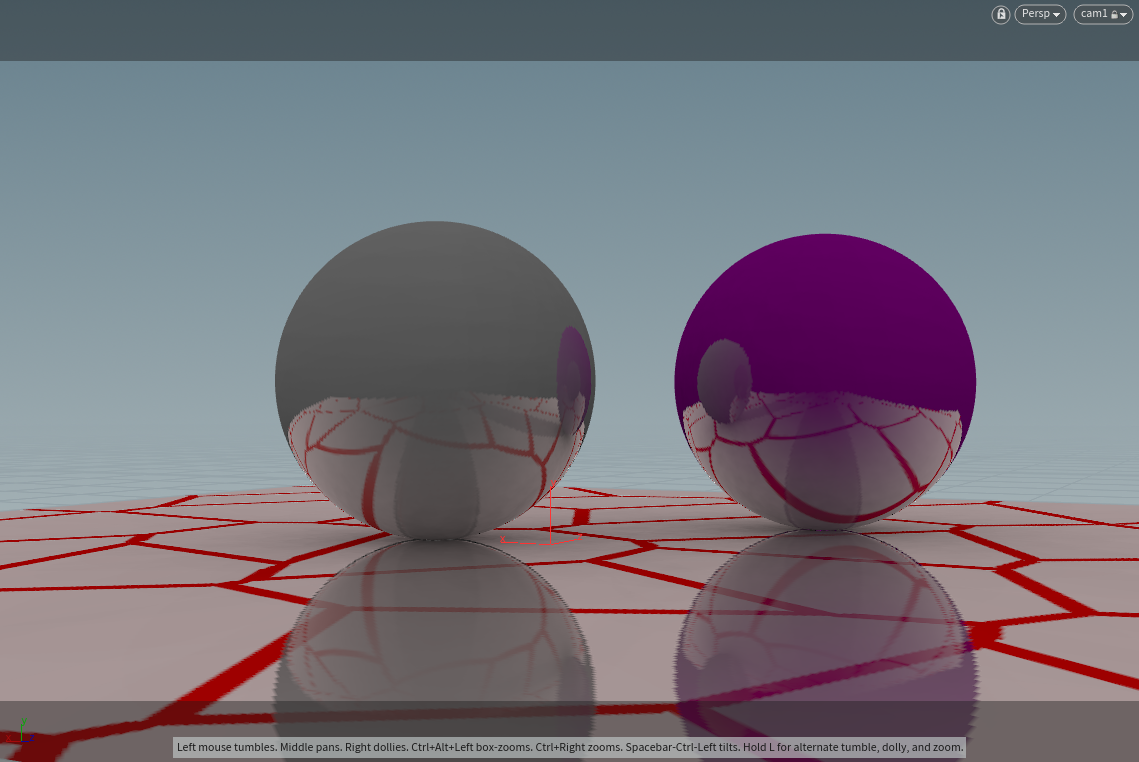
 Glossy Reflection的半球分布就是cos-weigted，但是有个问题，半球在根据ray_hit_normal 的反射向量生成时候，会造成半球进入物体内部：

vector r = point(1,"r",0);
vector getP = point(1,"P",0);

vector up = set(0,1.0f,0.0f);
vector w = r;
vector u = cross(up,w);
u = normalize(u);
vector v = cross(u,w);
v = normalize(v);

@P = getP + u*@P.x + w*@P.y + v*@P.z;

红色向量是reflect vector，有的半球点已经塞入物体了....

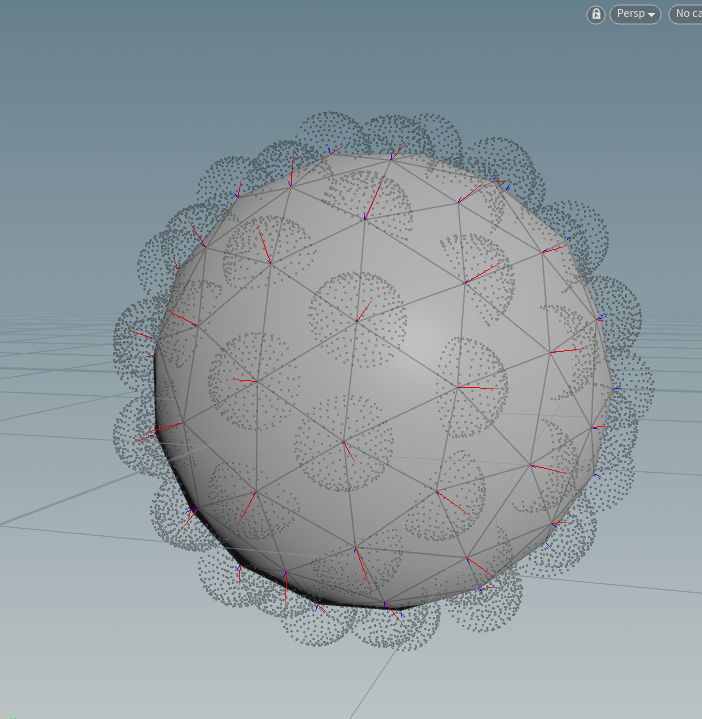
 修正方法：

vector r = point(1,"r",0);
vector getP = point(1,"P",0); // ray point P
vector getN = point(1,"N",0); // ray point N

vector up = set(0,1.0f,0.0f);
vector w = r;
vector u = cross(up,w);
u = normalize(u);
vector v = cross(u,w);
v = normalize(v);

vector wi = u*@P.x + w*@P.y + v*@P.z;

if(dot(@N,wi) >0.0f){
    wi = u * -@P.x - w * -@P.y + v* @P.z;
}

@P = getP + wi;

Area Light面积光照:

这里使用的依然不存在wo情况下制作的，假设射线的交点是@P情况下。

不过依然要模拟一个per pixel samples:

下面都是每像素采样24:

path tracing from ground up to give up:

Init 01:

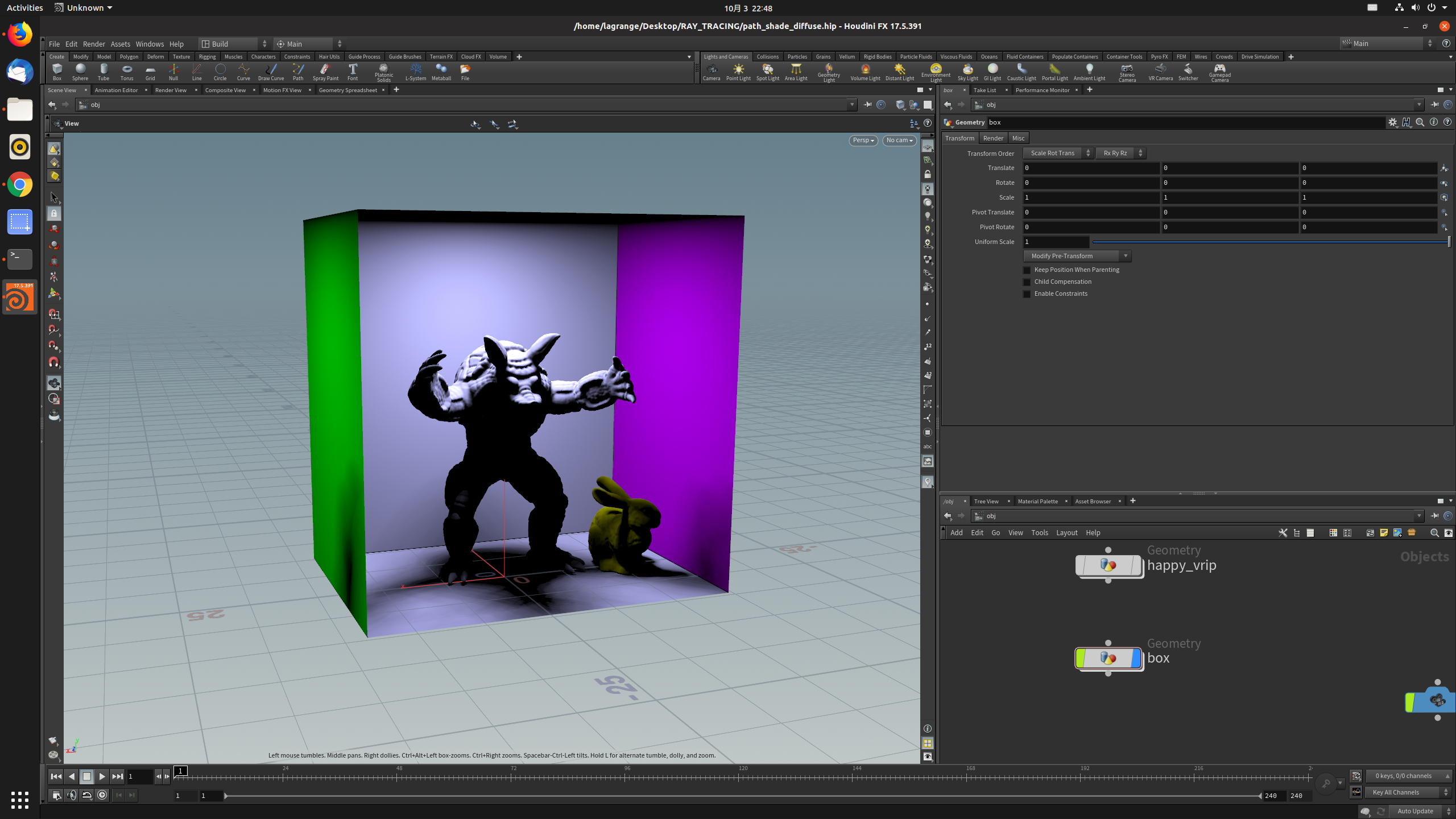
diffuse + indirect diffuse k1 + metallic reflection

ENVLightTest:

完全镜面的:采样1

均匀采样半径到0.15

0.3的半球半径无法使用普通的蒙特卡洛法收敛了:

 如果要做Diffuse BRDF 的半球基本没法。。。

1000 samples, 0.35半径，基本废，收敛太慢

IS 实现过程:

 对于一个平面上u,v其实是图像的坐标。并不是u和v在0-1区间.

那么对于一张二维图片： 1280 * 720 ,注意是sizex = 1280 sizey = 720

 

 应用这个公式，及其

float theta = 2.00f * PI  / 1280.00f * @P.x;
float phi = PI  / 720.00f * @P.y;
float r = 1.000f;
float x = r * sin(theta) * cos(phi);
float y = r * sin(theta) * sin(phi);
float z = r * cos(theta);
@P = set(x,y,z);

会得到:

一张图片球映射:

float phi = atan2(z,x) / (2 * PI);
float theta = 1 - acos(y) / PI;
float u = phi;
float v = theta;
@Cd = texture(chs("map"),u,v );

 

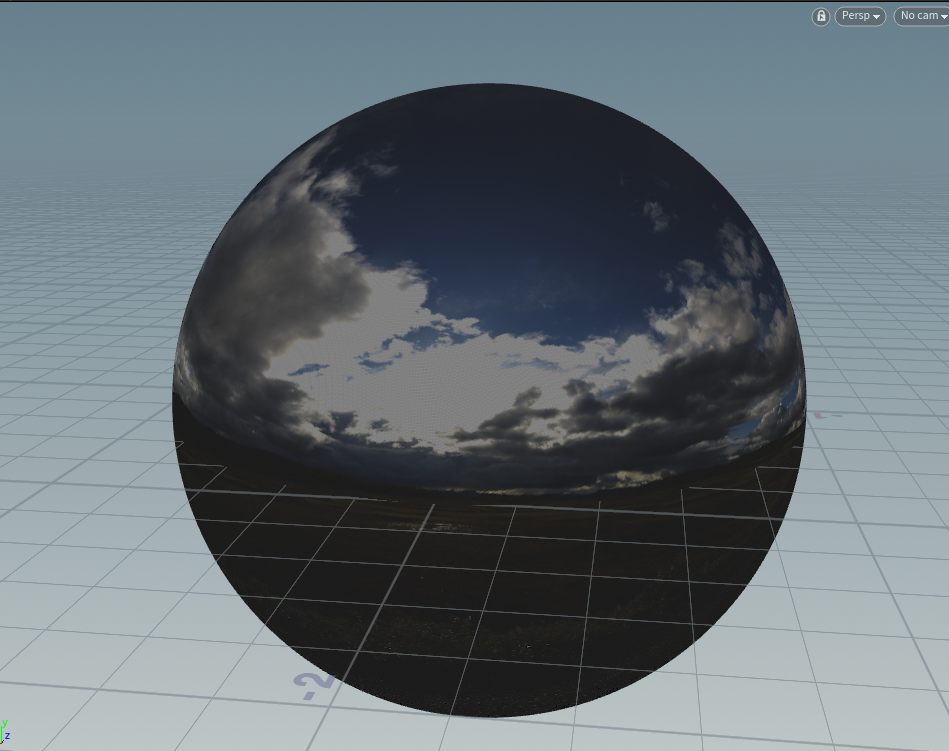
可不可爱？