Fast Control Plane Analysis Using an Abstract Representation
背景
- state-of-art verifiers 【Batfish】 are either too slow or impractical to use for proactive control plane behavior verification under arbitrary link failures
- 理论:proactive analysis tasks often require computing properties of paths, not the paths themselves
- 实际:many enterprise and data center networks use only a handful of routing protocols which interact in very specific ways
目的
(1) verifying security and availability invariants hold across arbitrary failures
(2) equivalence testing.

方法
ARC: abstract representation for control planes
- accurately model the common protocols (OSPF, RIP, and eBGP) and mechanisms (static routes, ECMP, access control lists, and route redistribution)
- is composed of a series of weighted digraphs that are routing protocol- independent.
- the true forwarding path between network locations under any failure scenario is provably included in the ARC’s digraphs, verifying key security and availability invariants boils down to computing simple graph characteristics of the ARC
network example
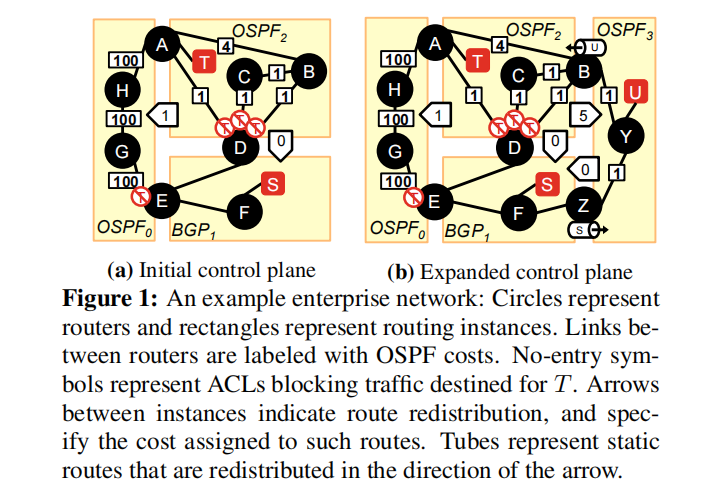
(a)的意图:由于ACL在D出接口的应用,子网S永远不能到达T
(b)的意图:子网S通过U到达T
(a)到(b)的更改,埋下了潜在隐患:当没有link failure时,数据包的路径是: F→Z→Y →B→D→A,在D这里由于ACL的存在,数据包是不可达的;但是发生link failure时,比如链路BC和BD同时断掉,则次优路径BA会发生作用,导致(a)中意图失效;
ARC structure
网络的ARC是一种数据结构,它包含一个加权有向图的集合,每个“流量类”都有一个,即一个源-目标子网对。节点表示路由进程,每个节点有in(I)和out(O),有向边数据流能够在被转发。
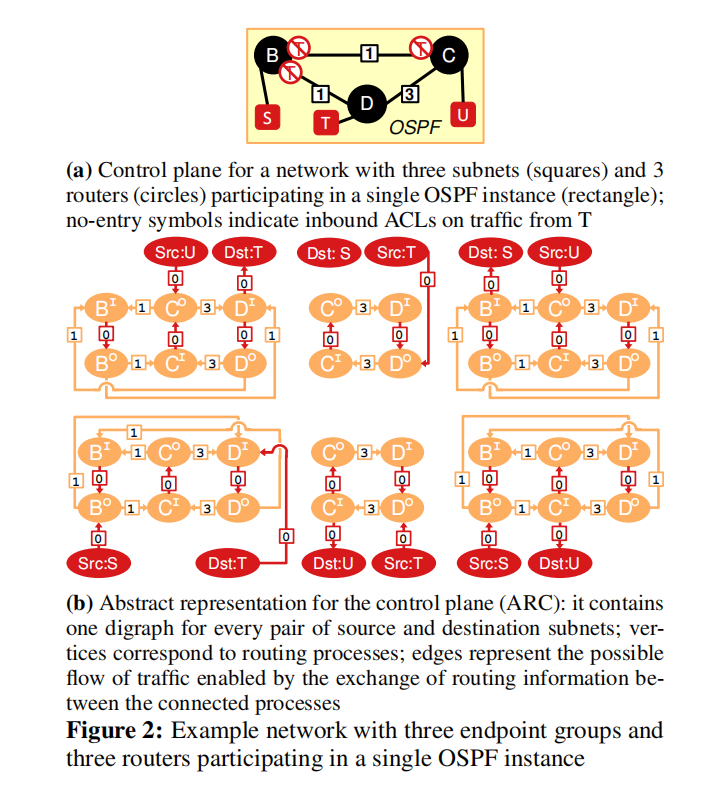
Pathset-equivalent graphs
包含在任意链路故障下,真实网络中数据包从src到dst转发所有可能的路径。
verify invariants I1–I4 in Table 1 for arbitrary link failures boils down to checking simple graph attributes.
例如要验证“子网T永远不能到达子网S或U"这个性质,只需要让T和S或U在任意故障下,始终存在于不同的连通分量中即可成立。但是因为T和U在ARC中是存在直连关系的(图2b中下方),所以上述性质可能会不成立。
Path-equivalent graphs
对ARC中的有向图各条边调整权值,使得发生链路故障时,从src到dst所选择的cost最小的路径与真实网络一致
in a real ARC the weights are a function of the relative rank of specifific routing protocols, AS paths, and network links.
ETG:extended topology graph
ETG中的顶点对应于单个路由进程。有向边表示路由进程相互间和进程内的通信路径,包括物理链路和同一设备不同进程之间交换信息的路径。在路由进程上模拟转发行为会得到一个协议无关的ARC,并且可以验证数据平面的问题。
在ARC中,边上的取值由路由协议、As路径和网络链路共同决定。本文的主要难点是如何确定ARC上的点、边和权重来尽可能真实准确地对网络模型进行编码。这部分内容细节比较繁琐,感兴趣可以深入阅读论文。
ARC验证机制
I1: Always blocked
要在任意实现任意故障的情况下,通过从src节点开始遍历ETG来检查路径的存在。如果dst节点仍然未访问,则该属性保留。否则,假设ETG是Path-equivalent的,ARC提供了最短的路径作为一个反例。
I2: Always reachable with < k failures
如果src到dst至少存在k条边不相交的路径,则在k failure的情况下始终能可达。根据Menger定理,有向图中从s到d的边不相交路径的最大数等于去除分离s和d的边的最小数,因此可以利用图的分割性质。在任意无环有向图中找到边缘不相交路径的数目是NP完全问题,但在单位权图中,问题简化为计算最大流/最小割问题。
I3: Always isolated
为了考虑安全和性能,有时需要保证两个流量不能同时经过同一条链路。只有当两个流量类的ETG没有任何共同的边时,流量的隔离性才能被保证。
I4: Always traverse a waypoint
ETG中删除所有路径点节点,并检查是否存在从数据节点到数据节点的路径。如果存在这样的路径,那么流量可能会选择一些不穿越路径点的路径;我们将此路径作为反例返回。
I5:Equivalence Testing
通过检查两个控制平面的ARC是否具有相同的顶点、边和边权重来测试两个控制平面的等效性