由于网络中路由协议执行的时序不一致原因,产生了例如经典的route update racing问题,最后产生多种可能的数据平面行为,为网络的验证带来不确定性;此外,网络验证中对于K-failure问题,一些工具例如Batfish采用枚举验证的方式,对于大规模网络存在scalability问题,效率不高;因此这篇文章针对这样两个问题,设计了Hoyan这一网络验证工具。
TopoCond
在BGP路由传播过程中,用四元组((Subnet, AS Path, Nexthop, TopoCond))来表示Rib,前三个属性的含义和变化过程与常规的路由学习一致,因此(routingPolicy)和(routingSelection)其实只涉及到这三个属性. 最后一个属性(TopoCond)是一个逻辑表达式,用来记录路由更新到达当前节点所需要满足的链路状态,由一系列的(a_i)表示,如果(a_i)为true,表示(Link_i)能够传播此路由更新; 使用这种表达方式能够记录所有链路状态下的路由更新情况, 方便处理(K\_failure)和(route update racing)问题;
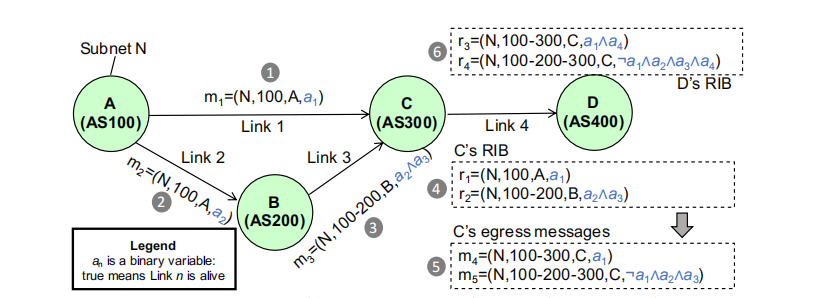
例如,在上图的例子中,每个节点在RibOut时,将当前的(TopoCond and)路由传播所经过的边(过程1,2,3);然后每个节点收到邻居发过来的路由消息后,根据路由协议,利用((Subnet, ASPath, Nexthop))路由属性计算BestRoute,同时根据同一前缀的路由优先级,按照下面公式进行更新:
含义是对于同一前缀的多条路由消息,按照路由优先级排序后,其中任一路由启用的前提条件是比它优先级更高的路由(TopoCond)不成立;此外,hoyan的方案设计里,为了验证所有可能的数据平面状态,并没有按照“接收所有邻居的路由更新,计算最优路由,并只传播最优路由”的原则来执行路由协议,而是将携带着(TopoCond)的所有路由消息都进行了传播(过程6)。
Route Update Racing
Route Update Racing是在同样的控制平面状态下,路由传播的时序不同导致不同数据平面状态的一种现象。例如下图中,A和B都要接收来自同一个子网的两台设备C和D的路由消息,并计算出最优路由再传播;
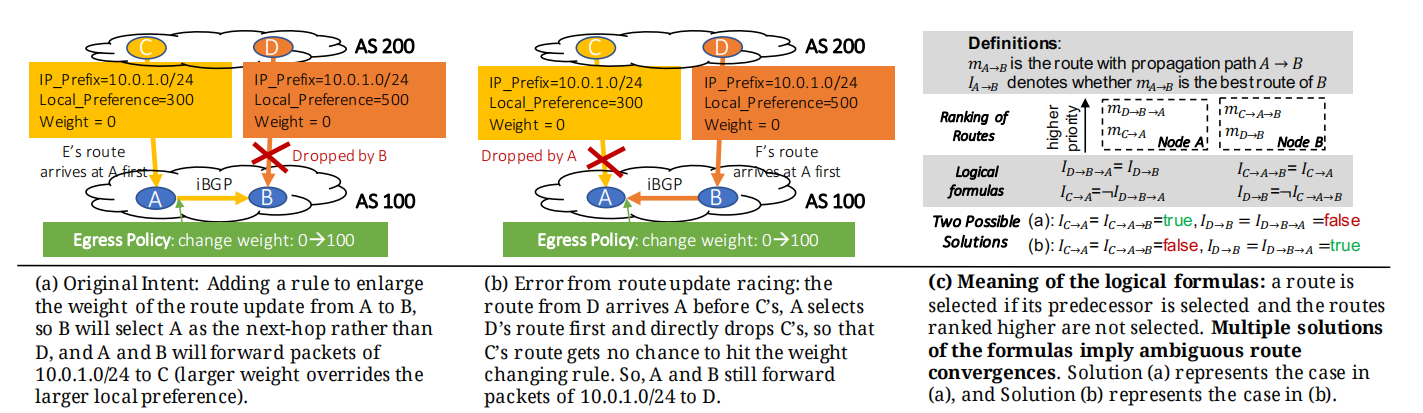
上图的例子中,C、D、A都针对前缀(10.0.1.0/24)配置了Route Map Out,不同的路由到达顺序将导致Route Map的执行结果不一样:在A处,如果C发送的Rib先于D到达,那么A处的Route Map被执行,B从A处接收的Rib将拥有更高的weight,根据优先级排序,该Rib会覆盖B从D处接收的Rib,最后A和B发往子网(10.0.1.0/24)的路由都将选择发给节点C;
另一种情况下,在A处,如果D发送的Rib先于C到达,拥有更高Local_Pref的该路由将覆盖随后从C处接收的Rib,尽管A在最优路由计算之后依然往邻居传播,A出的Route Map依然被执行,但是这条具有更高Weight的Rib由于BGP防环机制,并不会被B接收,因此,最后A和B发往子网(10.0.1.0/24)都将选择发给节点D;
传统的路由协议执行的结果无法覆盖上述两种情形,hoyan里保留了所有路径传播下的Rib,根据对这些Rib的路径信息进行编码,通过SAT求解找到所有成立的结果;
K-failure
K-failure问题是假设网络中最多出现K条链路故障的条件下,网络属性是否依然成立的一类问题;基于上述内容,通过判断保留Rib的TopoCond的K-failure条件下的满足性,可以很快得到路由可达的可满足性。具体来说,由于保留了所有带有(TopoCond)的Rib, 对于某个节点去往某个前缀的所有转发规则(r_i) 和这些规则里的链路状态(R(r_i)), 只需要求出逻辑表达式(R(r_1) or ... or R(r_n)=False)时,表达式中(a_i=False)的最少个数,然后和K比较就能得到Rib在K-failure下的可满足性。