Leetcode练习(Python)：数组类：第53题：给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。进阶: 如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的分治法求解。

题目：

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。进阶:  如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的分治法求解。

思路：贪心法和分而治之

程序1：贪心发

class Solution:

    def maxSubArray(self, nums: List[int]) -> int:

        length = len(nums)

        auxiliary = nums[0]

        temp_result = nums[0]

        for index in range(1,length):

            auxiliary = max(nums[index], auxiliary + nums[index])

            temp_result = max(auxiliary, temp_result)

        

        result = temp_result

        return result

程序2：分而治之

官方思路示图：

 

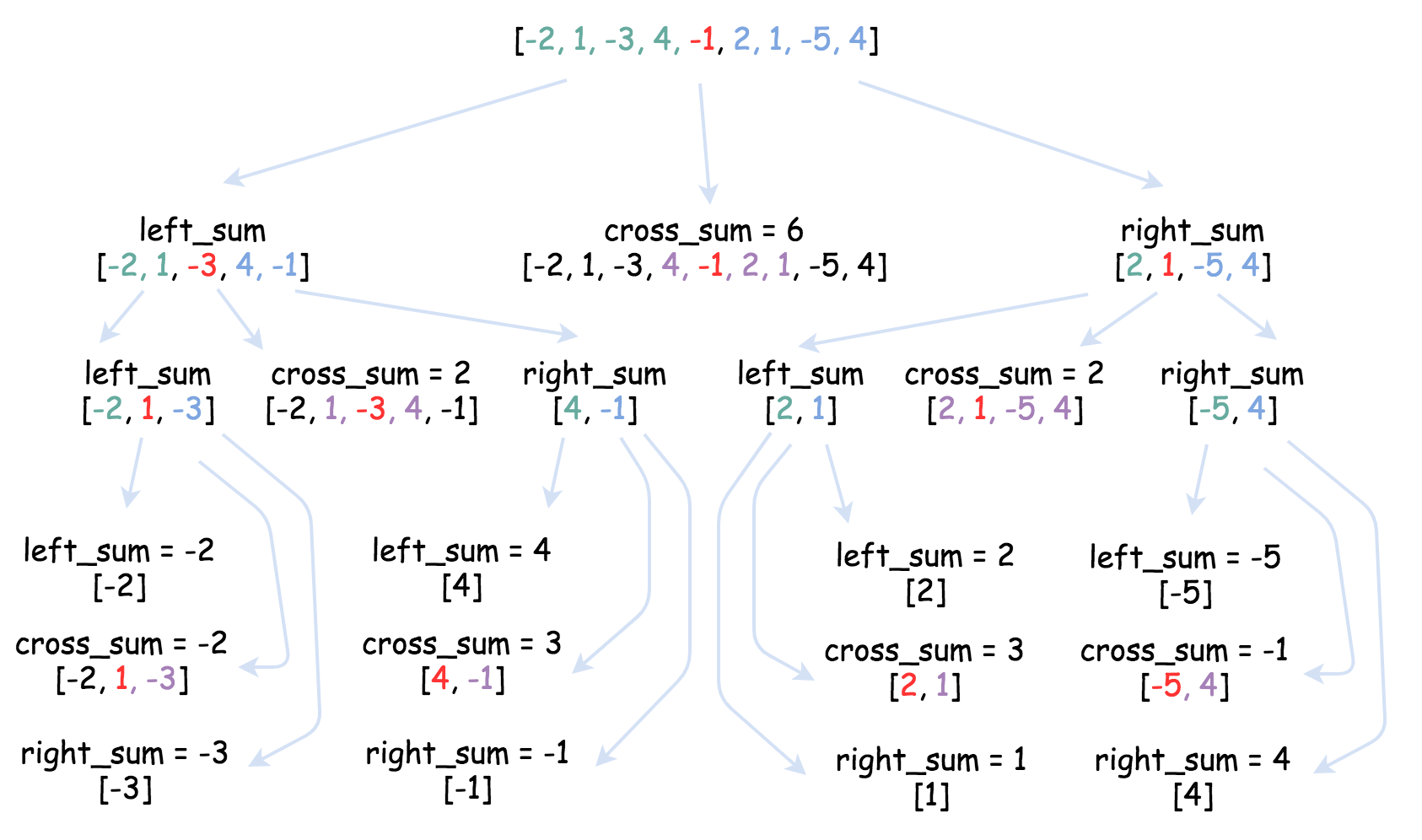
class Solution:

    def maxSubArray(self, nums: List[int]) -> int:

        length = len(nums)

        if length <= 1:

            return nums[0]

        left = self.maxSubArray(nums[0 : len(nums) // 2])

        right = self.maxSubArray(nums[len(nums) //2 : len(nums)])

        middle_left = nums[len(nums) // 2 - 1]

        auxiliary_1 = 0

        for index1 in range(len(nums) // 2 - 1, -1, -1):

            auxiliary_1 += nums[index1]

            middle_left = max(middle_left, auxiliary_1)

        

        middle_right = nums[len(nums) // 2]

        auxiliary_2 = 0

        for index2 in range(len(nums) // 2, len(nums), 1):

            auxiliary_2 += nums[index2]

            middle_right = max(middle_right, auxiliary_2)

        

        middle = middle_left + middle_right

        result = max(left, right, middle)

        return result